6.栈和队列

1.栈 Stack

1.1 栈的定义

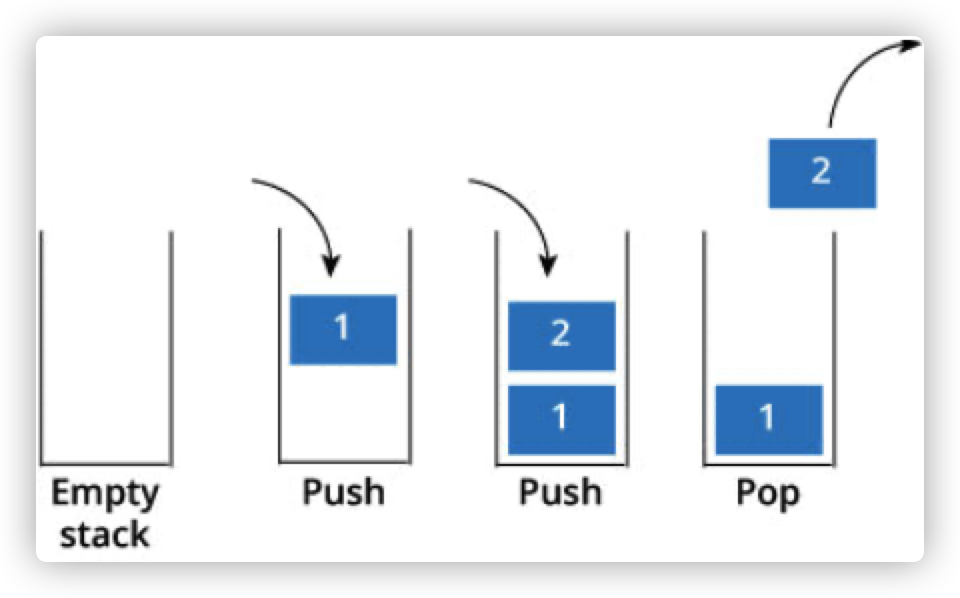
栈提供push 和 pop 等等接口，所有元素必须符合先进后出规则，所以栈不提供走访功能，也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。

栈是以底层容器完成其所有的工作，对外提供统一的接口，底层容器是可插拔的（也就是说我们可以控制使用哪种容器来实现栈的功能）。

所以STL中栈往往不被归类为容器，而被归类为container adapter（容器适配器）。

1.2 栈的应用

1.2.1括号和 HTML 匹配

1.算法描述

每次遇到一个开始符时都将其压入栈中；每次遇到一个结束符时，从栈顶弹出一个分隔符，并检查这两个分割符是否可以凑成一对。

具体题目详见：LeetCode题目链接

1.2.2 栈的现实应用

1.网页后退按钮的操作

浏览器将浏览的网页存在一个栈中，当用户浏览一个新网页时，这个网页就被压入栈顶。这样用户在点击后退按钮的时候，就会弹出刚刚访问的地址

2.文本编辑器的撤销机制

撤销机制会取消最近的编辑操作并回到最原先的文本状态

1.4 栈的底层实现

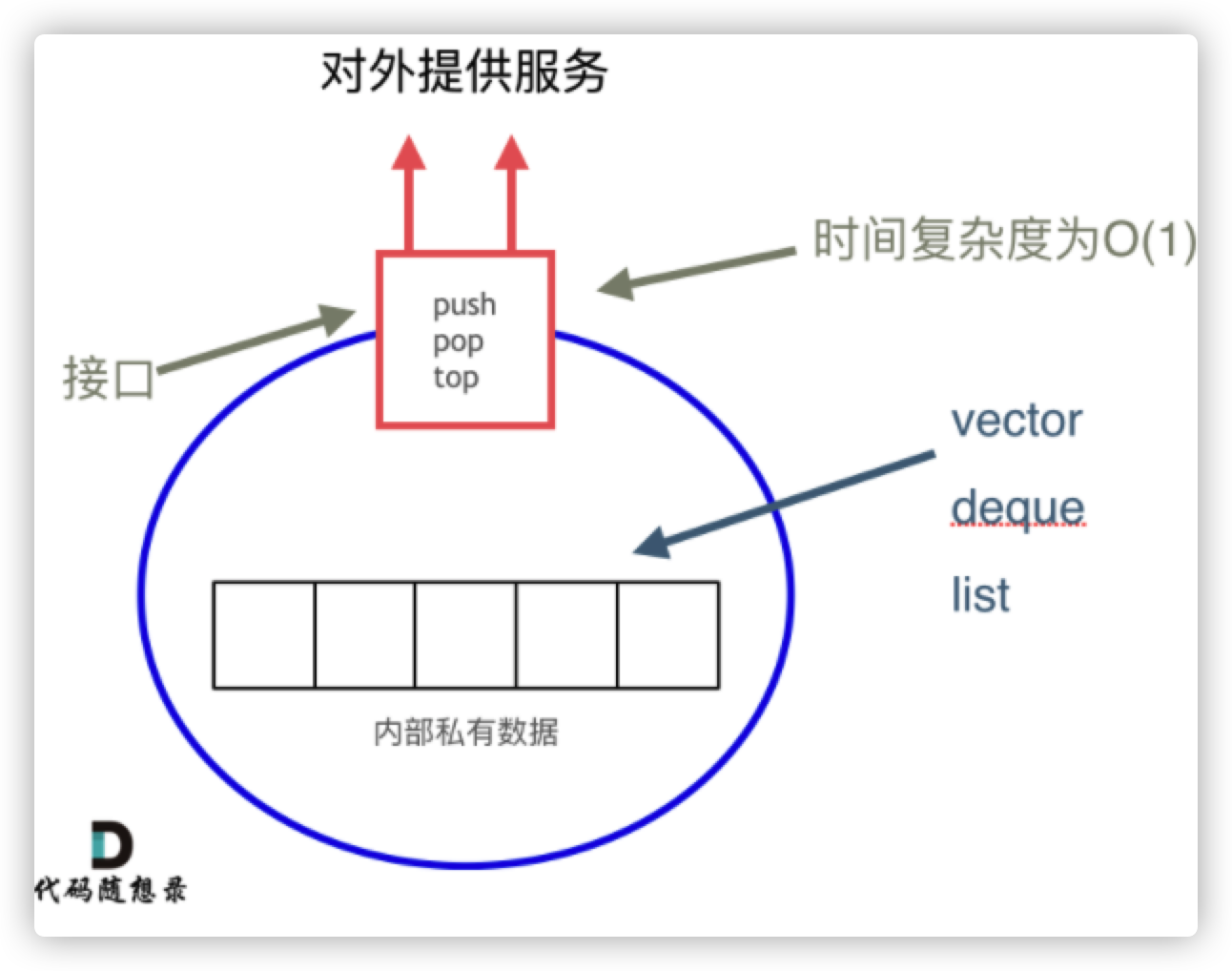
从上图中可以看出，栈的内部结构，栈的底层实现可以是vector，deque，list 都是可以的， 主要就是数组和链表的底层实现。

我们常用的SGI STL，如果没有指定底层实现的话，默认是以deque为缺省情况下栈的低层结构。

deque是一个双向队列，只要封住一段，只开通另一端就可以实现栈的逻辑了。

我们也可以指定vector为栈的底层实现，初始化语句如下：

std::stack<int, std::vector<int> > third;  // 使用vector为底层容器的栈

2.队列 queue

2.1 队列定义

队列中先进先出的数据结构，同样不允许有遍历行为，不提供迭代器, SGI STL中队列一样是以deque为缺省情况下的底部结构。

2.2 队列的应用

2.2.1 现实场景应用

1.网络打印机

2.响应 Web 请求

3.操作系统中页面置换算法

2.4.3假溢出问题

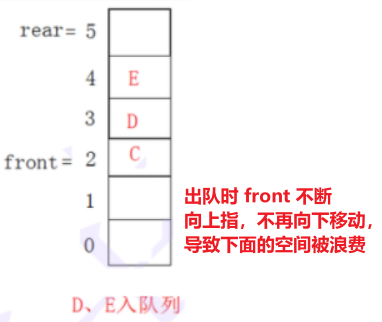
假溢出：顺序队列因多次入队和出队的操作出现尚有存储空间但是无法再进行入队操作的溢出

2.5 循环队列

上图来自百度百科。为充分利用向量空间，克服"假溢出"现象，把顺序队列首尾相连，这样存储元素的表从逻辑上看做是一个环。

2.5.1循环队列指针移动

初始化：Q.front==Q.rear==0
入队：Q.front = (Q.front+1)%Maxsize
出队：Q.rear = (Q.rear+1)%Maxsize
队长：(Q.rear+Maxsize-Q.front)%Maxsize

取模的作用就是防止 front 或者 rear 一直 +1 导致内存地址溢出，而取模可以将 front 和 rear 的值固定在 Maxsize 大小的范围

2.5.2顺序&循环队列判断队空和队满

有三种方法可以判断一个队列是空还是满

1.牺牲一个单元

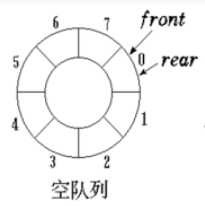
队空：Q.front==Q.rear
队满：(Q.front+1)%Maxsize==Q.rear

2.设置变量用于计数

队空：Q._size == 0
队满：Q._size == Maxsize

3.设置一个 tag 对最后一次操作进行记录

如果最后一次操作是出队操作：设置 tag=0

当 Q.front==Q.rear 且 tag=0 ，则可判断为队空

如果最后一次操作是入队操作：设置 tag=1

当 Q.front==Q.rear 且 tag=1 时，则可判断为队满

2.7双端队列（deque）

允许两端弹出一端输入的队列或者允许两端输入一段弹出的队列

双端队列同样也是使用列表实现

2.8 STL 的版本

1. HP STL 其他版本的C++ STL，一般是以HP STL为蓝本实现出来的，HP STL是C++ STL的第一个实现版本，而且开放源代码。
2. P.J.Plauger STL 由P.J.Plauger参照HP STL实现出来的，被Visual C++编译器所采用，不是开源的。
3. SGI STL 由Silicon Graphics Computer Systems公司参照HP STL实现，被Linux的C++编译器GCC所采用，SGI STL是开源软件，源码可读性甚高。

3.LeetCode 相关题目

232 使用栈描述队列

3.1.1 算法描述

栈有个非常重要的逆序操作，两个栈可以实现逆序输出，而队列就是栈的逆序输出

stack_in 的作用：输入时直接输入

stack_out 的作用：当想要操作某个数据时需要将这个数据以及其前面的数据先保存到 out 中

所有的元素想要操作都要先放入 out 中

1.pop()：将队列首部的元素删除

• 输出栈如果为空，就把进栈数据全部导入进来（注意是全部导入），再从出栈弹出数据

• 如果输出栈不为空，则直接从出栈弹出数据就可以了。

2.peek()：返回队列首部的元素

先将要操作的元素在 out 中弹出

然后再放回到 out 中

3.empty()：队列判空

两个队列都为空

4.push()：将一个元素放入队列的尾部

正常的插入到 stack_in 中

3.1.2 代码实现

1.C++ 代码实现

class MyQueue {
  public:
  stack<int> stIn;
  stack<int> stOut;
  MyQueue() {

  }
  void push(int x) {
    stIn.push(x); // 直接添加元素
  }
  int pop() {
    if(stOut.empty()){ // 如果 out 为空，则将 in 的数据全部放入 out
      while(!stIn.empty()){
        stOut.push(stIn.top());
        stIn.pop();
      }
    }
    int result = stOut.top();
    stOut.pop();
    return result;
  }
  int peek() {
    int res = this->pop(); // 调用自己的 pop 方法
    stOut.push(res);
    return res;
  }
  bool empty() {
    return stIn.empty()&&stOut.empty();
  }
};

2.Python 代码实现

class MyQueue:
    def __init__(self):
        """
        初始化 in 和 out 两个栈
        """
        self.stack_in = list()
        self.stack_out = list()
    def push(self, x: int) -> None:
        """
        输入时直接保存到 in 中
        """
        self.stack_in.append(x)
    def pop(self) -> int:
        """
        输出并移除
        """
        # 1.判空
        if self.empty():
            return None
        # 2.先看 out 中是否有存储元素，在 out 中没有元素后再从 in 中拿元素
        if self.stack_out:
            return self.stack_out.pop()
        else:
            for i in range(len(self.stack_in)):
                self.stack_out.append(self.stack_in.pop()) 
        # 4.输出 out 最上面的元素
        return self.stack_out.pop()

    def peek(self) -> int:
        if self.empty():
            return None
        # 先把这个元素弹出，然后再放入
        ans = self.pop()
        self.stack_out.append(ans)
        return ans

    def empty(self) -> bool:
        return not (self.stack_in or self.stack_out)
# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()

常见错误：

1.在 pop 方法中，stack_in 的数据要先 pop 出去

3.1.3 list 的 pop 方法

list 的 pop 方法可以移除并返回 list 最后一个元素

list pop 方法介绍

225用队列实现栈

3.2.1 算法描述

栈和队列不太一样，栈是先进后出，所以用栈实现队列会导致元素的进出顺序不一样，多所以 stOut 的作用是用来调整元素的进出顺序的。但是队列是先进先出，元素输入输出顺序不变，所以第二个队列是用来数据备份的

将 que1 的数据导出到 que2 ，将 que1 相应的元素弹出后再将 que2 的数据返还到 que1中

1.push

直接将元素入队

2.pop()：移除栈顶元素

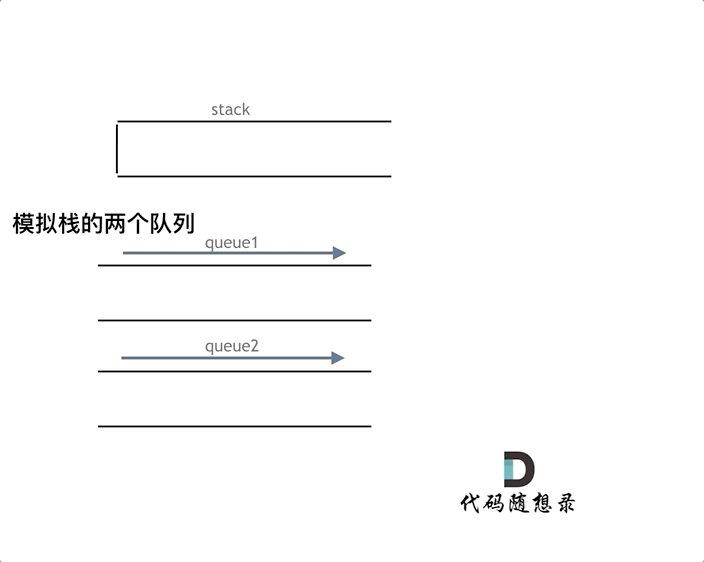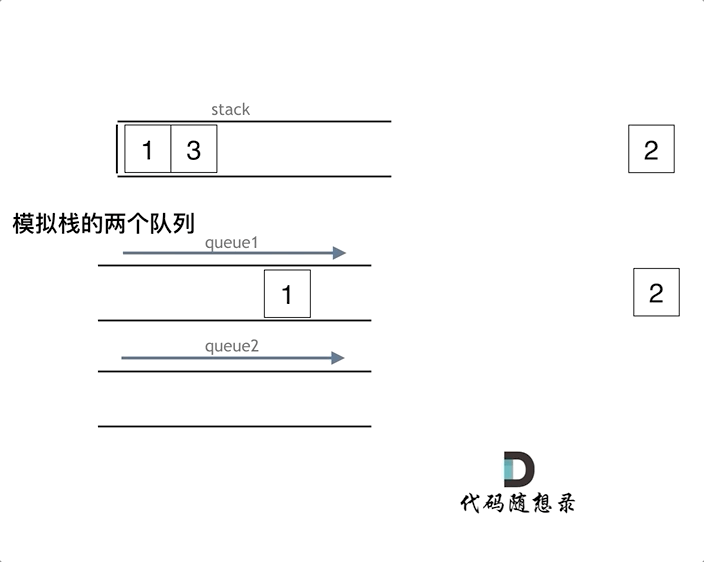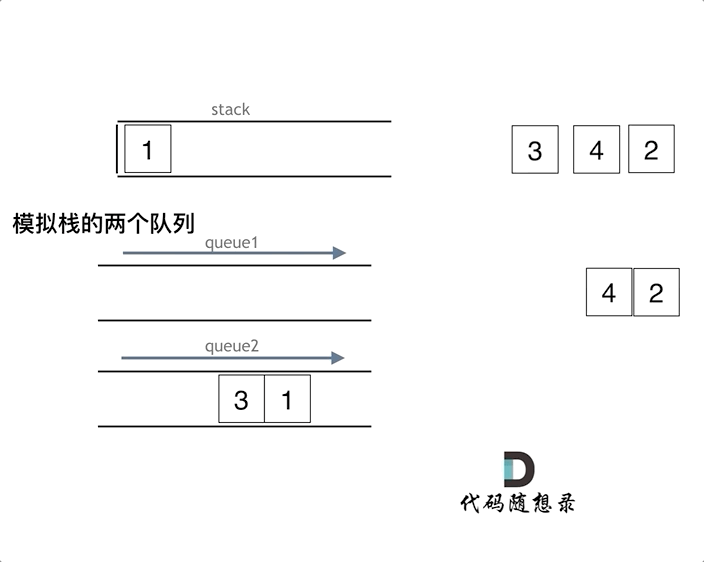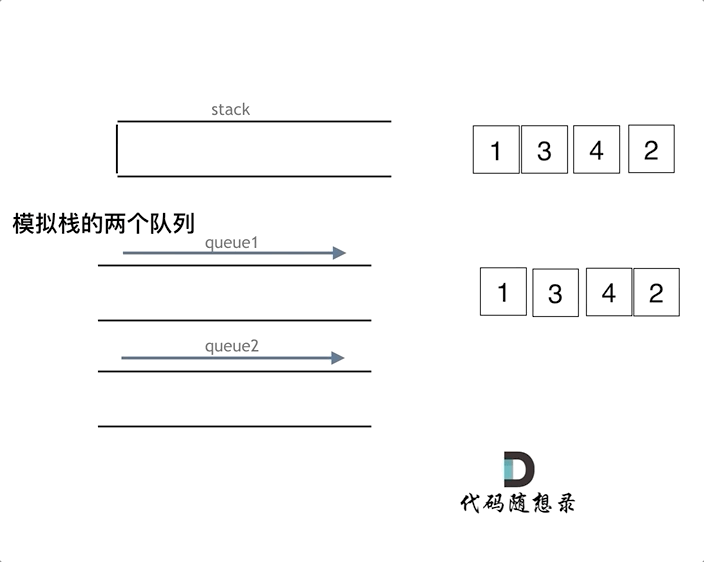
这一步包含两个操作：输出值+移除

首先将 que1 中的所有元素（除最后一个）放到 que2 中，将 que1 最后一个元素弹出

这里对 que1 遍历的方法使用的是 que1 的个数，不能用 empty() 方法，因为最后一个元素需要保存在 que1 中

再将 que2 保存的那些元素再放回到 que1 中

3.top()：获取栈顶元素

使用 pop 方法先得到最后一个元素，然后再将最后一个元素放回去

4.empty 方法

因为 out 只有数据备份作用，备份完的数据还要再返回到 in 中，所以只需要对 in 判空即可

3.2.2 代码实现

1.C++ 代码实现

class MyStack {
  public:
  queue<int> que1;
  queue<int> que2;
  MyStack() {

  }
  void push(int x) {
    que1.push(x);
  }
  int pop() {
    // 先将 que1 除最后一个元素外的所有元素放到 que2 中
    int size = que1.size();
    size--; // 最后一个元素不放
    while(size--){
      que2.push(que1.front());
      que1.pop();
    }
    int result = que1.front(); // 得到最后一个元素
    que1.pop();
    que1 = que2; // 直接赋值，不用一个个再弹出
    while(!que2.empty()){
      que2.pop();
    }
    return result;
  }
  int top() {
    return que1.back(); // que1 的队尾元素
  }
  bool empty() {
    return que1.empty();
  }
};

2.Python 代码实现

class MyStack:
    def __init__(self):
        """
        定义输入队列和备份队列,都是双端队列
        """
        self.queue_in = collections.deque()
        self.queue_out = collections.deque()
    def push(self, x: int) -> None:
        """
        添加时直接入队
        """
        self.queue_in.append(x)
    def pop(self) -> int:
        """
        移除栈顶元素，并返回
        """
        # 1.判空
        if  self.empty():
            return None
        # 2.先将 in 中 cur 之前的元素都备份到 out 中
        for i in range(len(self.queue_in)-1):
            self.queue_out.append(self.queue_in.popleft())
        # 3.将 out 中备份的元素再依次放回 in 中，即 in 和 out 交换,此时 in 中保存的元素是需要出对的元素
        self.queue_in,self.queue_out = self.queue_out,self.queue_in
        # 4.out 出队
        return  self.queue_out.popleft()
    def top(self) -> int:
        """
        Get the top element.
        """
        # 1.判空
        if self.empty():
            return None
        # 2.栈：后进先出；直接返回最后一个进队的元素,不牵扯其他元素，不用备份
        return self.queue_in[-1]
    def empty(self) -> bool:
        """
        判空
        """
        # 因为 out 队列只用于备份，备份队列的元素最终还要送回到 in 中，所以只需要判断 in
        return len(self.queue_in)==0
# Your MyStack object will be instantiated and called as such:
# obj = MyStack()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.top()
# param_4 = obj.empty()

20 有效的括号

LeetCode 题目链接

3.3.1 算法描述

1.三种不匹配的状况

（1）左括号多余

（2）括号没有多余，但是括号的类型没有匹配上

（3）右括号多余

2.遍历每个字符后的操作

括号匹配算法：

• 凡出现左括弧，则对应右括号进栈
• 凡出现右括弧，首先检查栈是否空
  若栈空，则表明该右括号多余（说明没有左括号匹配了）
  栈不为空，和栈顶元素比较
  因为栈中只有右括号，所以 cur 如果和栈顶元素不相同则返回 false
  括号相同 continue
• 表达式检验结束时
  若栈空，则表明表达式中匹配正确，
  否则表明“左括弧”有余（栈不为空说明里面有右括号，右括号是因为放入了左括号导致的）

3.3.2 代码实现

1.C++

class Solution {
  public:
  bool isValid(string s) {
    stack<int> st;
    for(int i =0;i<s.size();i++){
      if(s[i]=='(') st.push(')'); // 左括号，有括号入栈
      else if (s[i] == '{') st.push('}');
      else if (s[i] == '[') st.push(']');
      else if(st.empty()||st.top()!=s[i]) return false; // 当前子字符是右括号：栈空，栈中没有要匹配的字符
      else st.pop(); // st.top() 和 s[i] 相等，栈弹出元素
    }
    return st.empty();
  }
};

2.Python

class Solution:
    def isValid(self, s: str) -> bool:
        dic = {')':'(','}':'{',']':'['} # 定义一个相反逻辑的字典
        stack = []
        for c in s:
            if stack and c in dic.keys():
                if stack.pop() == dic[c]:
                    continue
                else:
                    return False
            else:
                stack.append(c)
        return not stack

3.3.3 时空复杂度

时间复杂度：O(N)

空间复杂度：O(N)

1047删除字符串中的所有相邻重复项(easy)

LeetCode 题目链接

3.4.1 算法描述

这道题目就像是玩过的游戏对对碰，逐渐向栈中放入元素，如果相同的元素放在挨在一起就要消除。

最后再将栈中剩余的字符串进行反转

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-I5oCPIcq-1644592254907)(/Users/xuguagua/Documents/typora_file/gif/\1047.删除字符串中的所有相邻重复项.gif)]

3.4.2 代码实现

1.C++

class Solution {
  public:
  string removeDuplicates(string S) {
    stack<char> st;
    for (char s : S) {
      if (st.empty() || s != st.top()) {
        st.push(s);
      } else {
        st.pop(); // s 与 st.top()相等的情况
      }
    }
    string result = "";
    while (!st.empty()) { // 将栈中元素放到result字符串汇总
      result += st.top();
      st.pop();
    }
    reverse (result.begin(), result.end()); // 此时字符串需要反转一下
    return result;

  }
};

2.Python

class Solution:
    def removeDuplicates(self, s: str) -> str:
        # 使用栈
        stack = list()
        for c in s:
            if stack:
                # 先判断 -1 元素和当前元素是否相同
                if stack[-1]==c:
                    stack.pop()
                else:
                    stack.append(c)
            else:
                stack.append(c)
        return ''.join(stack)

3.4.3 时空复杂度

时间复杂度：O(N)

空间复杂度：O(N)

150逆波兰表达式求值

LeetCode 题目链接

算法描述

逆波兰表达式其实就是后缀表达式，本题的要求相当于给出后缀表达式计算表达式的值

如何通过后缀表达式计算数值

通用方法：

1.遇到数字：直接入栈

2.遇到运算符：将栈顶的两个元素出栈进行计算，将结果压入栈

3.最后栈顶元素就是结果

代码实现

1.C++

class Solution {
  public:
  int evalRPN(vector<string>& tokens) {
    stack<int> st;
    for (int i = 0; i < tokens.size(); i++) {
      if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") { // 直接判断字符
        int num1 = st.top(); // 得到第一个栈顶元素
        st.pop();
        int num2 = st.top(); // 得到第二个栈顶元素
        st.pop();
        if (tokens[i] == "+") st.push(num2 + num1);
        if (tokens[i] == "-") st.push(num2 - num1);
        if (tokens[i] == "*") st.push(num2 * num1);
        if (tokens[i] == "/") st.push(num2 / num1);
      } else {
        st.push(stoi(tokens[i]));
      }
    }
    int result = st.top();
    st.pop(); // 把栈里最后一个元素弹出（其实不弹出也没事）
    return result;
  }
};

常见错误：

1.最后 stack 中保存的是 str 元素，需要将 return 的元素转换为 int

2.因为数字不在 0~9 之间，所以判断是否是数字还是比较麻烦。这里判断 s[i] 是否是字符串比较简单

2.Python

class Solution:
    def evalRPN(self, tokens: List[str]) -> int:
        stack = []
        fuhao_list = ['+','-','*','/']
        for c in tokens:
            if c not in fuhao_list:
                stack.append(c)
            else:
                a = stack.pop()
                b = stack.pop()
                res = int(eval(f'{b}{c}{a}'))
                stack.append(res)
        return int(stack[-1])

时空复杂度

时间复杂度：O(N)

空间复杂度：O(N)

Python 库实现

1.eval()

执行括号中字符串的表达式

eval() 的使用

**2.python 字符串前的 f **

使用 {} 将一个变量进行包裹，可以将这个变量转换成值

Python 字符串前添加 f

239滑动窗口最大值（hard）

算法描述

1.暴力解：

Step1：先将前 k 个元素放到队列中。

Step2：将剩余元素放到队列当中，每入队一个元素就要出队时间最长的那个元素，并且每次遍历队列的最大值，将最大值放入 res 中。

缺点：时间复杂度为 O(n*k) n 是需要遍历 nums 中的每个元素，k 是遍历滑动窗口中的每个元素

2.单调队列：

构建一个单调队列，里面的数值是从大到小进行排序的。并且在 index=0 时元素最大

每次遍历一个 nums 中的元素时都需要移除单调队列中的一个老元素，并向 que 中添加当前元素。所以一共有 pop 元素和 push 元素两个操作

（1）pop 移除元素时：

每次移除下一步已经不在滑动窗口内的元素。如果要移除的元素不是最大值的元素，那这个值是否移除不会造成太大的影响，移除元素比较麻烦，所以这个元素可以不移除

（2）push 添加元素时：

如果将窗口中新添加的元素添加到队列中，要保证队列依旧单调。新添加的元素是一定要放入队列中的，为了保证队列一直单调，所以要使用 while 循环将后面不符合单调条件的元素全部弹出，然后再将这个值放入

为什么使用单调队列而不是优先级队列，单调队列是自定义的 STL ，因为在对队列进行插入弹出操作时要保证将先进去的那个元素进行弹出

3.6.2 Python 代码实现

1.C++ 代码实现

class Solution {
  private:
  class MyQueue{
    public:
    deque<int> que; // 使用 deque 实现单调队列
    // 出队
    void pop(int value){
      // 如果想将某个值弹出，如果和队列最头上元素相等则弹出
      if(!que.empty()&&value==que.front()) que.pop_front();
    }
    // 入队
    void push(int value){
      // 出队，直到可以将 value 放入合适的位置
      while(!que.empty()&&value>que.back()) que.pop_back();
      // 将该元素入队到合适的位置
      que.push_back(value);	
    }
    // front 方法的重写
    int front(){
      return que.front();
    }
  };
  public:
  vector<int> maxSlidingWindow(vector<int>& nums, int k) {
    MyQueue que;
    vector<int>res;
    for(int i = 0;i<k;i++) que.push(nums[i]); // 先将前 k 个元素按顺序放入队列
    res.push_back(que.front()); // 记录前 k 个元素
    for(int i = k;i<nums.size();i++){ // 遍历后面的元素
      que.pop(nums[i-k]); // 弹出一个元素
      que.push(nums[i]); // 加入这个元素
      res.push_back(que.front()); // 记录当前最大值
    }
    return res;

  }
};

2.Python 代码实现

class Solution:
    class MyQueue: 
        # 1. 定义一个单调队列
        def __init__(self):
            self.queue = list()
        # 2.定义单调队列的入队
        def push(self,x):
            # 不断的将比 x 小的元素出队
            while self.queue and x>self.queue[-1]:
                self.queue.pop()
            self.queue.append(x)
        # 3.定义单调队列的出队
        def pop(self,x):
            # 为了保持单调性，并且没有那么麻烦，只有出队的元素是最大值才将元素出队
            if self.queue and x==self.queue[0]:
                self.queue.pop(0)
        # 4.得到最大值元素
        def front(self):
            return self.queue[0]

    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        dandiao_que = self.MyQueue()
        res = []
        # 1. 先将前 k 个元素全部入栈
        for i in range(k):
            dandiao_que.push(nums[i])
        res.append(dandiao_que.front())
        # 2. 剩余元素
        for i in range(k,len(nums),1):
            # 先将元素出栈
            dandiao_que.pop(nums[i-k])
            # 元素入栈
            dandiao_que.push(nums[i])
            # 得到当前最大值
            res.append(dandiao_que.front())
        return res

3.6.3 时空复杂度

时间复杂度：O(N)

空间复杂度：O(1)

347前 K 个高频元素

LeetCode题目链接

3.7.1 算法描述

(1)整体思路

需要统计每个元素出现的频率，用 Dict / Map 对每个元素进行计数

是用优先级队列（小根堆）对出现的频率进行排序，堆就是一个树

优先级队列类似于一个堆，只能从队头移除元素，从队尾添加元素

这里要是用小根堆对数值进行存储，这里的小跟堆只能存放 k 个元素，所以每次进行弹出时都要将堆中的最小值弹出。因为大根堆最顶部的元素是频率最高的元素，不能将频率高的元素弹出 ，所以要将频率小的值不断的移除

（2）如何构建小根堆：

小根堆本质是优先级队列，priority_map 。在定义它是要定义他的比较规则，比较规则定义如下，就相当于重写 operator 函数

class mycomparion{
  bool operator()(const pair<int,int>& lhs,const pair<int,int>&rhs){
    return lhs.second<rhs.second;
  }
};

构建小根堆时比较规则中保证：

left<right : 从小到大–>小根堆 ； right <left :从大到小–> 大根堆

3.7.2 代码实现

1.C++ 代码实现

class Solution {
  public:
  class mycomparison{
    public:
    bool operator()(const pair<int,int>& lhs,const pair<int,int>& rhs){
      return lhs.second>rhs.second; // 构建小根堆
    }
  };
  public:
  vector<int> topKFrequent(vector<int>& nums, int k) {
    // 使用 map 统计元素出现的频率
    unordered_map<int,int>map; // <nums[i]，出现的次数>
    for(int i =0;i<nums.size();i++) map[nums[i]]++; // 进行计数
    // 小跟堆：对频率进行排序
    priority_queue<pair<int,int>,vector<pair<int,int>>,mycomparison> pri_que;
    // 建立小跟堆
    for(unordered_map<int,int>::iterator it = map.begin();it!=map.end();it++){
      pri_que.push(*it); // 将这个元素添加到小根堆中
      if(pri_que.size()>k){
        pri_que.pop();
      }
    }
    // 遍历堆中元素,从后向前遍历
    vector<int> res(k);
    for(int i=k-1;i>=0;i--){
      res[i] = pri_que.top().first;
      pri_que.pop();
    }
    return res;

  }
};

2.Python 代码实现

class Solution:
    def topKFrequent(self, nums: List[int], k: int) -> List[int]:
        count_dict = Counter(nums) # 对每个数字出现的频率进行记录
        hp = []
        for key,value in count_dict.items():
            if len(hp)<k: # 堆中元素小于 k ，直接添加
                heapq.heappush(hp,(value,key)) # 因为后面要排序，所以将出现频率放在前面
            else: # 弹出堆中最小的元素
                if value>hp[0][0]: # 这一维度就是 tuple 的 value 的值
                    heapq.heappop(hp) # 弹出最小值
                    heapq.heappush(hp,(value,key)) # 插入
        return [x[1] for x in hp]

常见错误：

1.对 heapq 的操作不熟悉，pop 和 push 操作时前面要加 heap

2.最后一步return 时不知道怎么写

3.7.3 时空复杂度

时间复杂度：O(nlogk)

因为堆排序的时间复杂度是 O(nlogn) ，n 是指每次需要遍历 n 个元素，logn 是指树高。但是这里的树高最坏是 logk 所以时间复杂度就是 O(nlogk )

空间复杂度：O(N)

3.7.4 Python 相关库使用

1.Counter 计数器的使用

Counter 返回一个字典，用来计算 list 中每个元素出现的次数

①导包

import collections.Counter

②对数组进行计数，并返回一个字典 dic

dic = Counter(nums)

③遍历字典

for key,value in dic.iterm()

2.堆的函数操作模块

heapq 的介绍

①导包

import heapq

②构建堆

使用一个 list 构建堆

hp = []

③将元素放入堆中

heapq.heappush(堆数组，(元素))

④弹出堆的最小值

heapq.heappop(堆数组)

1.暴力

暴力解法的话需要求 cur 的面积，以及从 cur 到最后一个柱子的最大面积。这里需要用到 短板问题，求 cur 柱子到最后一个柱子的最大面积就是

min(height[cur~n-1])*weight[cur~n-1]

2.使用 DP 的思路

在前两天写了一个同样柱状图的算法，那个题是用 DP 实现的。同样也是 短板问题

但是这一个题和前一个题的不同在于这个题是求实体的面积，也就是柱子的面积，而上次的题是求柱子和柱子之间缝隙的距离。所以在求最大面试时上次的题只需要知道 cur 柱子左侧的做大值和最小值是多少。但是这个题还要知道宽度，cur 到最小高度柱子的宽度是多少。所以这个题用 DP 的话除了记录 minHeight 还要记录 minWeight。

所以这里的短板问题是要求 cur 出左右边界的

3.单调栈

我们需要维持一个单调栈，栈中元素是递增的。每次将一个元素弹出后就要判断面积

这个栈需要保存的元素是每个柱子的 index ,因为保存 index 不仅可以知道它的高度还能求出柱子之间的宽度

155最小栈

算法描述

这里的栈比较特殊，里面传入一个 pair ，第一个 val 用于记录当前 node 的值，另一个元素记录为该 node 以下的所有 node 的最小值
如果是栈的话很容易拿到之前传入的所有结果

cpp 实现

class MinStack {
public:
    stack<pair<int,int>> sta;
    MinStack() {
        
        
    }
    
    void push(int val) {
        if(sta.empty()) sta.push({val,val});
        else sta.push({val,std::min(val,sta.top().second)});
    }
    
    void pop() {
        sta.pop();
    }
    
    int top() {
        return sta.top().first;
    }
    
    int getMin() {
        return sta.top().second;
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(val);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->getMin();
 */