这篇博客介绍了C++实现的多个经典算法题目，包括最大数的加减乘除、汉诺塔、斐波那契数列、帕斯卡三角形、三色旗问题、归并排序、老鼠走迷宫、骑士走棋盘、八皇后问题和八枚硬币问题。通过这些题目，展示了C++在解决算法问题上的应用。
夯实基础，竭力前行！ Xue
目录
文章目录
1,最大数四则运算
输入数numA，numB，输出numOUT，返回位数。>感谢大佬分享，传送门：大数的四则运算（加法、减法、乘法、除法）
1.1加法
int justdoit::bigAdd_16(char *numA, char* numB, int*numOUT)
{
//求出最大长度
int len1 = strlen(numA);
int len2 = strlen(numB);
int len = len1 > len2 ? len1 : len2;
//将char*转换为int*
int arr1[C51_MAXINDEXOFARRAY] = { 0 };
int arr2[C51_MAXINDEXOFARRAY] = { 0 };
for (int idx = len1-1,idx1=0; idx >=0 ; idx--,idx1++) arr1[idx1] = numA[idx] - '0';
for (int idx = len2-1,idx1=0; idx >= 0; idx--,idx1++) arr2[idx1] = numB[idx] - '0';
for (int idx=0; idx <len ;idx++) {
numOUT[idx] = arr1[idx] + arr2[idx];
if(numOUT[idx]>9) {
numOUT[idx] -= 10;
numOUT[idx + 1]++;
}
}
if (numOUT[len] != 0) len++;
return len;}
1.2减法
int justdoit::bigSub_16(char *numA, char *numB, int *numOUT)
{ //求出最大长度
int len1 = strlen(numA);
int len2 = strlen(numB);
int len = len1 > len2 ? len1 : len2;
//转换为整型
int arr1[C51_MAXINDEXOFARRAY] = { 0 };
int arr2[C51_MAXINDEXOFARRAY] = { 0 };
for (int idx = len1 - 1,idx1=0; idx >= 0; idx--,idx1++) arr1[idx1] = numA[idx] - '0';
for (int idx = len2 - 1,idx1=0; idx >= 0; idx--,idx1++) arr2[idx1] = numB[idx] - '0';
//遍历
bool isNegative = false;
if(len1 > len2 ||(len1 == len2 && numA[len1-1] >= numB[len2-1]))
for (int idx = 0; idx < len; idx++) {
numOUT[idx] = arr1[idx] - arr2[idx];
if (numOUT[idx] < 0) {
numOUT[idx] += 10;
numOUT[idx+1] -=1; }
} else {
for (int idx = 0; idx < len; idx++)
{ numOUT[idx] = arr2[idx] - arr1[idx];
if (numOUT[idx] < 0) { numOUT[idx] += 10;
numOUT[idx+1] -=1; }
}
isNegative = true;
}
for(int idx=len -1;idx >=0;idx--)
{
if(numOUT[idx] >0)
{
len= idx+1;
if(isNegative)
numOUT[idx]=-1;
}
}
return len;
}
1.3乘法
int justdoit::bigMul_16(char *numA, char *numB,int *numOUT){
//归置
for (int idx = 0; idx < C51_MAXINDEXOFARRAY; idx++)
numOUT[idx] = 0;
//求出最大长度
int len1 = strlen(numA);
int len2 = strlen(numB);
int len = 0;
//转换为整型
int arr1[C51_MAXINDEXOFARRAY] = { 0 };
int arr2[C51_MAXINDEXOFARRAY] = { 0 };
for (int idx = len1 - 1, idx1 = 0; idx >= 0; idx--, idx1++) arr1[idx1] = numA[idx] - '0';
for (int idx = len2 - 1, idx1 = 0; idx >= 0; idx--, idx1++) arr2[idx1] = numB[idx] - '0';
//遍历
int carryNum = 0;
for (int idx=0;idx < len1;idx++)
{
for (int idx1=0;idx1 <len2;idx1++)
{
len = len < (idx + idx1) ? (idx1 + idx) : len;
numOUT[idx+idx1] += arr1[idx] * arr2[idx1] + carryNum;
if (numOUT[idx+idx1] > 9)
{
carryNum = numOUT[idx+idx1] / 10;
numOUT[idx+idx1] = numOUT[idx+idx1] % 10;
} else
carryNum = 0;
if (carryNum != 0 && idx1== len2-1)
len++;
}
}
return len;}
1.4除法
//除法(不计算小数点)
int justdoit::bigDiv_16(char *numA, char *numB,int *numOUT){
//归1é置?
for (int idx = 0; idx < C51_MAXINDEXOFARRAY; idx++)
numOUT[idx] = 0;
//求ó出3?最×?大′ó长3¤度è
int len1 = strlen(numA);
int len2 = strlen(numB);
int len = 0;
//转×a换?为a整?型Dí
int arr1[C51_MAXINDEXOFARRAY] = { 0 };
int arr2[C51_MAXINDEXOFARRAY] = { 0 };
for (int idx = len1 - 1, idx1 = 0; idx >= 0; idx--, idx1++)
arr1[idx1] = numA[idx] - '0';
for (int idx = len2 - 1, idx1 = 0; idx >= 0; idx--, idx1++)
arr2[idx1] = numB[idx] - '0';
if(len1 < len2) return 1;
char cTmp[C51_MAXINDEXOFARRAY];
int resultTmp[C51_MAXINDEXOFARRAY] ={0};
strcpy(cTmp,numA);
int maxLen =0;
do {
int len = justdoit::bigSub_16(cTmp,numB,resultTmp);
if(resultTmp[len] <0) break;
for(int idx=0;idx < len1; idx++)
{
if(idx < len)
cTmp[len1-1-idx] = resultTmp[idx]+'0'; else cTmp[len1-1-idx] ='\0';
}
memset(resultTmp,0,C51_MAXINDEXOFARRAY);
numOUT[0]++;
//进?位?检ì查2é
if(numOUT[0] >9)
{
for(int idx=0;idx< C51_MAXINDEXOFARRAY-1;idx++){
if(numOUT[idx] >9)
{
numOUT[idx] = numOUT[idx]%9;
numOUT[idx+1] +=1;
}
if(numOUT[idx+1] <9)
break;
}
}
}while(1);
return 0;}
2汉诺塔(河内之塔Towers of Hanoi)
感谢大佬分享，传送门：精典算法之详解 河内之塔
如图所示，从1柱转到3柱，转移过程保持大盘子始终在下面。
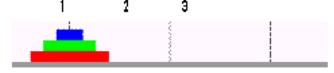
这里将问题分解为2块移动，如果2个以上的其下当作一体，有下面这幅图看到2个时的移动步骤
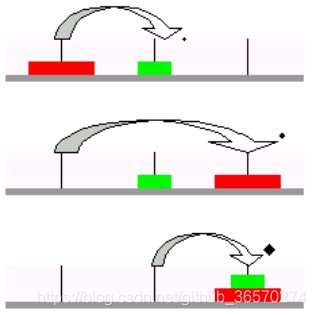
void justdoit::hanoi_1(int n,char A,char B,char C)
{
if(n==1)
{
cout<<"Move "<<n<<" from "<<A<<" to "<< C <<endl;
}
else
{
hanoi(n-1,A,C,B); //把A柱子上第N-1个盘子通过C放到B柱子上
cout<<"Move "<< n<<" from "<< A <<" to "<< C <<endl;
hanoi(n-1,B,A,C); //把B上所有盘子通过A放到C上
}
}
3,费列数列
当前数列值=前两数列值之和，如0，1，1，2，3，5，8。。。
int justdoit::fibCpp_2(int n)
{
if(0==n)
return 0;
if(1==n)
return 1;
return fibCpp_2(n-1)+fibCpp_2(n-2);
}
4,巴斯卡三角形(杨辉三角)
1、每行数字左右对称，由1开始逐渐变大，然后变小，回到1。
2、第n行的数字个数为n个。
3、第n行数字和为2^(n－1)。
4、每个数字等于上一行的左右两个数字之和。可用此性质写出整个帕斯卡三角形。
5、将第2n+1行第1个数，跟第2n+2行第3个数、第2n+3行第5个数……连成一线，这些数的和是第2n个斐波那契数。将第2n行第2个数，跟第2n+1行第4个数、第2n+2行第6个数……这些数之和是第2n-1个斐波那契数。
6、第n行的第1个数为1，第二个数为1×(n-1)，第三个数为1×(n-1)×（n-2）/2，第四个数为1×(n-1)×（n-2）/2×（n-3）/3…依此类推。
针对该三角形有两种求解方式，一种是公式法，另一种是推导法。p = p * (n-i+1) / i
#define PASCARRLEN 5
//注：此代码由推理而来，公式法套用即可，公式由来没太搞明白，搞明白公式再做补充说明
void justdoit::pscaTri_3(int n)
{
int a[PASCARRLEN][PASCARRLEN], i , j ;
for(i=0;i<PASCARRLEN;i++)
for(j=0;j<=i;j++)
{
if(i==j||j==0) //每行开始和结束为止都为1
a[i][j]=1;
else
a[i][j]=a[i-1][j]+a[i-1][j-1]; //其他部分由上一行相邻两数求和
cout<< a[i][j];
if(i==j)
cout<<endl;
}
return ;
}
5,三色旗
一组字符数组中只有’b’,‘w’,‘r’，将其按照b···bw····wr····r循序依次排列，要求步骤数最少。
设置三个指针
wFlag：移动指标
bFlag：第一个非b指标
rFlag：最后一个非r指标
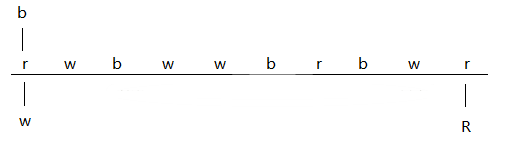
void swap(int x,int y,char *color)
{
char temp;
temp = color[x];
color[x] = color[y];
color[y] = temp;
}
void justdoit::_3ColorFlag_4(void)
{
char color[] = {'r','w','b','w','w','b','r','b','w','r','\0'};
int wFlag = 0;//移动指标
int bFlag = 0;//第一个非b指标
int rFlag = strlen(color)-1;//最后一个不是r指标
int i;
while(wFlag <= rFlag)
{
if(color[wFlag] == 'w')//移动指标遇到的为w,则进位
{wFlag++;}
else if(color[wFlag] == 'b')//如果为b，替换b和w，替换后第一个非b指标前进一位，移动指标前进一位
{
swap(bFlag,wFlag,color);
bFlag++;wFlag++;
}else{ //如果为r，保证移动指标始终小于最后一个r指标
while(wFlag < rFlag && color[rFlag] == 'r')//遍历找到最后一个非r指标
rFlag--;
swap(rFlag,wFlag,color);//将rFlag指标转为r指标
rFlag--;//退位为非r指标
}
}
for (i = 0 ; i < strlen(color) ; i++)
cout << color[i];
cout <<endl;
}
6, 归并排序(分治法)
分治法的一个应用，详细解释传送门:归并排序详解
int num[10] = { 2,3,1,5,7,6,8,0,9,4 }; //待排序数组
int temp[10]; //备用数组
using std::cout;
void MergeSort(int *num, int start, int end);
void Merge(int * num, int start, int mid, int end);
void MergeSort(int * num, int start, int end)
{
int mid = (start + end) / 2;
if (start < end)
{
MergeSort(num, start, mid);
MergeSort(num, mid + 1, end);
Merge(num, start, mid, end);
}
}
void Merge(int * num, int start, int mid, int end)
{
int i, j, k;
i = start;
j = mid + 1;
//这里采用了双指针法，将一个段落分为两部分进行排序
for (k = start; i <= mid && j <= end; k++)
{
if (num[i] <= num[j])
{
temp[k] = num[i++];
}
else
{
temp[k] = num[j++];
}
}
//这里补全，这里的mid前后两部分是按照顺序排列的
while (i <= mid)
{
temp[k++] = num[i++];
}
while (j <= end)
{
temp[k++] = num[j++];
}
for (int i = start; i <= end; i++) //将temp中的数据拷贝回num中
{
num[i] = temp[i];
}
}
int main()
{
MergeSort(num, 0, 9);
for (int i = 0; i < 10; i++)
cout << num[i] << std::endl;
system("pause");
}
7，老鼠走迷宫(回溯法)
给定一个二维数组，数组中2表示墙壁，0表示通路，由此数组可展示为一个迷宫图。给定入口位置和出口位置，判断之间是否存在通路并显示出走出迷宫的道路。
**解题思路：**从开始点开始，分别从四个方向开始遍历，
//给定部分
int visit(int , int );
int maze[7][7] = {
{2, 2, 2, 2, 2, 2, 2},
{2, 0, 0, 0, 0, 0, 2},
{2, 0, 2, 0, 2, 0, 2},
{2, 0, 0, 2, 0, 2, 2},
{2, 2, 0, 2, 0, 2, 2},
{2, 0, 0, 0, 0, 0, 2},
{2, 2, 2, 2, 2, 2, 2}
};//迷宫，其中2为墙壁，0为通道
int startI = 1, startJ = 1;//入口
int endI = 5, endJ = 5;//出口
int success = 0;//是否成功
int visit(int i, int j)
{
maze[i][j] = 1;//标记走过的位置为1
if(i == endI && j == endJ)//检测是否到了出口
success = 1;
//如果没在出口，则在四个方向进行试探
if(success != 1 && maze[i][j+1] == 0)
visit(i, j+1);
if(success != 1 && maze[i+1][j] == 0)
visit(i+1, j);
if(success != 1 && maze[i][j-1] == 0)
visit(i, j-1);
if(success != 1 && maze[i-1][j] == 0)
visit(i-1, j);
//1,每一次函数调用后都会有一次返回，当程序流执行到某一级递归的结尾处，它会转移到前一级递归继续执行
//2，位于递归调用语句前的语句的执行顺序和各个被调用函数的顺序相同，位于递归调用语句后的语句的执行顺序和各个被调用函数的顺序相反。
//如果求所有路径，将递归中成功的标志去掉，即允许在找到出口的情况下，做多余步骤。在条件i == endI && j == endJ时绘制出所有的路径即可
if(success != 1)
maze[i][j] = 0;
return success;
}
8,骑士走棋盘(动态规划法)
J.C.Warnsdorft提出：先将最难的位置走完，接下来的路就宽广了
理论上每一个点，可以走八个方向，统计八个方向可走的，在可走的前提下，统计每一个的下一步可走的个数，个数最少的认为时"正确"的下一步。
是一个多阶段决策优化问题，属于动态规划法范畴
int travel(int x, int y);
int board[8][8] = {0}; //代表整个棋盘
int travel(int x, int y)
{
int ktmove1[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int ktmove2[8] = {1, 2, 2, 1, -1, -2, -2, -1};
//对应了骑士能走的八个方向
int nexti[8] = {0}; //这两行存储的是可走的下一步的坐标
int nextj[8] = {0}; //
int exists[8] = {0}; //记录每个可走下一步的可走下一步个数
int i, j, k, m, l;
int tmpi, tmpj;
int count, min, tmp;
i = x; j = y;
board[i][j] = 1; //将起点坐标置为1
for(m = 2; m <= 64; m++)//通过循环来标记2-64
{
for(l = 0; l < 8; l++)
exists[l] = 0; //这个数组是每次循环都要重复利用的，所以重置0
l = 0; //这个l也是重复利用的
//统计8个方向的可行性个数，及相应的位置坐标
for(k = 0; k < 8; k++)
{
tmpi = i + ktmove1[k];
tmpj = j + ktmove2[k];
if(tmpi < 0 || tmpj < 0 || tmpi > 7 || tmpj > 7) //通过此来筛选是否可走
continue;
if(board[tmpi][tmpj] == 0)//如果可走，就将可走的坐标存储在nexti，nextj中
{
nexti[l] = tmpi;
nextj[l] = tmpj;
l++; //把下一步可走位置加一
}
}
//初始坐标下的可走方向个数
count = l;
if(count == 0)//没有下一步可走，就返回
{
return 0;
}
else if(count == 1)//只有一个位置可走，就选择这一步，然后继续循环
{
min = 0;
}
else //有多个位置可走时，判断哪一个可走位置的下一步的可走位置最少，就走这一步，意思是把
{ //把最困难的走了，这样接下来的空间就大了，可以走完所有位置的可能性就变大了
for(l = 0; l < count; l++) //同时也说明这种非递归的方法不一定对于所有初始位置都能
{ //走遍全图，因为毕竟这种算法使用概率的原理
for(k = 0; k < 8; k++)
{
tmpi = nexti[l] + ktmove1[k];
tmpj = nextj[l] + ktmove2[k];
if(tmpi < 0 || tmpj < 0 || tmpi > 7 || tmpj > 7)
{
continue;
}
if(board[tmpi][tmpj] == 0)
exists[l]++; //记录可走位置下一步可走位置的个数
}
}
tmp = exists[0];
min = 0;
for(l = 1; l < count; l++)
{
if(exists[l] < tmp) //取得可走位置下一步可走位置最少的那个坐标
{
tmp = exists[l];
min = l;
}
}
}
i = nexti[min];
j = nextj[min];
board[i][j] = m; //将当前步数赋值给那个可走位置下一步可走位置最少的那个坐标
}
return 1;
}
9，八皇后(回溯法)
在西洋棋中，皇后只能直线/斜直线走，可以吃掉任何的棋子。即每个棋子在其横竖方向只有它一个。
//9,八皇后
int arry_9[8][8]={0};
int map_9=0;
void print(){//打印结果
cout <<"方案"<<map_9<<":"<<endl;
for(int i=0;i<8;i++){
for(int m=0;m<8;m++){
if(arry_9[i][m]==1){
cout<<"o";
}
else{
cout<<"+";
}
}
cout<<endl;
}
cout<<endl;
}
bool check(int k,int j){//判断节点是否合适
for(int i=0;i<8;i++){//检查列冲突，此前的迭代是基于每行的，因此每行肯定只有一个
if(arry_9[i][j]==1){
return false;
}
}
for(int i=k-1,m=j-1; i>=0 && m>=0; i--,m--){//检查左对角线(左上部分，右下不需要，因为没遍历到)
if(arry_9[i][m]==1){
return false;
}
}
for(int i=k-1,m=j+1; i>=0 && m<=7; i--,m++){//检查右对角线(右上部分，左下不需要，没遍历到)
if(arry_9[i][m]==1){
return false;
}
}
return true;
}
void justdoit::findDif8Queen(int i)
{
if(i>7){//遍历完行，即意味着有解
map_9++;//统计解个数
print();//打印八皇后的解
return;
}
for(int m=0;m<8;m++){//深度回溯,递归算法，遍历检测列
if(check(i,m)){//检查皇后摆放是否合适，当列合适的时候，进入循环体，标记然后，行数加1进入下一行，记得归零，单次遍历完回溯到递归的下一步，此时归零。
arry_9[i][m]=1;
findDif8Queen(i+1);
arry_9[i][m]=0;//清零，以免回溯的时候出现脏数据
}
}
}
10，八枚硬币
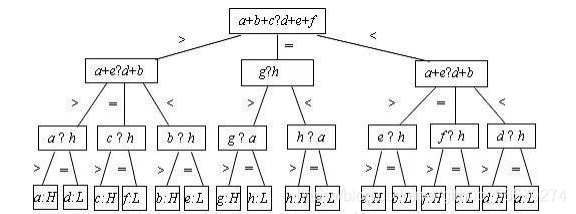
八枚外观相同的硬币中，有一枚是假币，并且已知假币和真币的重量不同，但不知道假币和真币相比较轻还是较重。可以通过一架天平来任意比较两组硬币，设计高效算法
将整体上分为三部分，分析三部分之间的关系，具体的逻辑如下图所示，感谢分享，传送门:算法设计与分析之八枚硬币问题
//10，八硬币
//显示
//fake假币，real真币，判断同真币的大小关系，i为假币的索引位置
void print_10(int fake, int real, int i)
{
if(fake > real)
{
cout<<"位置在："<<(i + 1)<<"是假币!"<<"且偏重!";
}
else {
cout<<"位置在："<<(i + 1)<<"是假币!"<<"且偏轻!";
}
}
//a,b中含有假币，real真币，idex1，idex2分别为a,b的索引
void compare_10(int a, int b,int real, int index1,int index2)
{
if(a == real)
{
print_10(b,real,index2);
}
else
{
print_10(a,real,index1);
}
}
void justdoit::eightcoin(int arr[])
{
int abc = arr[0] + arr[1] + arr[2];
int def = arr[3] + arr[4] + arr[5];
int a = arr[0];
int b = arr[1];
int c = arr[2];
int d = arr[3];
int e = arr[4];
int f = arr[5];
int g = arr[6];
int h = arr[7];
if(abc > def)// gh为真币
{
if((a+e)>(d+b))//假币在a,d中
compare_10(a,d,g,0,3);
else if((a+e)==(d+b))//假币在c,f中
compare_10(c,f,g,2,5);
else //假币在b,e中
compare_10(b,e,g,1,4);
}
else if(abc == def)// gh中有假币
{
if(a != g)//g为假币
compare_10(a,g,a,0,6);
else//h为假币
compare_10(a,h,a,0,7);
}
else // gh为真币
{
if((a+e)>(d+b))//假币在b,e中
compare_10(b,e,g,1,4);
else if((a+e)==(d+b))//假币在c,f中
compare_10(c,f,g,2,5);
else //假币在a,d中
compare_10(a,d,g,0,3);
}
}
扫一扫
483
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
