代码随想录算法训练营第三天|203.移除链表元素、707.设计链表、206.反转链表

最新推荐文章于 2025-12-31 21:25:26 发布

原创最新推荐文章于 2025-12-31 21:25:26 发布 · 939 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #链表 #数据结构

链表基础

链表也是描述线性表的一种方式，相比数组元素在计算机连续的空间中存储，链表的元素在内存中的存储为随机的，因此，需要有一个明确的指针（链）来指示下一个元素的位置（地址），即最简单的链表元素有值val和下一个元素的地址指针*next构成，在此之上，可以加入前一个元素的地址指针*prev构成双向链表，在链表最后一个元素的指针指向该链表的头结点可构成循环链表等。为了方便起见，之后的链表元素统称为结点。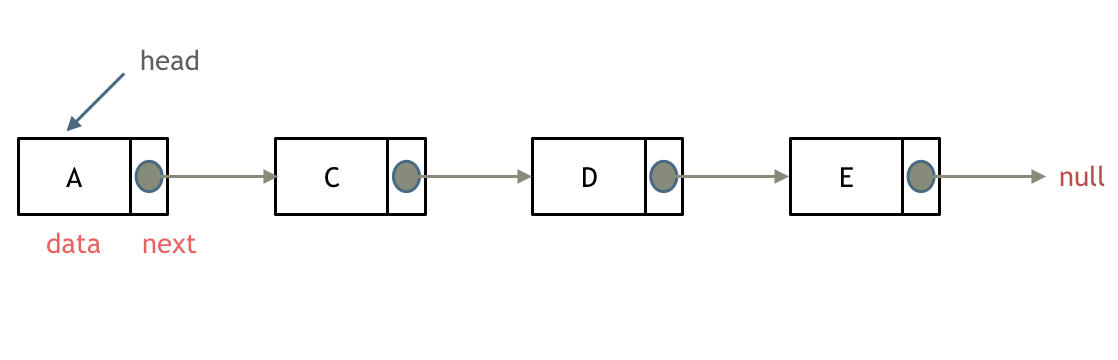

单向链表

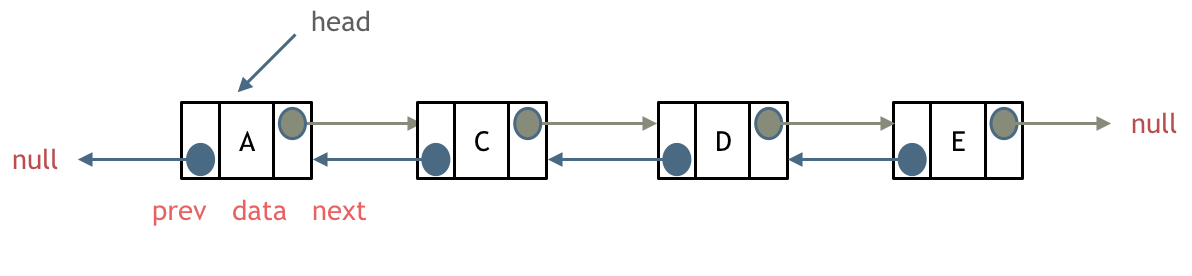
双向链表

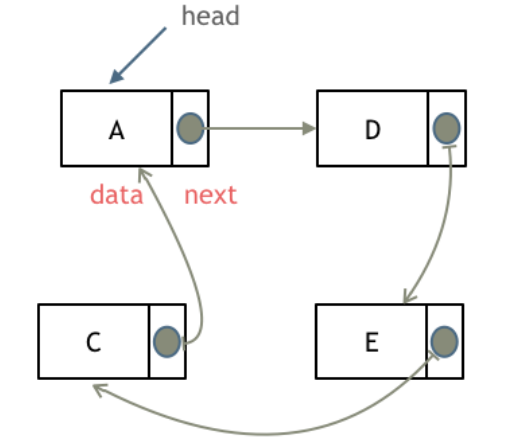
循环链表

也正是因为随机的存储方式，相比数组，对链表中数据的搜寻通常需要遍历整个链表，算法时间复杂度为O(n)，而对链表中数据的增删操作则只需要O(1)的时间复杂度，具体的增删操作在后题详述。

在C++的STL中，容器类list是使用带头节点的双向循环，同样有erase和insert函数用于删除数据和添加数据。

链表的定义

以C++为例，若使用结构定义，需一个val和指向下一个结点的指针*next，若不存在下一个结点，*next指向NULL或nullptr（c++）。

struct ListNode{
    //数据成员
    int val;//该结点上的值
    ListNode *next;//指向下一个结点的指针
    //方法
    ListNode(int x): val(x), next(NULL){}//结点的构造函数
};

链表的增删

增加结点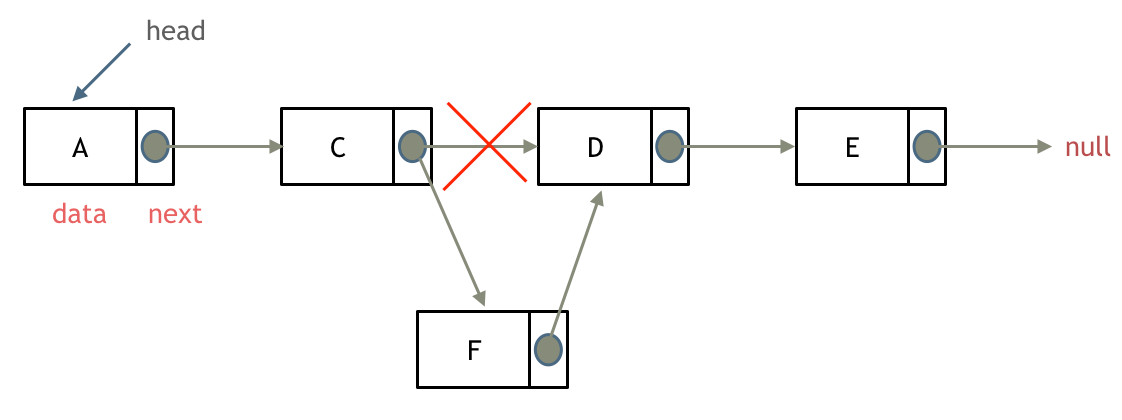

这里的增加结点可以和数组中增加元素进行对比，在数组中，找到第i个位置，将所有后续位置的元素后移，将该位置覆盖为你想要增加的值；在链表里，我们同样需要先找到这样一个位置，但相比数组，我们找到需要增加结点的位置的前一个位置结点rear，记录下rear指向的下一个结点的位置(rear->next)，设增加的结点为temp，将temp的next指针指向原结点temp->next = rear->next，之后将rear的next指针指向temp，即完成了链表元素的插入，需要注意这个顺序，否则会出错。

删除结点

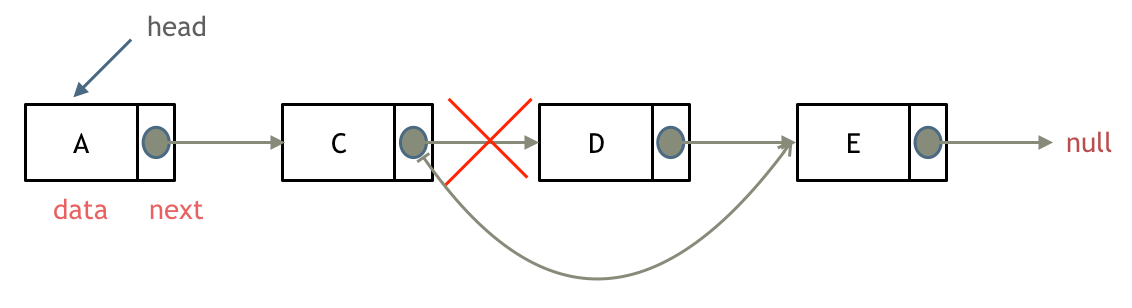
对链表的删除操作同样可以与数组进行对比，数组删除i位置的结点需要找到位置i，将所有后续元素前移进行覆盖，在链表中，我们找到需要删除结点的位置的前一个位置结点rear，记录下rear指向的下一个结点的下一个结点的位置(rear->next->next)，由于C++中需要对删除结点的内存进行回收，防止内存泄漏，我们需要创建一个temp，将temp等同于需要删除的结点，temp = rear->next,将rear->next = rear->next->next，即完成了链上元素新的连接，最后delete temp，完成对内存的回收，真正地完成删除结点的删除操作。这个操作顺序同样非常重要。增删操作的算法时间复杂度都为O(1)，但查找元素的复杂度为O(n)。

203.移除链表元素

基本思路和前文对链表元素的删除相似，但需要注意的是，由于需要返回的是头结点head，若需要删除的元素在头部（将head变为head->next，并删除原head）和在其他位置（如上文所述）存在步骤上的区别，此处考虑加入一个虚拟头结点dummy，虚拟头结点dummy->next即为需要返回的head。算法遍历链表的时间复杂度为O(n)，删除操作的时间复杂度为O(1),空间复杂度为O(1)。

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        if(!head){
            return nullptr;
        }//当head为空时直接返回空指针
        ListNode * dummy = new ListNode(0); //创建一个哑元变量，虚拟头结点，其next用于指向head，方便删除操作的统一
        dummy->next = head;
        ListNode * cur = dummy;//创建位置指示cur，用于指向当前遍历链表的位置
        
        while(cur->next){//此处while循环中条件为cur->next非空，即存在下一个链表结点
            if(cur->next->val == val){//当当前结点的下一个结点的val值为需要删除的值时，进行删除，与前文对删除的描述相同
                ListNode* to_delete = cur->next;
                cur->next = cur->next->next;
                delete to_delete;//释放空间
            }
            else{
                cur = cur->next;//如果不满足条件，向后逐步遍历
            }

        }
        return dummy->next;//由于需要返回的是头结点head，返回dummy->next;
    }
};

注意此处cur指向的是dummy，即虚拟头结点。

707.设计链表

class MyLinkedList {
private:
    struct ListNode{
        int val;
        ListNode*next;

        ListNode():val(0),next(nullptr){};
        ListNode(int x):val(x),next(nullptr){};
    };//定义链表结构
    int len;//增加一个长度用于判断增删的特殊情况
    ListNode* dummy;//增加虚拟头结点

public:
    MyLinkedList() {
        len = 0;
        dummy = new ListNode();//初始化，长度为0，仅有一个虚拟头结点
    }

    int get(int index) {//此处写的较麻烦，本来不想用len，后面加入len，这里可大改
        if(!dummy->next){
            return -1;
        }//当链表为空时，返回-1
        int count = index;
        ListNode*cur = dummy->next;
        while(count!=0){
            if(cur->next){
                cur = cur->next;
                count--;
            }
            else
                return -1;
        }//循环index次，若在能完整循环完，则能找到，否则返回-1
        return cur->val;
    }

    void addAtHead(int val) {//在虚拟头结dummy后添加结点
        ListNode* head = new ListNode();
        head->val = val;
        head->next = dummy->next;
        dummy->next = head;
        len++;//添加完成后，长度len++
    }

    void addAtTail(int val) {//添加尾结点
        if(!dummy->next){//若长度为空，等同于添加头结点
            addAtHead(val);
        }
        else{//否则，遍历到尾部，新增结点，长度len++
            ListNode*tail = new ListNode();
            tail->val = val;
            tail->next = nullptr;
            ListNode*cur = dummy->next;
            while(cur->next){
                cur = cur->next;
            }
            cur->next = tail;
            len++;
        }
        
    }

    void addAtIndex(int index, int val) {//这里需要注意index若大于len或小于0都应return，否则                    
                                        //会无法通过
        if(index==len) addAtTail(val);
        else if(index<0||index>len) return;
        else{//利用for循环找到index前的结点，并完成添加操作
            ListNode* cur =dummy;
            for(int i=0;i<=index-1;i++){
                cur = cur->next;
            }
            ListNode* newnode = new ListNode();
            newnode->val = val;
            newnode->next = cur->next;
            cur->next = newnode;
            len++;
        }

    }

    void deleteAtIndex(int index) {//利用get函数，判断链表index的元素是否存在，存在才进行操作
        if(get(index)==-1) return;
        ListNode* cur = dummy;
        for(int i=0;i<=index-1;i++){
            cur = cur->next;
        }//同样利用for寻找index前结点，并完成删除之后结点的操作
        ListNode* temp = cur->next;
        cur->next = temp->next;
        delete temp;//删除temp，释放空间
        len--;
    }
};

对我来说值得注意的几个点

1.addAtIndex，若Index超出结尾也需要直接return，而不是加到末尾，如果加到末尾的话，leetcode会无法通过。

2.长度len的加入，方便了对特殊情况的判断。

3.若index在len长度内，add和delete操作要寻找链表index前的元素，可用以下for循环实现

for(int i=0;i<=index-1;i++){
    cur = cur->next;
    }

while循环也能实现，但我不太熟悉，需要再多写写。

4.虚拟头结点的加入极大地方便了在链表中增删，统一了链表中所有位置增删的方式。

206.反转链表

一.直观思路

将链表中所有元素存入一个数组中，后对数组中元素进行反向遍历，依次加入到新的链表中，并返回头指针。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(!head){
            return nullptr;
        }
        else{
            vector<int>nums{};
            ListNode *cur = head;
            while(cur->next){
                nums.push_back(cur->val);
                cur = cur->next;
            }
            nums.push_back(cur->val);
            ListNode *dummy = new ListNode();
            ListNode *cur1 = dummy;
            int nums_cur = nums.size() - 1;
            while(nums_cur>= 0){
                ListNode *newadd = new ListNode(nums[nums_cur--]);
                cur1->next = newadd;
                cur1 = cur1->next;
            }
            return dummy->next;
        }
    }
};

算法时间复杂度O(n)，空间复杂度O(n)

二.双指针法

创建两个指针pre和cur，都指向头结点，pre用于保存反转后cur指针指向的地址。实际在循环中有第三个指针temp用于记录cur后的结点地址，但只用循环遍历链表一次，算法的时间复杂度还是O(n)，或许这才是双指针的意思？不过我看leetcode上称这为迭代方法，不过也不重要了，记住思想。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(!head){
            return nullptr;
        }
        else{
            ListNode*cur = head;
            ListNode*pre = nullptr;//反转第一个结点应指向nullptr
            while(cur->next){
                ListNode*temp = pre;//先保存反转后结点指向的位置
                pre = cur->next;//令pre指向cur->next,防止之后赋值后链表断裂
                cur->next = temp;//将cur指向反转后的位置
                temp = pre;//改变temp保存下一个指针的位置
                pre = cur;//pre保存下一个指针反转后的位置
                cur = temp;//cur变为正序的下一个指针
            }
            cur->next = pre;
            return cur;
        }
    }
};

卡哥视频里while中选择cur而不是cur->next，且更好理解，周末有时间再更新一下。如下

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* temp; // 保存cur的下一个节点
        ListNode* cur = head;
        ListNode* pre = NULL;
        while(cur) {
            temp = cur->next;  // 保存一下 cur的下一个节点，因为接下来要改变cur->next
            cur->next = pre; // 翻转操作
            // 更新pre 和 cur指针
            pre = cur;
            cur = temp;
        }
        return pre;
    }
};

算法空间复杂度O(1)，时间复杂度由于同样需要遍历O(n)。

三.递归算法

不太理解，周末需再看看。

class Solution {
public:
    ListNode* reverse(ListNode* pre,ListNode* cur){
        if(cur == NULL) return pre;
        ListNode* temp = cur->next;
        cur->next = pre;
        // 可以和双指针法的代码进行对比，如下递归的写法，其实就是做了这两步
        // pre = cur;
        // cur = temp;
        return reverse(cur,temp);
    }
    ListNode* reverseList(ListNode* head) {
        // 和双指针法初始化是一样的逻辑
        // ListNode* cur = head;
        // ListNode* pre = NULL;
        return reverse(NULL, head);
    }

};

时间复杂度仍为O(n),但空间复杂度由于递归O(n)，这么想的话，这里纯粹只是炫技的作用，哈哈