基于决策树的OSN连通性模型

基于网络连通性的改进机会传感器 网络连通性监测模型

1 引言

机会传感器网络（OSNs）是一类自组织网络，其中节点可以通过移动进行相互 通信，不需要源节点与目标节点之间保持稳定的链路[1]。具有低成本和短距离 通信能力的智能设备可使无线传感器网络实现巨大改进，并几乎为各个行业创 造新的机遇，例如通信科学[2],能耗[3],数据收集[4]以及信息攻击[5]。然而， 在OSNs中难以维持稳定的拓扑结构，且由于通信范围较大，预测网络拓扑也较 为困难
本文由国家自然科学基金（61762065，61363015）和江西省自然科学基金（20171ACB20018， 20171BBH80022）资助。
©施普林格·自然新加坡私人有限公司 2019 S. Shen 等 (编): CWSN 2018, CCIS 984, 第 64–76 页,
2019.https://doi.org/10.1007/978-981-13-6834-9_7
本文档由 funstory.ai 的开源 PDF 翻译库 BabelDOC v0.5.10 (http://yadt.io) 翻译，本仓库正在积极的建设当中，欢迎 star 和关注。
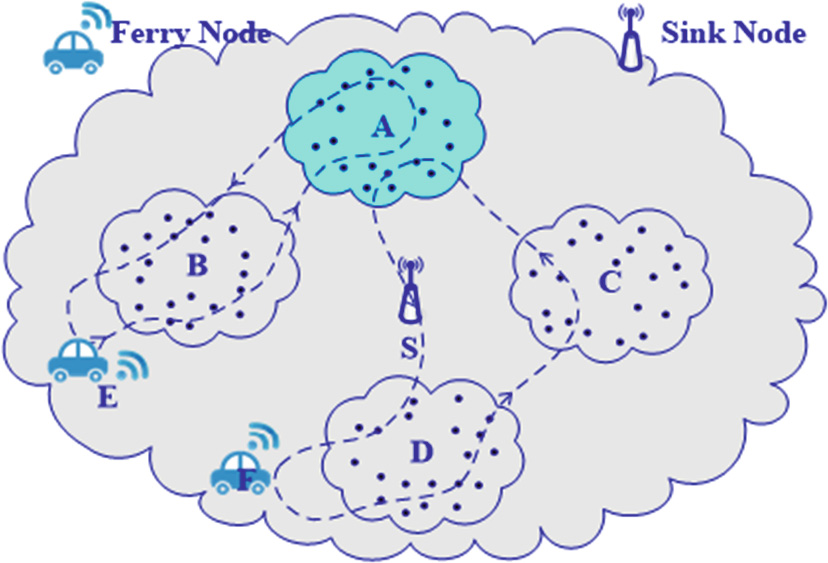
节点频繁移动。此外，整个网络可能已被划分为不同的部分，称为孤岛，这意 味着它们无法直接交换数据，如图 1所示。因此，节点的通信范围受限，需要 渡船[6]节点在孤岛之间传输数据。
节点的移动导致连通性具有机会性、不连续性和动态性。通过节点的相遇 机会以及相关消息传递策略，可以提高数据质量。为了研究机会传感器网络的 连通性，需要研究节点的移动模式，包括节点的位置和方向。作为网络性能的 关键参数，机会传感器网络的连通性与传统网络有显著不同。因此，构建连通 性监测模型以评估网络连通性，对于网络设计和监控而言是必要且重要的。

2 相关工作

在传统传感器网络中，传感器是统计部署的，且拓扑结构不频繁变化。[5]中 的描述将此类网络表示为静态图，其连通性模型可用3‐连通图表示，表明该图 中每个顶点都能找到一条连接到另一顶点的边，且它们之间的距离小于传输范 围。在无线传感器网络（WSNs）中，通过依赖传感器设备的能量消耗方法来 延长网络的生命周期。Patil 等人[7]提出了一种通过降低传感器设备能量消耗 来改善网络连通性的思路。为了克服因簇头选择导致的能量效率低下而引发的 连通性丢失问题，他们提出了一种PS‐LEACH算法，该算法通过计算节点连通 性来选择簇头。通过该算法，可将网络寿命提高88.73%以上，网络连通性提升 约34.3%。在[8]中提出了一种方法，用于模拟网络连通性及隐终端效应对网 络拓扑的影响，基于如下假设：

一种改进的机遇式传感器网络连接性监测模型 65

当n表示网络规模，r表示传输范围，l表示二维方形监控区域的边长时，网络连 通性可以被优化，因此我们有关系式n r2 ¼ l2 log2l。文献[9]中提出了一种 基于邻居辅助的连通性恢复协议（NACRP）。NACRP自动选择一部分传感器 节点作为缺乏连通性的节点的中继节点。该协议依赖于一组中继节点和必要的 发射功率来恢复网络连通性。
但在动态网络中，拓扑结构一直在变化，因此很难将此类网络建模为静态 图。赵等人[10]对网络拓扑进行快照，并利用网络的平均节点度来改善移动网 络中的网络连通性。通过曲线拟合分析获得节点传输半径和网络连通性，可用 于部署节点。盛等人在[11]中研究了在任意凸区域内RWP移动模式下的移动自 组织网络（MANETs）的连通性。MANETs具有一定的传输范围和k‐连通网络， 能够在MANETs中实现高容错性。郭等人[12]研究了存在无线信道衰落时 MANETs的三个基本特征（节点度分布、平均节点度和最大节点度）。这些结 果对于研究激励协议的连通性和算法复杂度非常有用。MANETs中连通性研究 的前提是确保完整的端到端路径，这使得网络的连通性和节点度在机会传感器 网络中不适用。
对于机会传感器网络，王宇等人[13]提出了一种针对车载自组织网络的连 通性分析模型。该模型根据出入口的位置分布考虑了不同情况。为了计算连通 概率，模型考虑了车辆到达率、车辆速度以及车辆节点通过出入口的概率。此 外，[14]中的工作基于n个车辆按照泊松过程随机到达的假设，预测车对车网 络的连通性。车载自组织网络具有通用自组织网络的分布式、无中心、多跳组 网、动态拓扑等特征。机会传感器网络可应用于间歇性连通、大延迟和高误码 率等场景。本文采用合适的连通性监测模型对机会传感器网络中的网络连通性 进行分析。

3 连通性建模

3.1 连通性参数定义

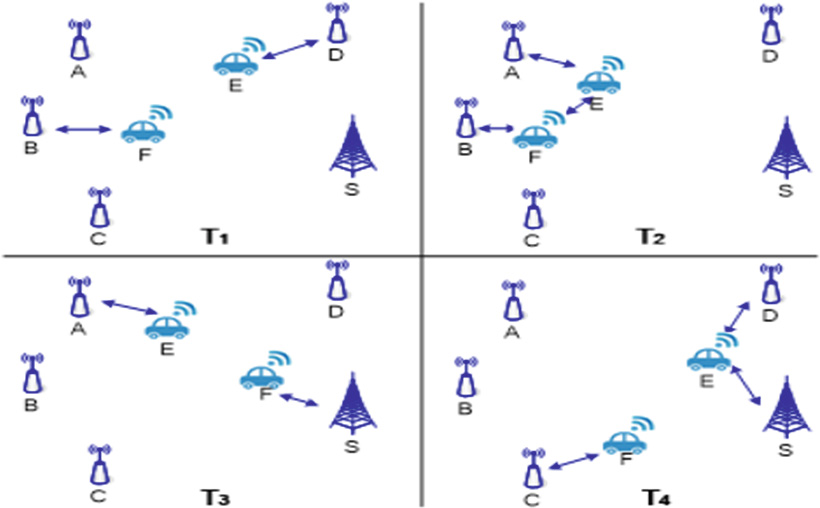
在本章中，我们介绍了一些用于描述网络连通性的参数，其中部分参数已在我 们先前的工作中给出[15]。为了动态地研究机会传感器网络的连通性，我们使 用时间片来记录网络拓扑的状态。以图1中的网络为例，我们采用四个有序的 时间片，即T1、T2、T3、T4，并对每个时间片进行快照。这些快照的结果如 图2所示。
在图2中，A、B、C和D是发送消息的区域，我们称它们为区域节点。E、 F是传输消息的渡船节点。S是处理消息并获取快照的汇聚节点。

定义1：演化图h

给定一个图 G =(V,E)，其中 V 是节点，E 是边。给定其子图的一个有序序列 SG ¼ G1; G2; . . .; GT，其中 UT i¼1Gi ¼ G。给定 ST ¼ t0; t1; t2; . . .; tT是时间实例的有序序 列，且 Gi是 ðti1; tiÞ的子图。最后，我们将 h ¼ ðG; ST ¼; STÞ定义为一个演化图。

定义2：连通路径CJ

给定一组不重复的顶点 VT ¼V1; V2; V3; . . .VT，令 Vt¼1;2;3;4;…;T ¼ h。则 h 表示演化 图。于是，对应的一组时间片 ST ¼t1; t2; t3; ; tT1，其中 t1\ t2\ t3\\tT1构成 一个递减序列。那么我们可以定义 CJðv1;vkÞ ¼ ðVT; STÞ为从 V1到 VT的一条连通路径。

定义3：节点度d

如果节点Vi与汇聚节点Vs之间的连通路径数量为d，则d是节点Vi的节点度。相应地，可以提出平均节点度、最小节点度和k‐连通性的定义。该机会传 感器网络的平均节点度为N1d ¼ 1 N1 P dV i，其中N为节点数量，dv i是节点集 Vi中各节点的节点度。i¼1该机会传感器网络的最小节点度为dmin ¼ minðd1; d2; . . .; dN1Þ，若该网络的最小节点度 dmin ¼k，则该机会传感器网络是 k‐连通的。

定义4：连通性度 P1 H

h的连通性度可以定义为
P1 H ¼ 1
N1
i¼1
minðdVi ; LV i Þ
Tn
; Tn ¼ 1; 2;…; n ð1Þ
其中，N 是网络中的节点数量，dV i 是节点集Vi的节点度，LVi 是节点集Vi的时间片长度 累积值，minðdVi;LVi Þ 表示在 N 个时间片内汇聚节点接收到的消息数量，这些消息由节 点集Vi产生。

3.2 实验设置

在本节中，我们将介绍实验场景的详细信息以及通过应用公式（1）获得的实验 结果。首先，我们将介绍本实验中的场景及一些相关参数细节。然后，我们将 基于平均度验证网络连通性模型。
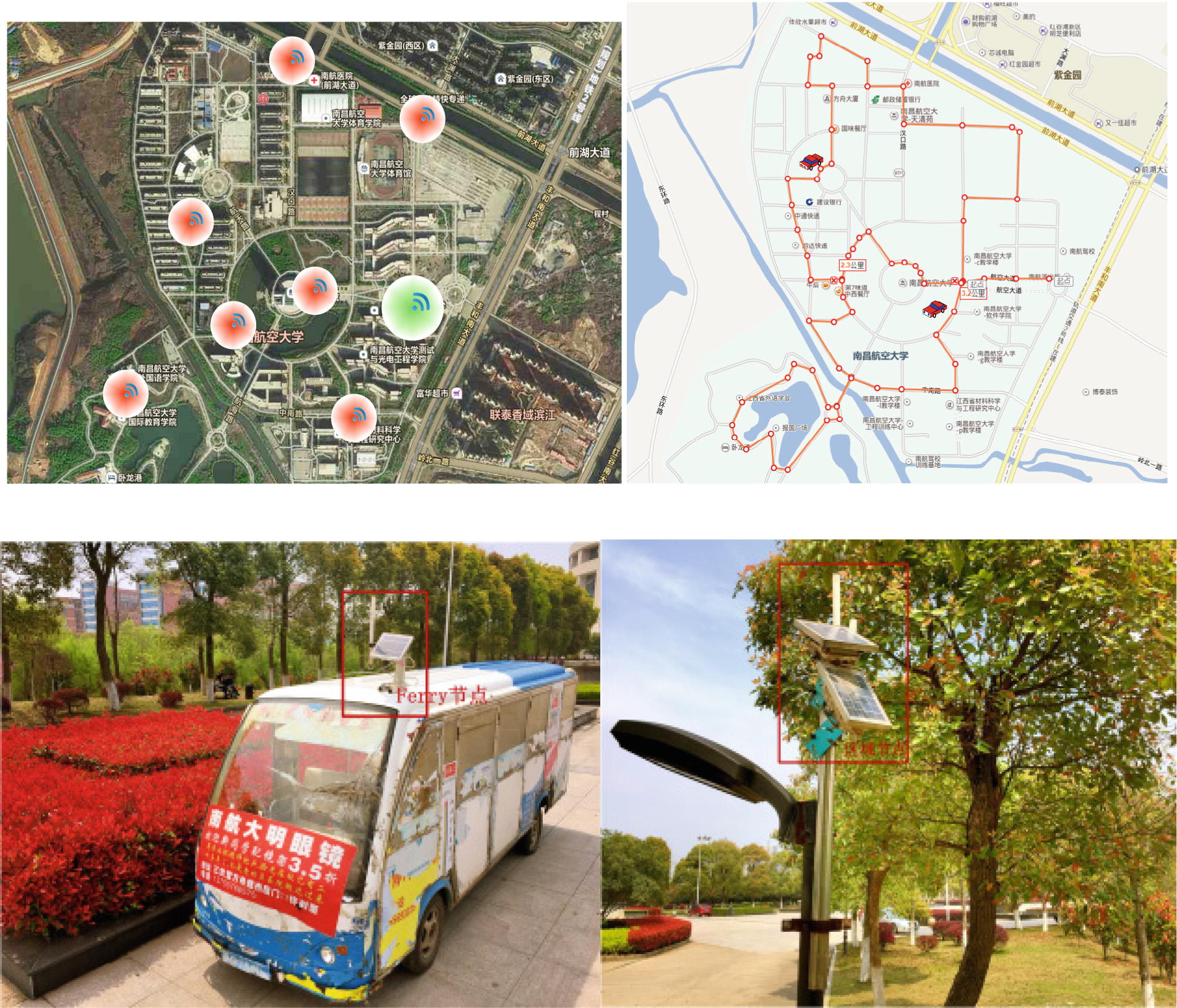
实验场景如图 3 所示。图 3(a) 是本实验中节点的分布情况，基于某学校的 卫星图像。绿色区域是汇聚节点的通信范围，红色区域是传感器节点的通信范 围。
学校内有两辆旅游巴士，用于接送学生从一个地方到另一个地方。如上图 Fig. 3(c)所示，我们将渡船节点部署在旅游巴士上，并在学校内部署了七个传 感器节点，如图Fig. 3(a)所示。这表明节点的分布非常广泛，节点之间无法直 接交换数据。这意味着节点只能通过渡船节点与其他节点交换数据。图Fig. 3(b)显示了渡船节点的一种可能的移动路径。本实验中有三种类型的传感器节 点：(i) 汇聚节点，(ii) 传感器节点，以及(iii) 渡船节点。我们在渡船节点中配 置了GPRS模式，以帮助我们追踪其路径，并将实验时间段设置为上午9:00至下 午7:00。本实验的参数详情见表Table 1。

节点分布)
渡船节点的轨迹)
渡船节点)
传感器节点)

参数	值
区域数量	7
渡轮节点数量	2
汇聚节点数量	1
区域节点采样周期	30 s
建模周期	5 分钟
滑动窗口长度 30 秒
采样时间	10 h
消息生存时间（TTL）	100 秒

3.3 网络连接度的验证

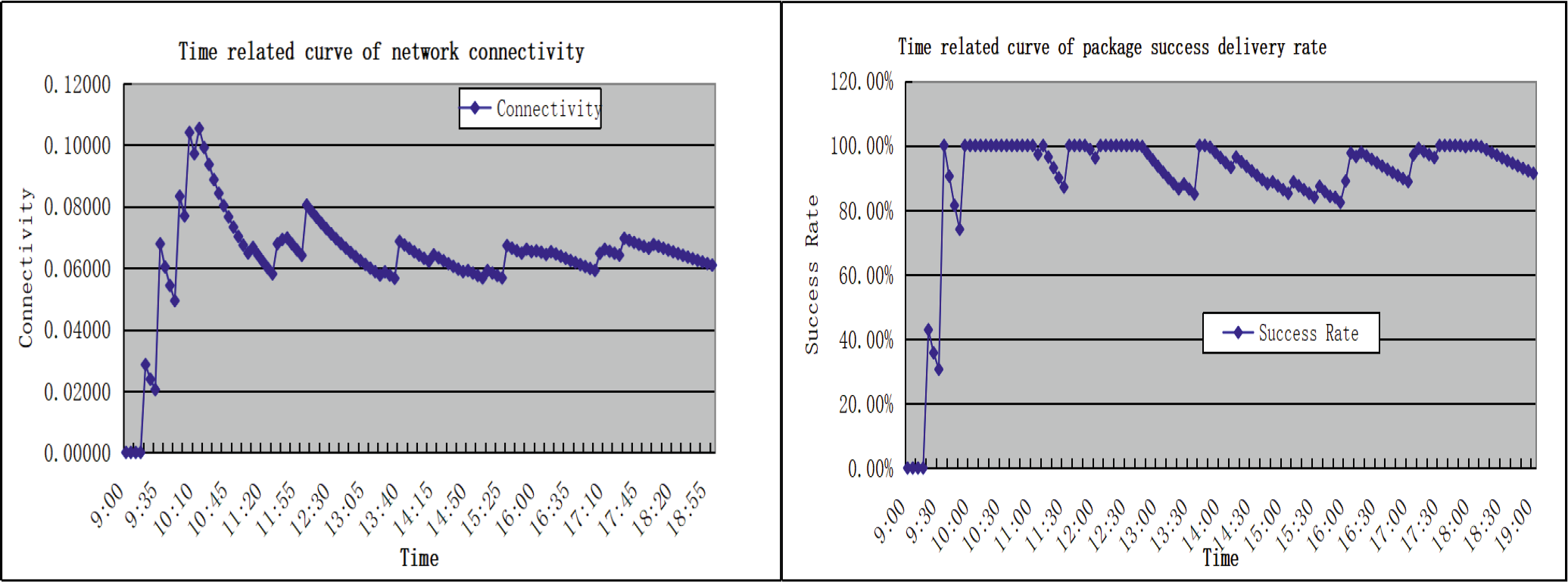
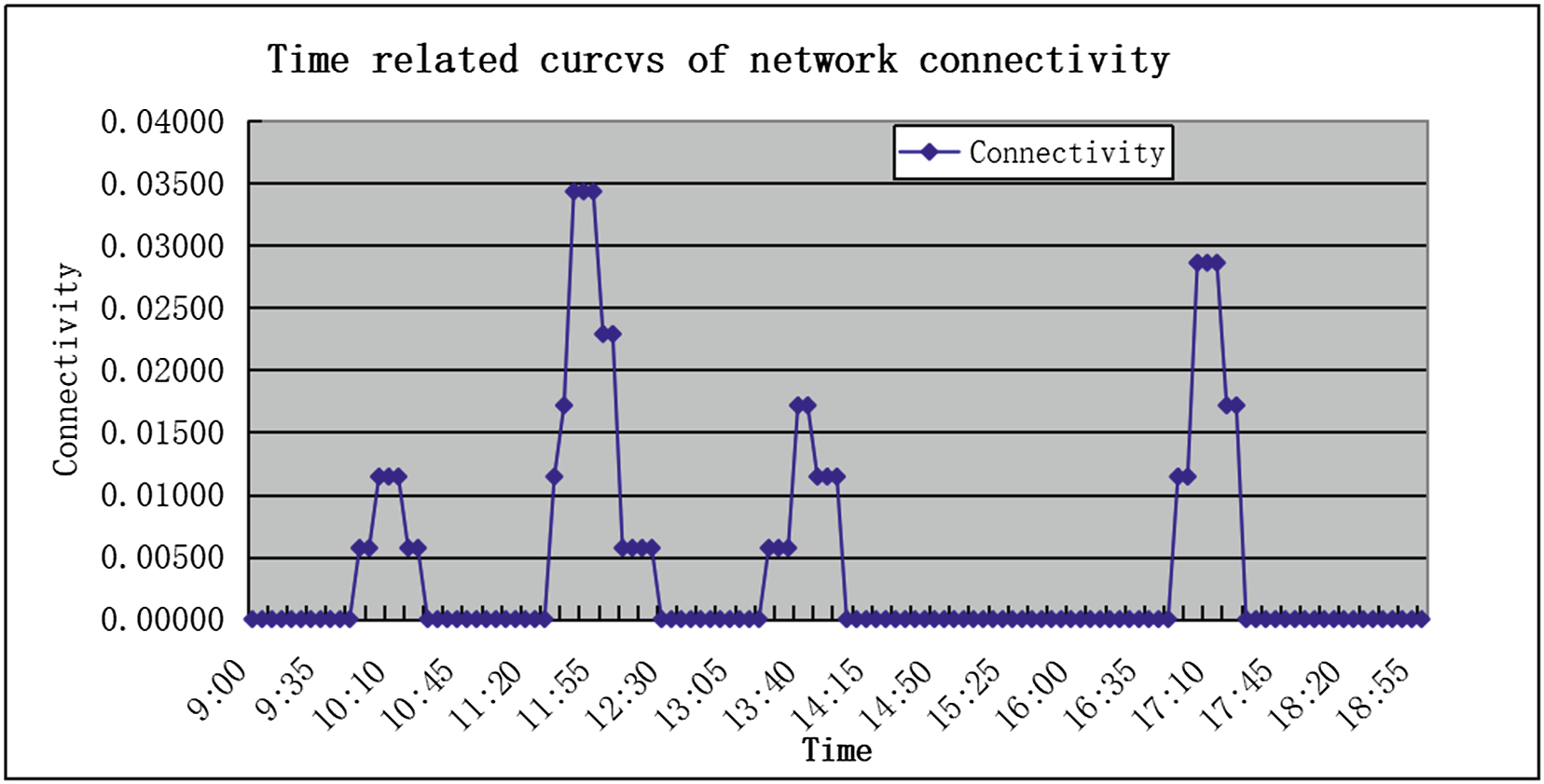
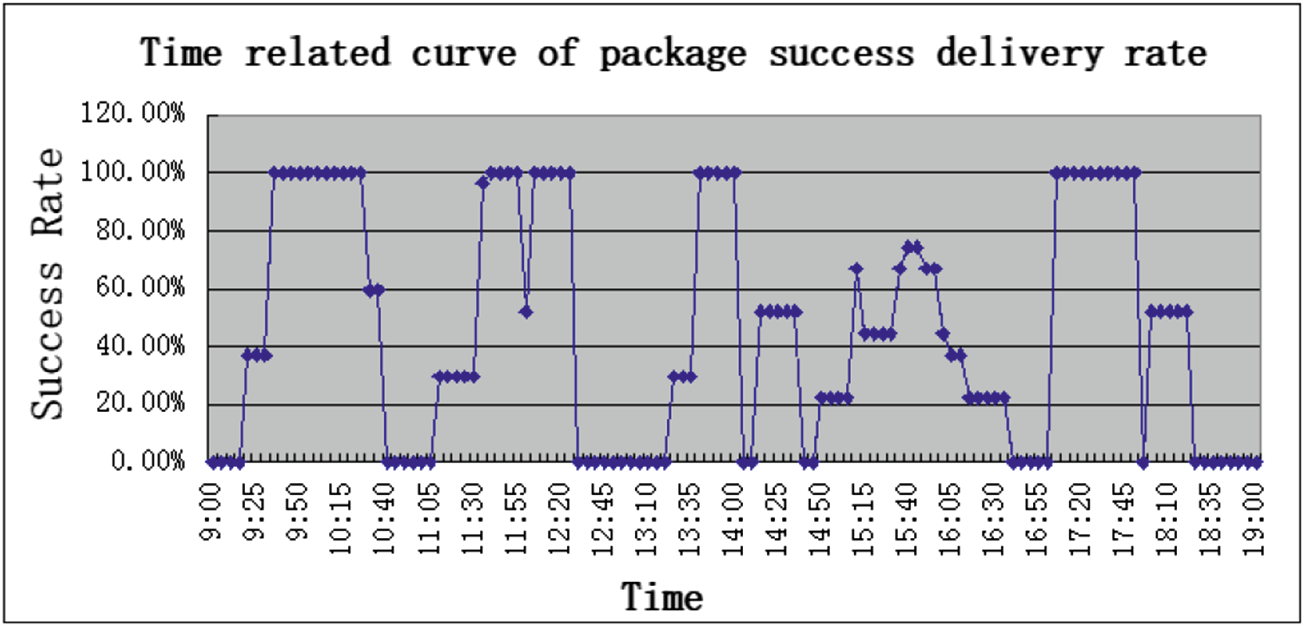
为了验证网络连通性，我们进行了实验，并得到了网络连通性与成功交付率的时间相关 曲线，如图 4和 5所示。
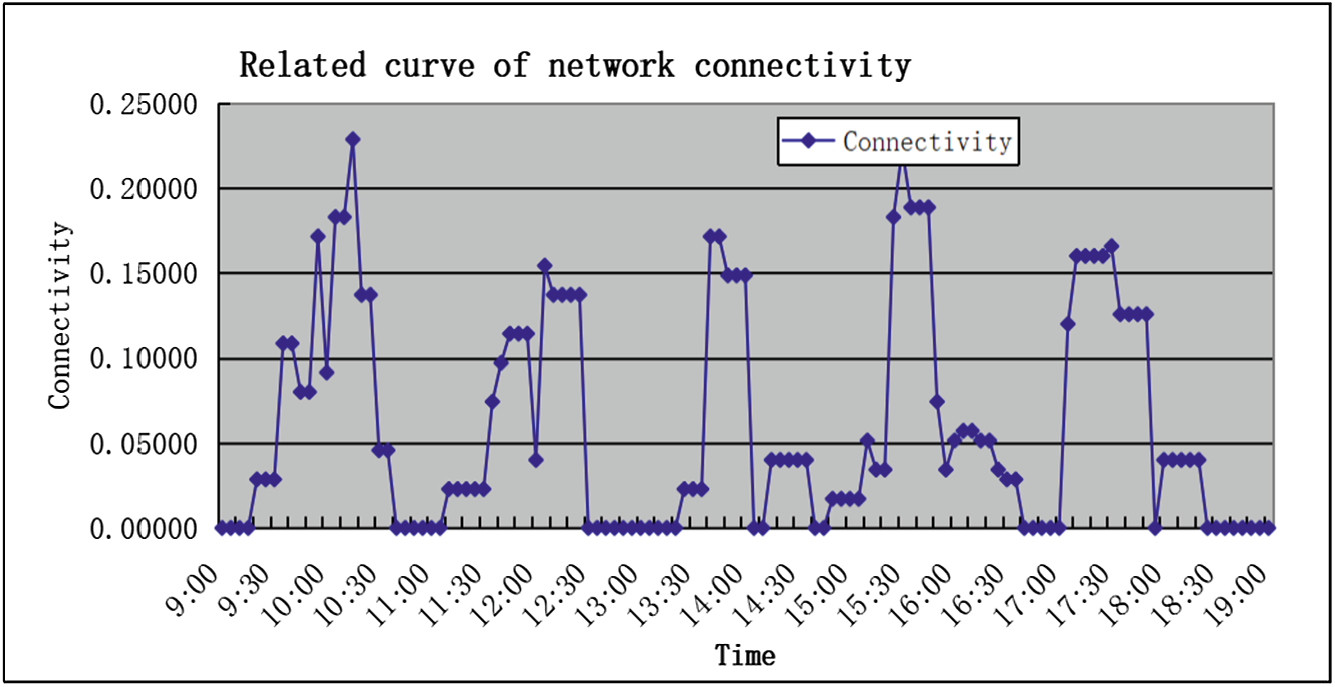
图4显示了在 10 小时内连通性趋势和包交付成功率的变化情况。可以看出， 连通性在约 10:15 达到峰值，之后逐渐下降。随后的四个峰值分别出现在接下 来的 11:30–12:00、13:35–14:00、15:30–15:50 和 17:00–18:00。从这些结果可 以看出，这些峰值出现在学生上课或下课的时间段。这与已知事实相符，因为 在这些时间段内，渡船节点的活动更加频繁，通信范围也更大。
另一方面，可以看出数据包成功投递率持续增长，并在10:15达到100%。
这是因为学生下课，渡船节点变得活跃，之后该比率在11:15后逐渐下降。随着 课程开始，渡船节点变得不活跃。需要提及的一点是，在15:00–15:40期间成功 率应该会上升，因为这是下课时间，渡船节点在此时应开始变得更加活跃。其 原因是我们在某一区域手动移除了一个天线，导致无法与渡船节点进行数据交 换。

4 分析与改进

在公式（1）中，网络连通性通过平均节点度来计算。因此，当一个传感器区域 的连通性降低到零时，其他区域的连通性可能增加，整个网络的连通性可能保 持不变或减少。这就是连通性趋势与图5中描述不符的原因。为了改进公式（1）， 本章提出了几种进一步的方法。

4.1 基于最小节点度的连通性度量

如上所述，平均节点度无法反映网络连通性的变化趋势，因为平均值只能反映 大多数节点的连通情况。为了克服这一不足，我们需要借鉴传统图论中的一些 思想。在传统图论中，若一个图是连通图，且其最小度为k [12]，则称该图为 k‐连通图。最小节点度的相关性表明，可以将节点度的最小值作为网络连通性， 而不是采用平均值。基于最小节点度的改进公式为：
P2 H ¼ min
minðdVi ; LV i Þ
Tn
; Tn ¼ 1; 2;…; n ð2Þ
其中，dVi是节点Vi的节点度，LVi是对应于Vi的所有时间序列的总和，Tn是从开始到 结束的快照数量。
本章使用公式（2）重新计算了网络连通性，结果如图6所示。结果表明， 在10:00–10:15、11:30–12:00、13:20–13:45和17:00–17:20期间，连通性呈上升 趋势，而在其他时间段则呈下降趋势。此外，由于移除了一根天线，导致一个 区域无法与其他区域通信，因此在15:00之后连通性开始下降。
这样，当某个区域的连通性下降甚至瘫痪时，网络连通性必然随之下降， 从而解决了公式（1）所提出的网络连通性无法反映少数区域瘫痪导致网络连通 性下降的问题。然而仍存在两个问题：第一，当网络连通性为零时，该方法无 法反映网络的瘫痪状态；第二，根据公式（2），该方法中的连通性仅与当前网 络中节点度最小的区域相关。因此，用该方法描述网络连通性具有片面性，无 法反映整体网络连通性。为了解决上述问题，我们将对该方法进一步改进。

4.2 滑动窗口与最小节点度

除了最小节点度外，LVi表示对应于节点集Vi的所有时间序列的总和，这意味着 minðdV i；当节点集Vi成功连接到另一个节点时，LV i Þ始终大于零。因此，即使 通过该方法网络中的所有节点都处于瘫痪状态，网络连通性也将呈现递减的双 曲线趋势，而不会变为零。为了解决这一问题，本文采用滑动窗口来选取部分 网络快照。因此，我们将把Tn限定为一个稳定数值，从而消除过时的快照带来 的影响。综上所述，计算公式将更新为：
P3 H ¼ min
minðdVi ; LV i Þ
TD
; TD ¼ n Dþ 1; n Dþ 2;…; n ð3Þ
其中TD ¼ n Dþ 1；n D þ 2；…；n，D 是滑动窗口的宽度，TD是其内的 快照数量。因此，网络连通性被限定在滑动窗口的时间段内，并将反映该滑动 窗口时间段内的网络连通性状态。
从图7可以看出，公式（3）不仅能在节点正常工作时恰当地反映网络连通 性状态，还能在12:40–13:20期间正确显示无网络连通性，此时天线已被移除。
然而在15:00–16:00期间，当我们移除某一区域的天线后，其余网络仍能正常工 作，但网络连通性却为零。这是因为在公式（3）中，网络连通性是通过最小节 点度和滑动窗口计算得出的。这意味着只要有一个节点无法与任何其他节点建 立连接，整个网络就会瘫痪，这与实际情况不符。

4.3 滑动窗口的进一步改进

为解决该问题，本文采用平均节点度代替最小节点度，以增强模型的鲁棒性。 因此当部分节点发生瘫痪时，网络连通性会下降，但不会变为零。以下是改进 后的公式，其中N表示网络中的节点数量：
P4 H ¼ 1
N1
i¼1
minðdVi ; LV i Þ
TD
; TD ¼ n Dþ 1; n Dþ 2;…; n ð4Þ
在图8中，5:00–16:00期间，网络消息的成功投递率低于其他四个高峰期， 因为在该时间段内我们移除了某个区域的一根天线，导致成功投递率下降。而 在图9中，15:00–16:00期间出现了一个较高的峰值，连通性明显优于其他时段， 这与实际情况不符。

4.4 基于多属性决策树的连通性模型 e

根据上述公式，可以推断出机会传感器网络的连通性具有复杂性和多变性。很 难用一个简单的公式描述所有的特征。因此，为了建立一个计算连通性的综合 模型，本文提出了一种基于多属性决策树的方法，并将网络连通性的每个特征 视为决策树的一个属性。首先，机会传感器网络的状态可分为以下三种主要情 况：“完全断开的网络”、“部分连通的网络”或“完全连通的网络”。
1. 完全断开的网络：无网络连通性意味着整个网络完全瘫痪。我们可以通过使 用公式（4）来验证最终的连通性结果是否为零。连通性为零意味着没有网络连 通性；
2. 部分连通的网络：部分节点相连意味着网络中的某些区域是可工作的，我们 可以使用公式（3）来证明这一点。如果应用公式（3）的结果大于零，则网络 完全正常运行且没有任何断裂的节点，否则将存在一些无法相互交换数据的区 域。为了更具体地研究这种情况，我们可以使用公式（5）来评估最终结果是否 大于或等于零：
dP4 H
¼ d 1
N1
i¼1
minðdVi ; LV i Þ
TD
!
; TD ¼ n Dþ 1; n Dþ 2;…; n ð5Þ
公式（5）与公式（4）不同，因为它表示网络连通性趋势。如果公式（5） 的结果大于零，则可以推断连通性趋势为正且在增加；当结果为零时，连通性 稳定；否则，本文认为当结果小于零时，连通性不合格。
3. 完全连通的网络：具有完全连通的网络意味着网络中的所有节点都被激活， 并且每对不同的顶点都通过唯一节点相连。在上述情况下，本文仍然使用公式 （5）将网络状态分类为‘良好’、‘一般’或‘不合格’。
总之，连通性的状态可以分为从零到六：
• S0：完全断开的网络—0；• S1：部分连通的网络且连通性趋势为“不合格”— 1；• S2：部分连通的网络且连通性趋势为“一般”—2；• S3：部分连通的网 络且连通性趋势为“良好”—3；• S4：完全连通的网络但连通性趋势为“不合 格”—4；• S5：完全连通的网络但连通性趋势为“一般”—5；• S6：完全连 通的网络但连通性趋势为“良好”—6；
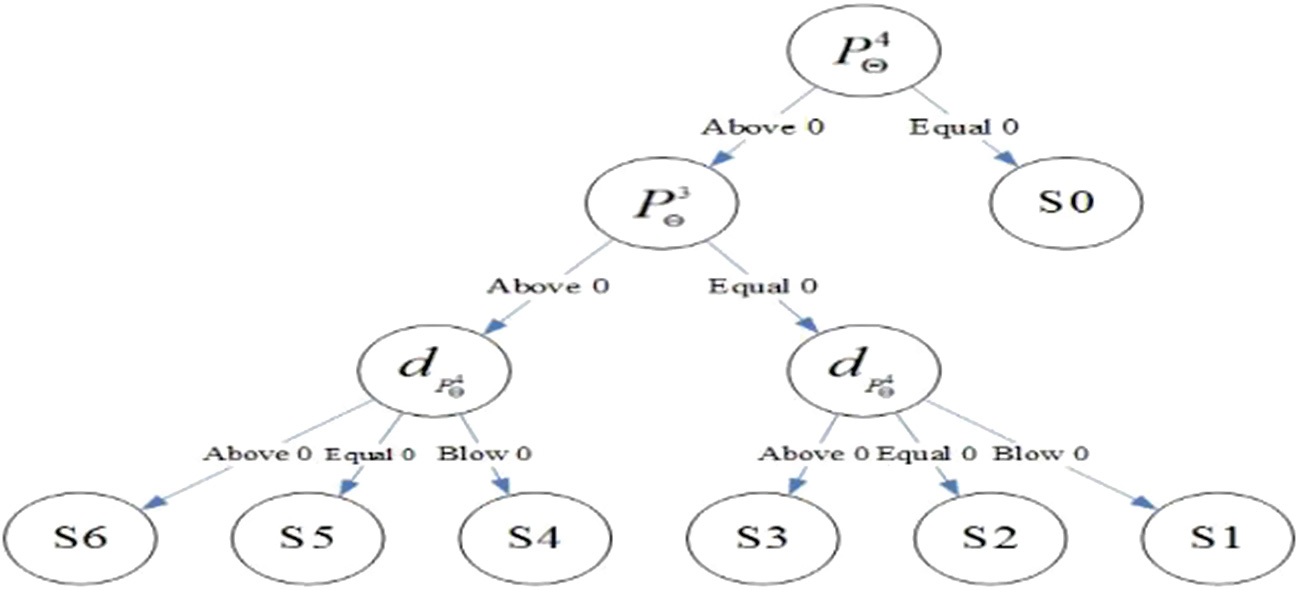
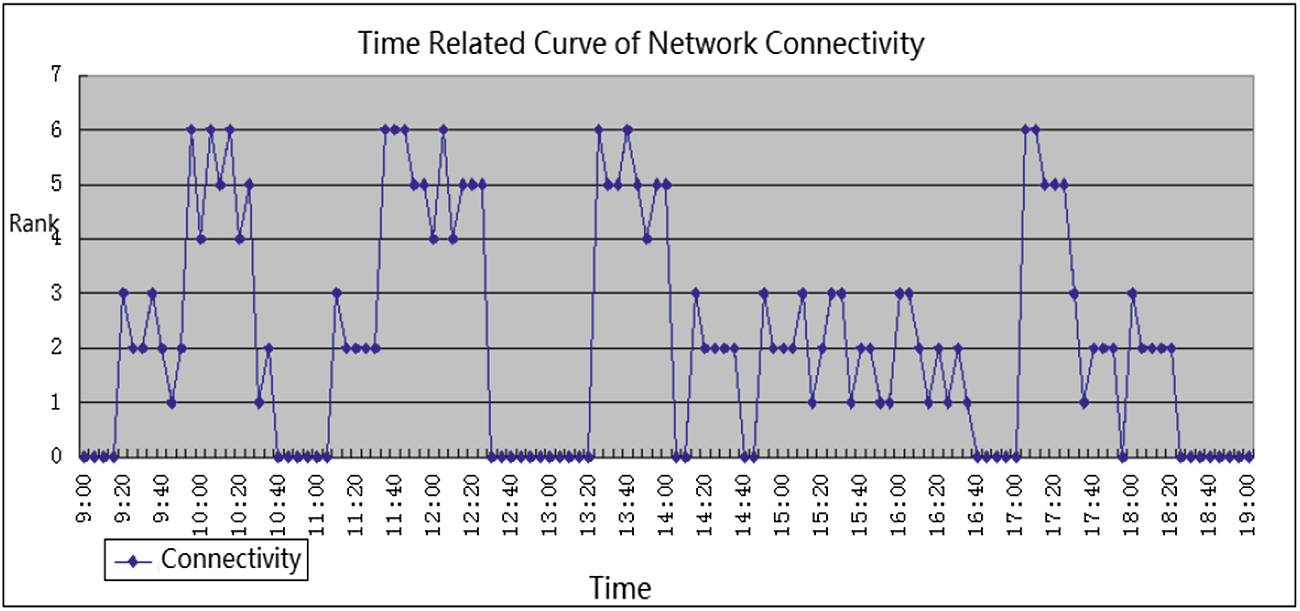
根据由公式（3）计算得到的P3 H、由公式（4）计算得到的P4 H以及由公式（5） 计算得到的dHP4，如图10所示的多属性决策树和基于多属性决策树的实验数据如图 11所示：

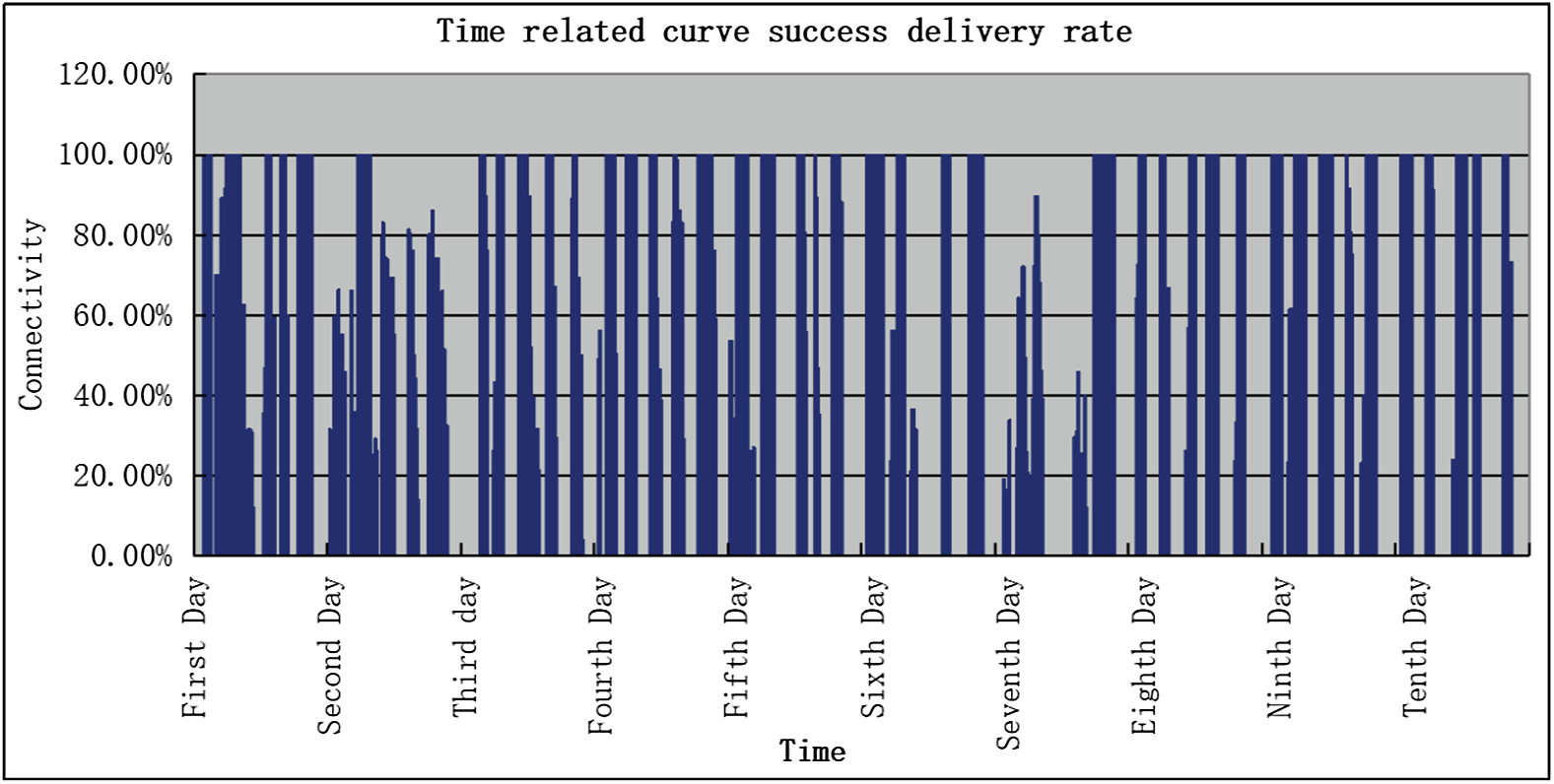
为了验证多属性决策树模型的准确性，本文将实验扩展到10天，并基于多 属性决策树收集了100小时的数据。图12中的实验结果。
从图12可以看出，第二天的网络连通性比其他天少。这是由于某个区域内 的节点电压不足所致。我们还可以发现，第七天的峰值数量比其他天少。这是 因为工作日只有一辆旅游巴士，而其他工作日有两辆旅游巴士。因此，图12符 合实际情况。这意味着多属性决策树相比其他方法能更真实、全面地反映网络 连通性。

5 结论

机会传感器网络的连通性具有时间相关性和演化性。本文指出了传统连通性模 型的缺点，并通过实验加以证明。然后，提出了四种不同方法来改进连通性模 型，同时比较了它们的优缺点。最后，本文采用多属性决策树模型来改进连通 性模型，并利用该方法取得了满意的结果。实验表明，多属性决策树模型能够 反映连通性的不同状态水平，并在监控过程中最小化误差。未来，本文将进一 步考察多属性决策树模型的准确性，并针对相同的优先级水平进一步优化分类。