灰狼优化双向长短期记忆网络(GWO-BiLSTM)在回归预测和时序预测中的应用及参数优化，基于灰狼优化的GWO-BiLSTM网络在回归和时序预测中的应用及参数优化研究

GWO-BiLSTM 双向长短期记忆网络
基于灰狼优化双向长短期记忆网络(GWO-BiLSTM)的回归预测或时序预测
优化参数为学习率，隐藏层节点个数，正则化参数。
matlab代码

ID:4649681999313536

从深海遇见你

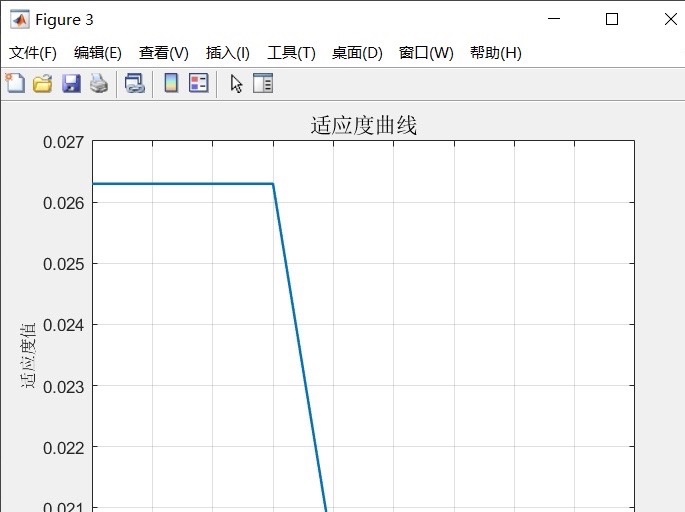
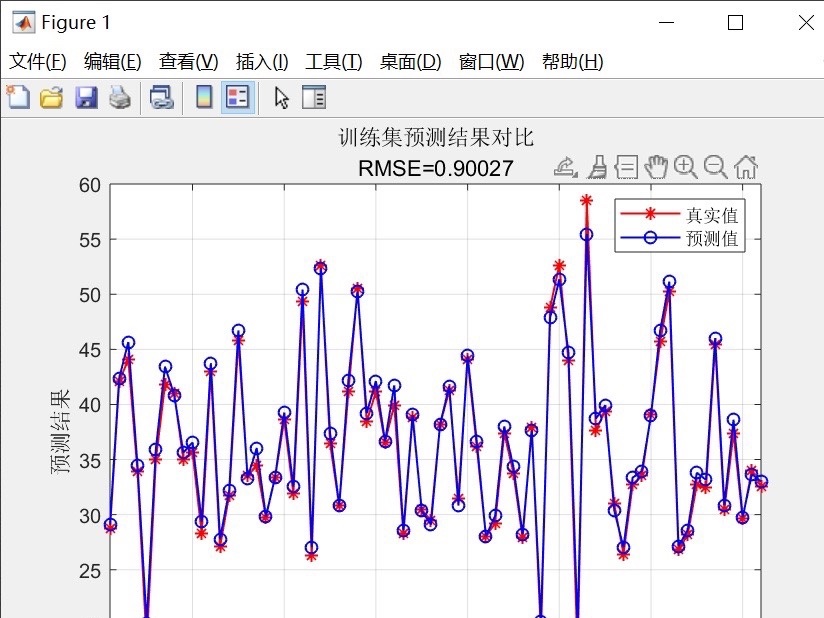
GWO-BiLSTM 双向长短期记忆网络(GWO-BiLSTM) 是一种基于灰狼优化的回归预测或时序预测方法，旨在优化网络参数，包括学习率、隐藏层节点个数和正则化参数。本文将详细介绍GWO-BiLSTM的原理和应用，并提供了相应的Matlab代码。

首先，我们需要了解双向长短期记忆网络(BiLSTM)。LSTM是一种循环神经网络(RNN)的变种，通过引入门控结构，解决了传统RNN在长序列训练中的梯度消失和梯度爆炸问题。而BiLSTM则通过在网络中引入正向和反向两个方向的LSTM单元，提高了对序列数据的建模能力。

而GWO是一种基于群体智能的优化算法，模拟了灰狼群体在求解问题时的行为。灰狼优化算法通过模拟灰狼个体之间的协作与竞争，实现了全局寻优的目标。

接下来，我们将GWO与BiLSTM相结合，构建GWO-BiLSTM模型。首先，我们需要确定网络的结构，包括隐藏层的节点个数和正则化参数。隐藏层节点个数的选择需要根据具体问题的复杂程度和计算资源来确定。正则化参数则用于控制模型的复杂度，避免过拟合问题的发生。这些参数的优化将通过GWO算法来实现。

在GWO-BiLSTM中，首先利用GWO算法搜索最佳参数，通过调整学习率、隐藏层节点个数和正则化参数，提高模型的拟合能力和预测准确度。然后，将优化后的参数应用于BiLSTM网络中，进行回归预测或时序预测。

代码实现方面，我们提供了Matlab代码供读者参考。该代码包括了GWO算法的实现和BiLSTM网络的搭建。读者可以根据自己的需求进行参数设置和数据加载，然后通过调用相应的函数完成模型训练和预测。

在实际应用中，GWO-BiLSTM可以用于各种回归预测或时序预测的任务，如股票价格预测、天气预测等。通过优化网络参数和结构，GWO-BiLSTM能够提高模型的性能和泛化能力。

总结起来，本文介绍了GWO-BiLSTM双向长短期记忆网络的原理和应用。通过灰狼优化算法优化网络参数，提高模型的性能和泛化能力。同时，我们提供了Matlab代码供读者参考。通过将GWO-BiLSTM应用于回归预测或时序预测任务中，可以有效解决实际问题。希望这篇文章能够对读者在技术分析方面提供一定的帮助和启发。

注意：本文的目的是展示技术分析和阐述算法原理，不涉及价格、退货、售后等商业问题。

相关的代码,程序地址如下：http://fansik.cn/681999313536.html