poj1189

原创于 2018-12-02 20:43:43 发布 · 212 阅读

CC 4.0 BY-SA版权

这题其实是一个用dp来模拟的题，技巧挺多，坑也挺多的。

一直想着直接用分数计算，但精度不够。于是假设有2^n个球掉下来，看最后落在格挡内有几个球就行了！！！

简单的原因是在讨论点(i,j)的时候，第二种方法只有dp[i][j]，但是第一种还有dp[i][j+1]，又因为i和j是从小到大的，所以在(i,j)时，(i，j+1)还没有讨论出来，所以他的dp值此时为0，有点棘手。所以第二种转换好，但是需注意，这里是+= ！！！

在这种情况下，大部分变量都要定义成long long形式，因为2^50会溢出。

这里dp[i][j]的i，j要从0开始，因为这里默认第个m格子就是dp[n][m]，所以是将格子也看做是钉子了，但是原本就有n层，所以应该从0开始。

i的范围不要包括n在内。不是因为会错，而是因为没有意义。特别是我这里边输入边处理，所以是不允许取等号。

这两种写法上面（1）是对的，下面（2）是错的。

在int范围内，（2）也是对的，但是到了long long以后就会溢出。

因为：

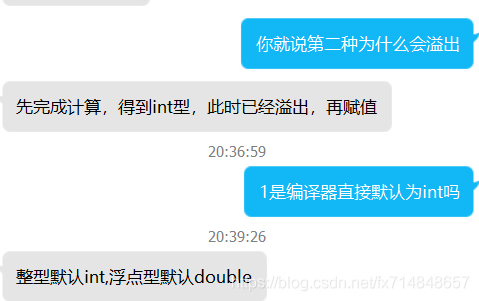
代码：

//poj1189
#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
#define MAXN 55
typedef long long LL;

LL dp[MAXN][MAXN];//dp[i][j]表示球落到在点（i,j）处的概率，但是在这题巧妙地转换成了能落到这个点的球的个数，避免了分数运算
LL Map[MAXN][MAXN];

LL GCD(LL a,LL b)
{
    if(b==0)
        return a;
    return GCD(b,a%b);
}

int main()
{
    int i,j;
    int n,m;
    char temp;
    LL allnum;
    LL gcd;

    while(cin>>n>>m)
    {
        allnum=(LL)1<<n;
        //allnum=1 << n;
        memset(dp,0,sizeof(dp));
        dp[0][0]=allnum;
        for(i=0;i<n;i++)
        {
            for(j=0;j<=i;j++)
            {
                cin>>temp;
                if(temp=='*')
                {
                    dp[i+1][j]+=dp[i][j]/2;
                    dp[i+1][j+1]+=dp[i][j]/2;
                }
                else
                    dp[i+2][j+1]+=dp[i][j];
            }
        }
        gcd=GCD(allnum,dp[n][m]);
        printf("%lld/%lld\n",dp[n][m]/gcd,allnum/gcd);
        //cout<<dp[n][m]/gcd<<"/"<<allnum/gcd<<endl;
    }
    return 0;
}