poj1322 概率dp（蜜汁优化技巧）

题目：

https://vjudge.net/problem/POJ-1322

 

这题是一道很普通的概率dp题目，但是如果不进行剪枝就会超时，而这题用的剪枝恰恰非常巧妙。

 

首先是思路分析：

当i+j时奇数还是偶数这个分析确实很难想到。（当然，没有这个条件也可以AC的）

 

而关于处时输入数据是否满足题目条件的判断就比较套路。

这个条件其实是对时间和空间同时进行优化，时间是for循环的次数，空间是dp数组的大小。

因为这题的M<=C是肯定的，所以只要开到110，但是如果没有这个剪枝，那么M>100时会越界。

 

关于dp的初始化是非常重要的，否则会得到所有数组的值都是0。而这里的初始化是dp[0][0]=1。（按照逻辑，dp[1][1]也是=1，但是i是从1开始的，而且j是从0开始的，而且开始的时候就要用到上一层的数组值，所以必须从（0,0）开始初始化）。

 

关于dp数组的定义：

double dp[2][MAXN];//dp[i][j]表示在操作了i次（取了i颗糖）后，桌面上剩余的巧克力的数量为j
这里用了滚动数组，数组第一维只有2个空间，而没有直接将他压缩成为1维数组，是因为：

dp[i][j]会同时用到dp[i-1][j-1]和dp[i-1][j+1]，而dp[i][j+1]会用到dp[i-1][j]和dp[i-1][j+2]，两个压缩一下就变成：

dp[j]=dp[j-1]*...+dp[j+1]*...和dp[j+1]=dp[j]*...+dp[j+2]*....，这时无论怎么调整for循环中的i和j的顺序都不能保证不覆盖，所以必须用二维数组。

 

最后是关于这一步：

因为最后输出结果时决定是奇数还是偶数，所以N=1000还是1001要判断。

因为只要三位小数，精度很低，所以1000次运算足矣（证明不清楚）

 

还有另一种方法：

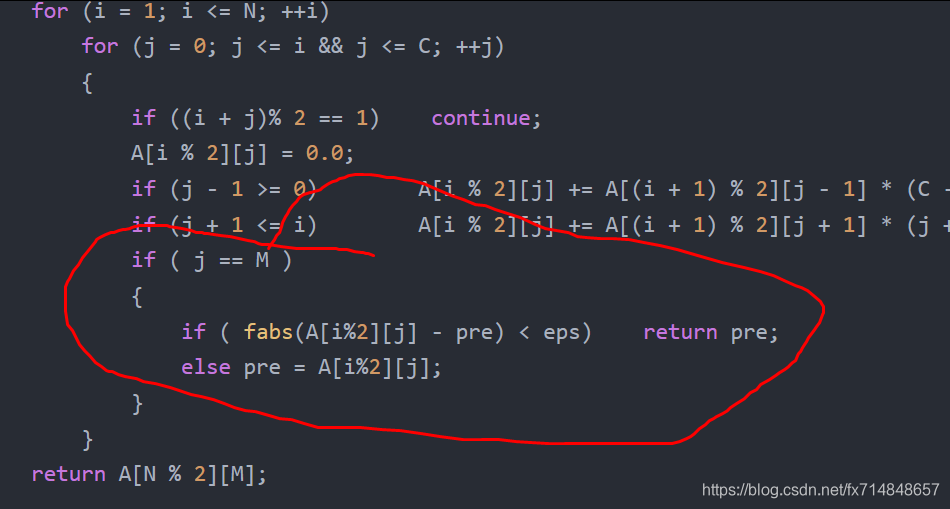
方法来自：https://blog.youkuaiyun.com/non_cease/article/details/6895083

 

我的代码：
 

//poj1322
#include<stdio.h>
#include<string.h>
#define MAXN 110

double dp[2][MAXN];//dp[i][j]表示在操作了i次（取了i颗糖）后，桌面上剩余的巧克力的数量为j

int main()
{
    int i,j;
    int C,N,M;
    int temp;

    while(scanf("%d",&C)&&C)
    {
        scanf("%d%d",&N,&M);
        memset(dp,0,sizeof(dp));
        dp[0][0]=1.0;
        if(M>100||M>C||M>N)
        {
            printf("%.3f\n",0.0);
            continue;
        }
        temp=N;
        if(N>1000)
            N=1000+(N%2);
        for(i=1;i<=N;i++)
        {
            for(j=0;j<=i&&j<=C;j++)
            {
                /*if((i+j)%2!=0)
                    dp[i%2][j]=0;
                else*/
                    dp[i%2][j]=dp[(i-1+2)%2][j-1]*((C-j+1)*1.0/C)+dp[(i-1+2)%2][j+1]*((j+1)*1.0/C);
                if(i==N&&j==M)
                    break;
            }
            if(i==N)
                break;
        }
        printf("%.3f\n",dp[temp%2][M]);
    }
    return 0;
}