优雅的暴力：替罪羊树

前言

本文无大错误不再更新，会更新在博客。

默认读者会 BST 的基本操作。

节点定义

替罪羊树采用了懒惰删除的方法，不会立即删除某个点，而是在重构时不放进数组。

struct node{  

    int ch[2], val;  

    int siz1, siz2, cnt, sum;  

    //扣去懒惰删除的节点数量，没扣去懒惰删除的节点数量，树内相同权值的数量，子树大小。  

}d[N];  

int root, tot, stk[N], top, v[N], t;//stk 是垃圾回收  

double al = 0.75;  

#define ls(x) d[x].ch[0]  

#define rs(x) d[x].ch[1]  

int newnode(int x){  

    int w = top ? stk[top--] : ++tot;  

    return d[w].val = x, ls(w) = rs(w) = 0, d[w].cnt = 1, pushup(w), w;  

}  

void pushup(int x){  

    node&rt = d[x],ls = d[ls(x)],rs = d[rs(x)];  

    rt.siz1 = (rt.cnt > 0) + ls.siz1 + rs.siz1;  

    rt.siz2 = 1 + ls.siz2 + rs.siz2;  

    rt.sum = rt.cnt + ls.sum + rs.sum;  

}  

重构

BST 最担心的是树退化成链。

那么有个暴力的想法：

把树拍扁放进数组，然后重新构建一棵完全二叉树。

但是过多的重构会使复杂度上升，那么我们引入一个概念：$\alpha$

$\alpha = \dfrac{\max(siz2_{ls}, siz2_{rs})

}{siz2_{rt}}$

一般的平衡树都能把 $\alpha$ 维护在 $[0.6,0.8]$ 左右。

我们可以将 $\max \alpha$ 设为一个数，一般为 $[0.7,0.8]$。

一般选 $0.75$。

在某个节点的 $\alpha >\max \alpha$ 时，我们把这个子树重构。

如果这个树 $siz1\le \alpha siz2$，那么我们认为它也是需要重构的。

比如这棵树：

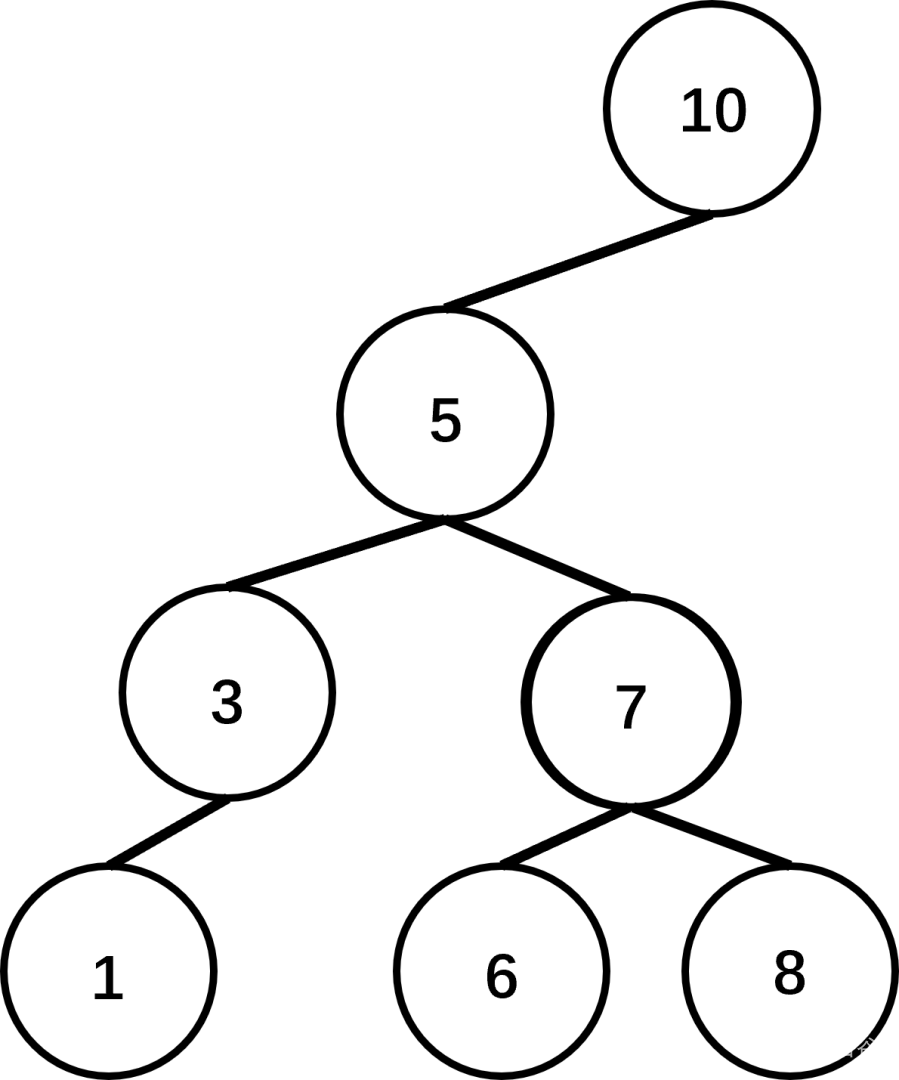
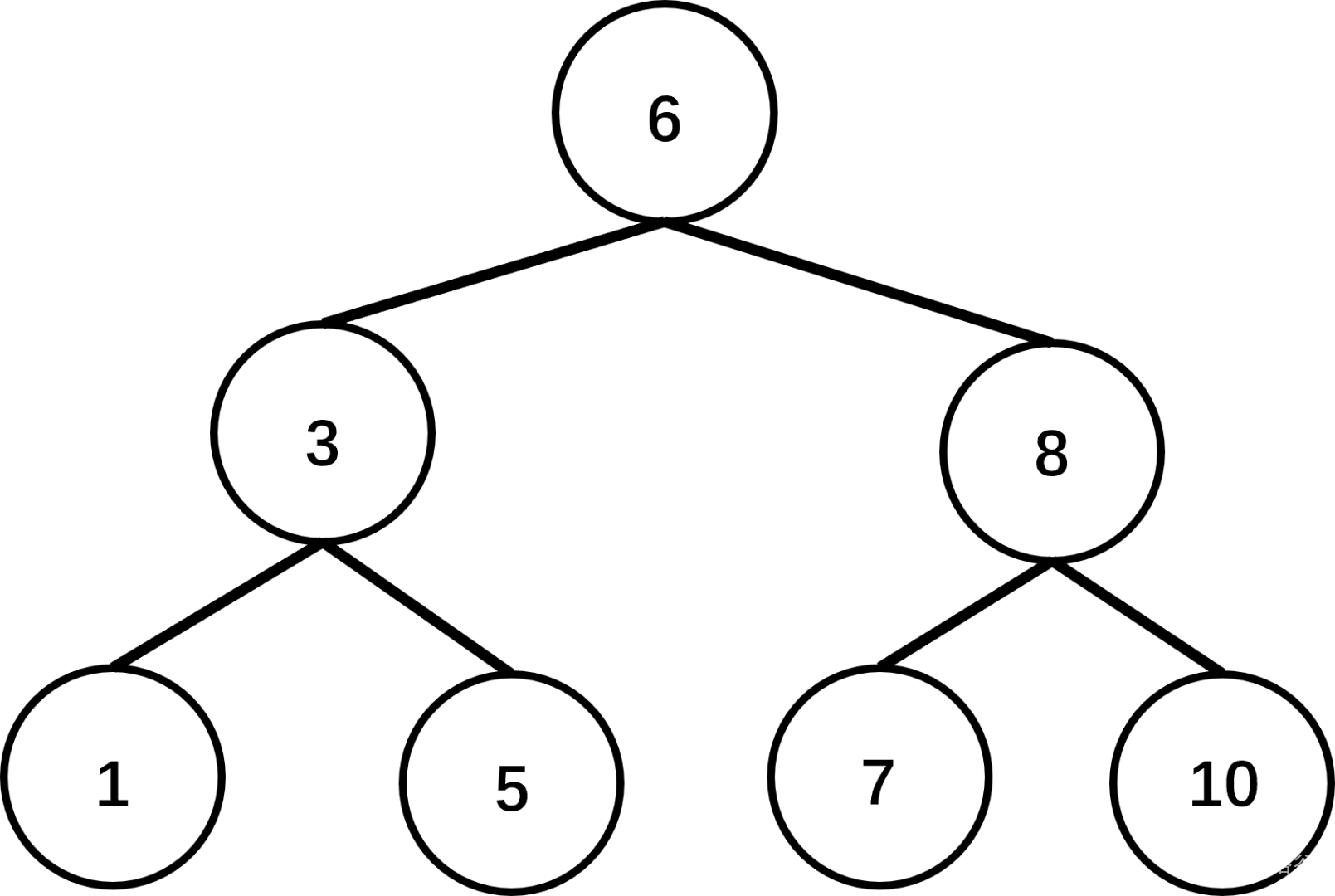
那么我们将它拍扁放进数组。

然后像线段树一样重新建树。

#define check(x) x&&(al*d[x].siz2<=max(d[ls(x)].siz2,d[rs(x)].siz2)||d[x].siz1<=0.75*d[x].siz2)  

void dfs(int x){  

    if(!x)return;  

    dfs(ls(x)), (d[x].cnt ? v[++t] : stk[++top]) = x, dfs(rs(x));  

}  

int build(int l, int r){  

    if(l == r)return ls(v[l]) = rs(v[l]) = 0, pushup(v[l]), v[l];  

    if(l > r)return 0;  

    int mid = l + r >> 1, x = v[mid];  

    ls(x) = build(l, mid - 1), rs(x) = build(mid + 1, r);  

    return pushup(x), x;  

}  

#define refactoring(x) t = 0, dfs(x), x = build(1, t)  

插入

如果在当前节点的权值和要插入的权值一样，我们将 $cnt$ 增加。

其他和 BST 一样。

记得在回溯时更新节点，判断是否重构。

void insert(int&now, int val){  

    if(!now)return void(now = newnode(val));  

    if(d[now].val == val)d[now].cnt++;  

    else if(d[now].val < val)insert(rs(now), val);  

    else insert(ls(now), val);  

    pushup(now);  

    if(check(now))refactoring(now);  

}  

删除

懒惰删除，只是将 $cnt$ 减少。

然后在回溯时更新节点，判断是否重构。

void del(int&now, int val){  

    if(!now)return;  

    if(d[now].val == val)d[now].cnt--;  

    else if(d[now].val < val)del(rs(now), val);  

    else del(ls(now), val);  

    pushup(now);  

    if(check(now))refactoring(now);  

}  

查询操作

这部分就差不多了。

int kth(int x){  

    int now = root, siz = 0, z = x;  

    while(now){  

        if((siz = d[ls(now)].sum) >= x)now = ls(now);  

        else if((siz += d[now].cnt) < x)x -= siz, now = rs(now);  

        else return d[now].val;  

    }  

    return -1;  

}  

int query_rank(int val){  

    int ans = 1, now = root;  

    while(now){  

        if(d[now].val == val)ans += d[ls(now)].sum, now = 0;  

        else if(d[now].val < val)ans += d[ls(now)].sum + d[now].cnt, now = rs(now);  

        else now = ls(now);  

    }  

    return ans;  

}  

int ask_pre(int val){return kth(query_rank(val) - 1);}  

int ask_next(int val){return kth(query_rank(val + 1));}  

代码

完整代码。