前言
个人博客。
fhq-treap 又名“无旋 treap”,有着码量小,易理解,可持久化等特点。
但 fhq-treap 的常数较大。
必要:
-
堆。
选要:
基础操作
treap 的每个节点都有一个随机的优先级。
treap 的权值要具有二叉搜索树的性质,优先级满足堆的性质。
fhq-treap 有两个关键函数 split 和 merge,分别是分裂和合并。
代码中均为小根堆。
节点
在 fhq-treap 中我们需要维护子树大小,节点权值,左右儿子,优先级(随机数,用于堆)。
std::mt19937 rd(std::chrono::steady_clock::now().time_since_epoch().count());
//需要 random 和 chrono 头文件,不要放在结构体内
struct node{
int size, val, rank, ls, rs;
}d[N];
int tot = 0, root = 0;
int newnode(int val){
d[++tot].val = val, d[tot].rank = rd();
d[tot].size = 1, d[tot].ls = d[tot].rs = 0;
return tot;
}
void getsize(int u){d[u].size = 1 + d[d[u].ls].size + d[d[u].rs].size;}
分裂
按权值分裂
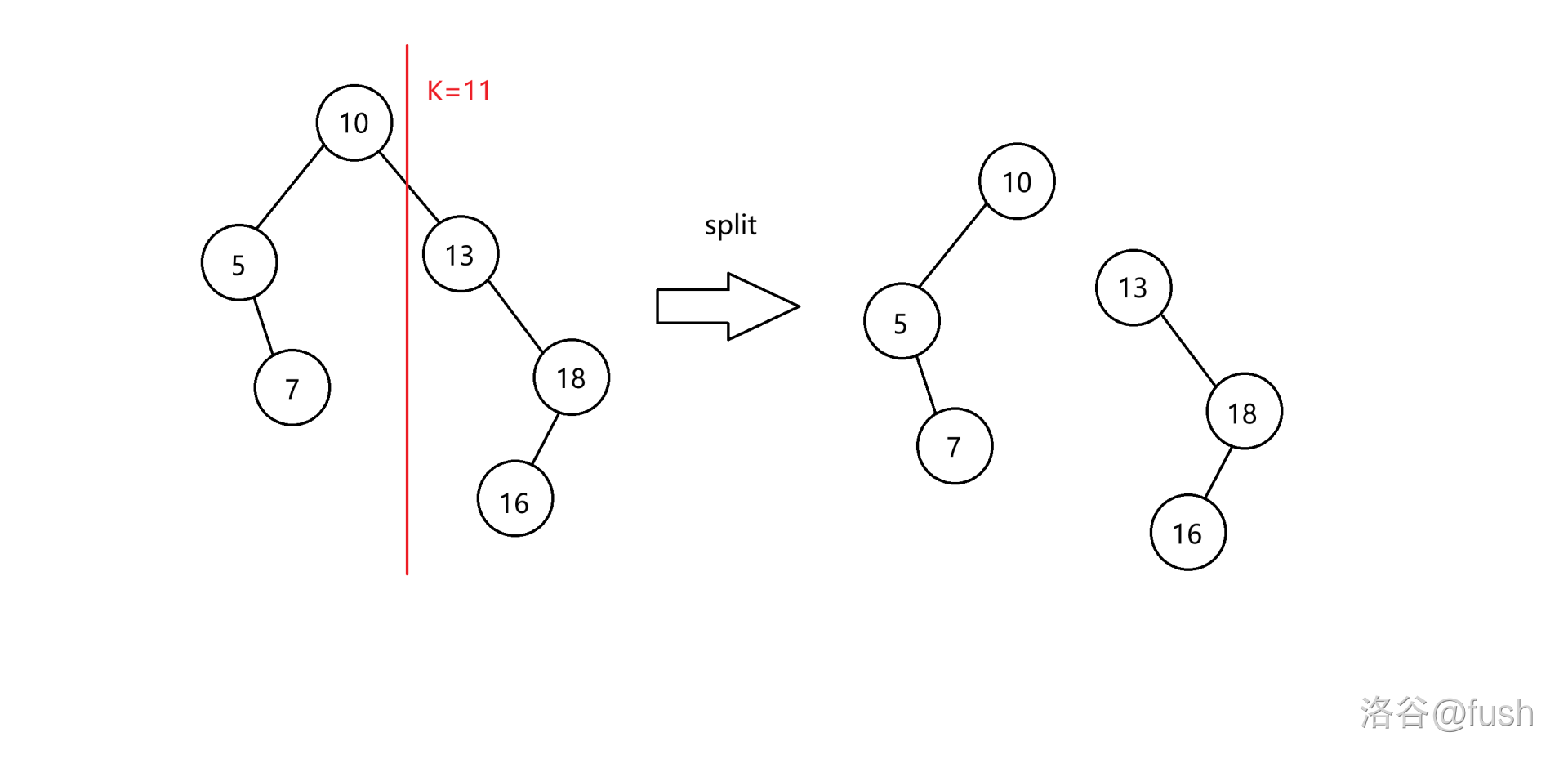
明显,我们会把一个树,把权值 ≤ k \le k ≤k 的放在 L L L 树中, > k > k >k 的放在 R R R 树中。
void SplitVal(int now, int val, int&L, int&R){
if(!now)return void(L = R = 0);
if(d[now].val <= val)L = now, SplitVal(d[now].rs, val, d[now].rs, R);
else R = now, SplitVal(d[now].ls, val, L, d[now].ls);
return getsize(now);
}
我们理解一下代码。
我们现在遍历到了原树的 n o w now now 节点。
如果节点是空的那么 L L L 和 R R R 树都是空的。
如果这个节点的权值 ≤ k \le k ≤k:
那么我们把他放在 L L L 树中,然后行对 n o w now now 节点的右儿子遍历。
由于是二叉搜索树,所以 n o w now now 的左儿子的权值均 ≤ k \le k ≤k。
所以只用考虑分割 n o w now now 的右儿子的是在 L L L 树的右儿子,还是在 R R R 树内。
反之同理。
按排名分裂
同理,只不过要判断左子树的大小关系。
void SplitRank(int now, int k, int&L, int&R){
if(!now)return void(L = R = 0);
int size = d[d[now].ls].size;
if(k <= size)R = now, SplitRank(d[now].ls, k, L, d[R].ls);
else L = now, SplitRank(d[L].rs, k - size - 1, d[L].rs, R);
getsize(now);
}
合并
合并是分裂的逆操作,我们回到之前的这幅图。

如果要合并,我们需要保证 ∀ x ∈ L , y ∈ R , v a l ( x ) ≤ v a l ( y ) \forall x \in L, y \in R, val(x) \le val(y) ∀x∈L,y∈R,val(x)≤val(y)。
由于两棵树有序,只需要根据优先级考虑哪颗树放“上面”,哪棵树放“下面”,即考虑哪棵树成为子树。
同时,我们还需要满足二叉搜索树的性质。
所以若 L L L 的根结点的优先级 < R < R <R 的,则 L L L 成为根结点,由于 R R R 的权值 ≥ L \ge L ≥L,所以 R R R 和 L L L 的右子树合并。
反之,则 R R R 作为根结点, L L L 和 R R R 的左子树合并。
int merge(int L, int R){
if(!L || !R)return L + R;
if(d[L].rank < d[R].rank){
d[L].rs = merge(d[L].rs, R), getsize(L);
return L;
}
else {
d[R].ls = merge(L, d[R].ls), getsize(R);
return R;
}
}
其他
有了分裂和合并,剩下的函数就很好实现了。
插入
新建的节点的权值的 v a l val val,我们将 ≤ v a l \le val ≤val 和 > v a l > val >val 的分裂,然后将新建的节点合并。
void insert(int val){
int L, R;
SplitVal(root, val, L, R);
root = merge(merge(L, newnode(val)), R);
}
这样我们需要调用一次分裂和两次合并,常数明显很大。
我们可以优化。
void insert(int val){
int u = root, z = newnode(val), f = 0;
for(;u && (d[u].rank < d[z].rank);f = u, u = (val < d[u].val ? d[u].ls : d[u].rs))++d[u].size;
if(f){
if(val < d[f].val)d[f].ls = z;
else d[f].rs = z;
}
else root = z;
SplitVal(u, val, d[z].ls, d[z].rs), getsize(z);
}
我们可以用循环寻找我们要插入的位置,然后把路径上的点的子树大小增加。
接着将这个位置原本的树按权值分裂成两棵,然后放在插入节点的两个儿子。
删除
我们将 < v a l , = v a l , > v a l < val,= val,> val <val,=val,>val 的部分分裂出来,最中间的那棵树就是要删除的。
由于只要删除一个数,我们将中间部分的左右儿子合并,然后将剩余的部分合并。
void del(int val){
int L, mid, R;
SplitVal(root, val, L, R);
SplitVal(L, val - 1, L, mid);
mid = merge(d[mid].ls, d[mid].rs);
root = merge(merge(L, mid), R);
}
我们用相似的方式进行优化。
因为题目保证删除的点存在(不保证就找到后再扫一遍),我们直接将路径上的子树大小修改。
然后将删除点的两个子树拼起来,放在删除点的原本位置。
void del(int val){
int u = root, f = 0;
for(;u && d[u].val != val;f = u, u = (val < d[u].val ? d[u].ls : d[u].rs))--d[u].size;
if(u){
u = merge(d[u].ls, d[u].rs);
if(f){
if(val < d[f].val)d[f].ls = u;
else d[f].rs = u;
}
else root = u;
}
}
查询部分
可以像开头 BST 的那样询问,也可以像这里借助分裂合并(常数较大)。
//我们将 <x 的分裂出,然后一直往右走,走到头就是前驱。
int pre_val(int x){
int L, R, now;
SplitVal(root, x - 1, L, R), now = L;
while(d[now].rs)now = d[now].rs;
return root = merge(L, R), d[now].val;
}
//类似
int next_val(int x){
int L, R, now;
SplitVal(root, x, L, R), now = R;
while(d[now].ls)now = d[now].ls;
return root = merge(L, R), d[now].val;
}
//将 <x 的分裂,答案就是这棵树的大小。
int query_rank(int val){
int L, R;
SplitVal(root, val - 1, L, R);
int ans = d[L].size + 1;
return root = merge(L, R), ans;
}
//用排名分裂,然后取子树的最大值。
int kth(int rak){
int L, R, now;
SplitRank(root, rak, L, R), now = L;
while(d[now].rs)now = d[now].rs;
return root = merge(L, R), d[now].val;
}
完整代码
序列操作
我们可以将树的中序遍历看做序列顺序的。
然后用按排名分裂,分成 [ 1 , l − 1 ] , [ l , r ] , [ r + 1 , n ] [1, l - 1], [l, r], [r + 1, n] [1,l−1],[l,r],[r+1,n] 三块。
给中间的块打上标记,之后在访问的时候 pushdown 即可。
可持久化
不知道什么是可持久化的看这:可持久化数据结构简介。
打上注释的是添加的操作。
void split(int now, int val, int&L, int&R){
if(!now)return void(L = R = 0);
int w;
if(d[now].val <= val){
d[L = newnode(1)] = d[now];//
split(d[now].rs, val, d[L].rs, R), getsize(L);
}
else {
d[R = newnode(1)] = d[now];//
split(d[now].ls, val, L, d[R].ls), getsize(R);
}
return getsize(L);
}
int merge(int L, int R){
if(!L || !R)return L + R;
int w;
if(d[L].rank < d[R].rank){
d[w = newnode(1)] = d[L];//
return d[w].rs = merge(d[w].rs, R), getsize(w), w;
}
else {
d[w = newnode(1)] = d[R];//
return d[w].ls = merge(L, d[w].ls), getsize(w), w;
}
}
记得用一个数组存一下每个版本的根。






















 2213
2213

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








