27 _ 递归树：如何借助树来求解递归算法的时间复杂度？

我们都知道，递归代码的时间复杂度分析起来很麻烦。有一个巧妙的方式是借助递归树来分析递归算法的时间复杂度。

递归树与时间复杂度分析

我们前面讲过，递归的思想就是，将大问题分解为小问题来求解，然后再将小问题分解为小小问题。这样一层一层地分解，直到问题的数据规模被分解得足够小，不用继续递归分解为止。

如果我们把这个一层一层的分解过程画成图，它其实就是一棵树。我们给这棵树起一个名字，叫作递归树。我这里画了一棵斐波那契数列的递归树，你可以看看。节点里的数字表示数据的规模，一个节点的求解可以分解为左右子节点两个问题的求解。

通过这个例子，你对递归树的样子应该有个感性的认识了，看起来并不复杂。现在，我们就来看，如何用递归树来求解时间复杂度。

归并排序算法你还记得吧？它的递归实现代码非常简洁。现在我们就借助归并排序来看看，如何用递归树，来分析递归代码的时间复杂度。

归并排序的原理我就不详细介绍了，如果你忘记了，可以回看一下第12节的内容。归并排序每次会将数据规模一分为二。我们把归并排序画成递归树，就是下面这个样子：

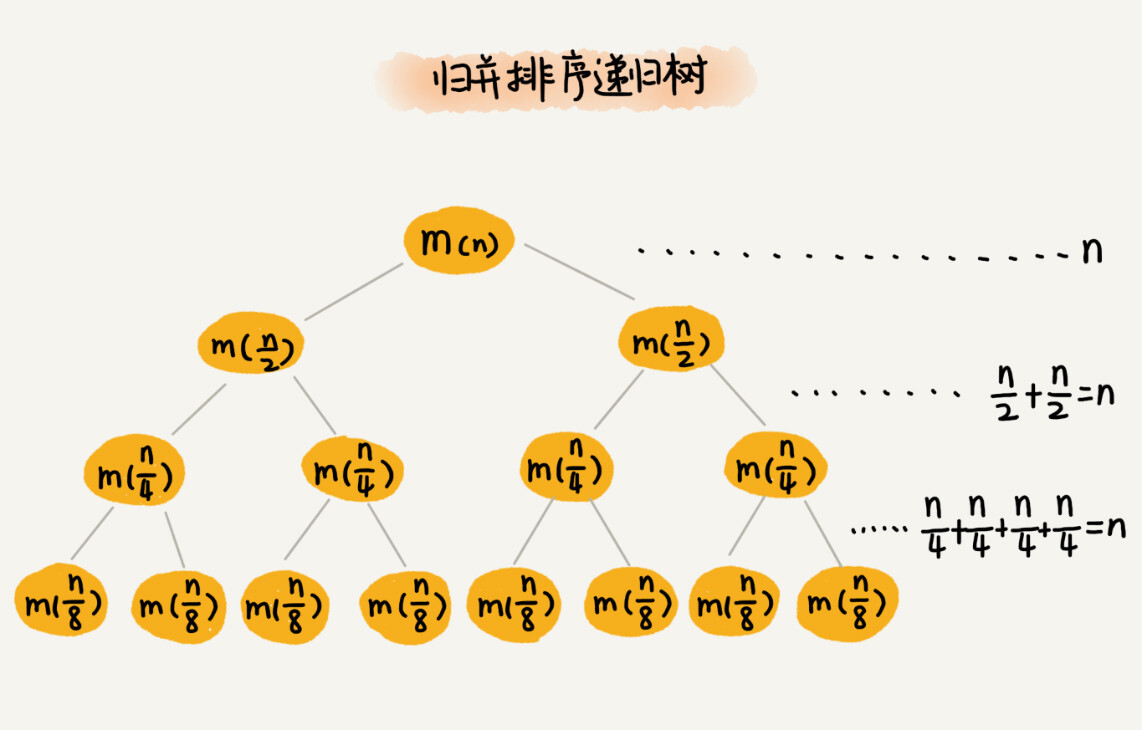
因为每次分解都是一分为二，所以代价很低，我们把时间上的消耗记作常量1。归并算法中比较耗时的是归并操作，也就是把两个子数组合并为大数组。从图中我们可以看出，每一层归并操作消耗的时间总和是一样的，跟要排序的数据规模有关。我们把每一层归并操作消耗的时间记作n。

现在，我们只需要知道这棵树的高度h，用高度h乘以每一层的时间消耗n，就可以得到总的时间复杂度O(n*h)。

从归并排序的原理和递归树，可以看出来，归并排序递归树是一棵满二叉树。我