poj 1177 & hdu 1828 Picture(线段树+离散化)

Picture

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1095    Accepted Submission(s): 608

Problem Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter. 

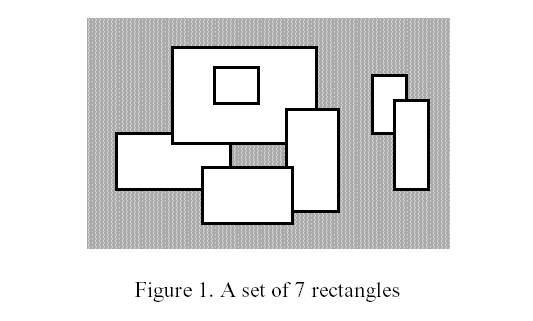
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1. 



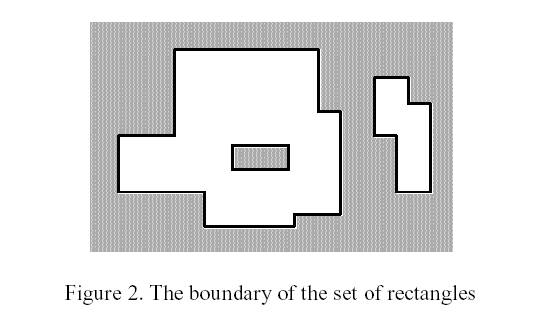
The corresponding boundary is the whole set of line segments drawn in Figure 2. 



The vertices of all rectangles have integer coordinates.

 

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate. 

0 <= number of rectangles < 5000 
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Please process to the end of file.

 

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

 

Sample Input

  

   7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16
  

 

Sample Output

  

   228
  

 

Source

IOI 1998

 

Recommend

linle

 

分析：这道题算是经典题吧，线段树+离散化。。。什么是离散化，囧，原来是那种东东，没什么好说的，开始时读入弄错了好像，

           居然没检查出来，还有，为什么坐标想同的每次都要分开计算，甚是不解~~~还有这样竟然没有0ms。。。跟暴力差不多

注意：题目数据貌似有错。。。

大家试一下这组

3

0 0 1 2

0 2 1 4

1 1 2 3

答案：12

ac的程序输出16.。。。

原来那个觉得是对的(就是加上这句 if(x[i].d!=x[i+1].d) )输出12.。。。

如果有错请指正。

 

这题实在是揪心，第三次更新啦。。。囧，发现陈宏的解题方法有漏洞，不能简单地用前后两测度想减来求值（+abs(lt[1].m-gk)）。。。

附上一组数据： 

 

13

0 0 1 1

0 1 1 4

0 4 1 6

1 0 2 1

1 1 2 4

1 4 2 6

2 0 3 2

2 2 3 3

2 5 3 6

3 1 4 4

3 5 5 6

4 0 5 2

4 2 5 5

 

答案：32 

如果你是按y轴排序来做的，自己转换一下坐标试试

 

 

好吧最后发现陈牛的思想是对的，但是论文里貌似没讲清楚坐标相同的处理要按先插入后删除，这样才能保持正确性，正确代码在最后~~~

贴下代码(有漏洞)：

#include <cstdio> #include <algorithm> #include <cmath> using namespace std; const int maxn=5001; const int maxtree=65556; struct tree { int l,r,t,g,m; bool a,b; }lt[maxtree]; struct data { int d,p; }x[maxn*2]; int y[maxn][2],c; bool flag[maxn]; void maketree(int v,int l,int r) { lt[v].l=l,lt[v].r=r,lt[v].t=lt[v].g=lt[v].m=lt[v].a=lt[v].b=0; if(l+1==r)return; int m=(l+r)>>1,now=v<<1; maketree(now,l,m); maketree(now+1,m,r); } void updata(int v) { if(lt[v].t)lt[v].g=lt[v].a=lt[v].b=1,lt[v].m=lt[v].r-lt[v].l; else if(lt[v].l+1==lt[v].r)lt[v].g=lt[v].a=lt[v].b=lt[v].m=0; else { int now=v<<1; lt[v].a=lt[now].a,lt[v].b=lt[now+1].b; lt[v].g=lt[now].g+lt[now+1].g-(lt[now].b<[now+1].a); lt[v].m=lt[now].m+lt[now+1].m; } } void ltwork(int v,int l,int r) { if(l<=lt[v].l&<[v].r<=r)lt[v].t+=c; else if(lt[v].l+1<lt[v].r) { int now=v<<1; if(l<lt[now].r)ltwork(now,l,r); if(r>lt[now].r)ltwork(now+1,l,r); } updata(v); } bool cmp(data a,data b){return a.d<b.d;} int main(int argc, char* argv[]) { //freopen("car.in","r",stdin); //freopen("car.out","w",stdout); int i,j,n,gk,ans; scanf("%d",&n); for(i=j=0;i<n;++i,j+=2) scanf("%d%d%d%d",&x[j].d,&y[i][0],&x[j+1].d,&y[i][1]),x[j].p=x[j+1].p=i; sort(x,x+j,cmp); maketree(1,-10000,10000); for(i=0;i<n;++i)flag[i]=1; for(i=ans=gk=0;i<j;++i) { if(c=flag[x[i].p])flag[x[i].p]=0;else c=-1; ltwork(1,y[x[i].p][0],y[x[i].p][1]); //if(x[i].d!=x[i+1].d)//这句不能加，相同坐标每次也要算，囧 ans+=(x[i+1].d-x[i].d)*lt[1].g*2+abs(lt[1].m-gk),gk=lt[1].m; } printf("%d/n",ans); return 0; } 

无数次修改。。。汗：

#include <cstdio> #include <algorithm> using namespace std; const int maxn=5001; const int maxtree=65556; struct tree { int l,r,t,g,m; bool a,b; }lt[maxtree]; struct data { int d,p; bool o; }x[maxn*2]; int y[maxn][2],c; inline int ab(int a){return a>0?a:-a;} void maketree(int v,int l,int r) { lt[v].l=l,lt[v].r=r,lt[v].t=lt[v].g=lt[v].m=lt[v].a=lt[v].b=0; if(l+1==r)return; int m=(l+r)>>1,now=v<<1; maketree(now,l,m); maketree(now+1,m,r); } void updata(int v) { if(lt[v].t)lt[v].g=lt[v].a=lt[v].b=1,lt[v].m=lt[v].r-lt[v].l; else if(lt[v].l+1==lt[v].r)lt[v].g=lt[v].a=lt[v].b=lt[v].m=0; else { int now=v<<1; lt[v].a=lt[now].a,lt[v].b=lt[now+1].b; lt[v].g=lt[now].g+lt[now+1].g-(lt[now].b<[now+1].a); lt[v].m=lt[now].m+lt[now+1].m; } } void ltwork(int v,int l,int r) { if(l<=lt[v].l&<[v].r<=r)lt[v].t+=c; else if(lt[v].l+1<lt[v].r) { int now=v<<1; if(l<lt[now].r)ltwork(now,l,r); if(r>lt[now].r)ltwork(now+1,l,r); } updata(v); } bool cmp(data a,data b){return (a.d<b.d||(a.d==b.d&&a.o<b.o));} int main(int argc, char* argv[]) { int i,j,n,gk,ans; //freopen("a.in","r",stdin); //freopen("a.out","w",stdout); scanf("%d",&n); for(i=j=0;i<n;++i,j+=2) scanf("%d%d%d%d",&x[j].d,&y[i][0],&x[j+1].d,&y[i][1]),x[j].p=x[j+1].p=i,x[j].o=0,x[j+1].o=1; sort(x,x+j,cmp); maketree(1,-10000,10000); for(i=ans=gk=0;i<j;++i) { if(!(c=x[i].o))c=-1; ltwork(1,y[x[i].p][0],y[x[i].p][1]); ans+=(x[i+1].d-x[i].d)*lt[1].g*2+ab(lt[1].m-gk),gk=lt[1].m; } printf("%d/n",ans); return 0; } 

 n久之后又回来做这题:

#include<cstdio>
#include<cmath>
#include<iostream>
#include<algorithm>
#define ls rt<<1
#define rs rt<<1|1
#define lson l,m,ls
#define rson m,r,rs
using namespace std;
const int mm=11111;
const int mn=mm<<2;
struct seg
{
    int x,y1,y2,v;
}g[mm];
int y[mm],t[mn],s[mn],a[mn],b[mn],sum[mn];
int val,L,R;
void build()
{
    for(int i=0;i<mn;++i)s[i]=a[i]=b[i]=sum[i]=t[i]=0;
}
void updata(int l,int r,int rt)
{
    if(L<=y[l]&&R>=y[r])t[rt]+=val;
    else
    {
        int m=(l+r)>>1;
        if(L<y[m])updata(lson);
        if(R>y[m])updata(rson);
    }
    if(t[rt])s[rt]=a[rt]=b[rt]=1,sum[rt]=y[r]-y[l];
    else if(l==r)s[rt]=a[rt]=b[rt]=sum[rt]=0;
    else
    {
        a[rt]=a[ls],b[rt]=b[rs];
        s[rt]=s[ls]+s[rs]-(b[ls]&a[rs]);
        sum[rt]=sum[ls]+sum[rs];
    }
}
bool cmp(seg a,seg b)
{
    return a.x<b.x||(a.x==b.x&&a.v>b.v);
}
int main()
{
    int i,j,n,m,tmp,ans;
    while(~scanf("%d",&n))
    {
        for(j=i=0;i<n;++i,j+=2)
        {
            scanf("%d%d%d%d",&g[j].x,&y[j],&g[j+1].x,&y[j+1]);
            g[j].y1=g[j+1].y1=y[j];
            g[j].y2=g[j+1].y2=y[j+1];
            g[j].v=1,g[j+1].v=-1;
        }
        sort(y,y+j);
        sort(g,g+j,cmp);
        for(m=i=0;i<j;++i)
            if(y[m]<y[i])y[++m]=y[i];
        build();
        for(ans=tmp=i=0;i<j;++i)
        {
            L=g[i].y1,R=g[i].y2,val=g[i].v;
            updata(0,m,1);
            ans+=(g[i+1].x-g[i].x)*s[1]*2+abs(sum[1]-tmp),tmp=sum[1];
        }
        printf("%d\n",ans);
    }
    return 0;
}