基于A*算法的公交最短路径

原创于 2025-10-12 01:46:27 发布 · 251 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#A*算法 #TRANSIT算法 #公共交通

在公共交通系统中寻找最短路径和换乘节点

妙图扎和敏敏欣*

摘要

向公共交通用户提供最重要的信息之一是用户指定的当前和目的地之间的最快公交路线。在本系统中，采用A*算法来查找仰光市中心区域的最短路径和公交路线信息。该系统不仅提供直达信息，还能提供当前公交站与目的公交站之间的换乘信息。公交路线、公交车信息、公交站及其相关位置、纬度/经度和道路名称均存储于空间数据库中。当用户需要查询公交路线信息时，首先输入当前位置和目的地，系统便从数据库中检索相关的公交路线。

获取公交路线后，使用A*算法计算最短路径。通过使用TRANSIT算法，换乘路线及信息将显示在地图上。本文采用仰光地区矢量地图作为底图。

关键词 A*算法 · TRANSIT算法 · 道路网络 · 公共交通系统

1 引言

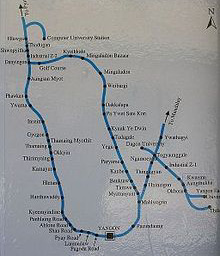
仰光地区的交通问题直接影响了该地区市民的生活质量。仰光地区的大多数市民使用公共交通工具，如公交车、出租车、铁路等。图1展示了仰光地区的一些公共交通类型。仰光地区交通带来的影响包括空气污染、噪音污染、路上浪费时间以及碳氢燃料的消耗。尽管道路数量在不断增加，仰光地区的交通问题仍然存在。先进的公共交通系统是智能交通系统的重要组成部分，有助于减少交通需求。我们报告了为游客提供公交车信息的算法，以鼓励人们使用公共交通系统。提供换乘信息是促进公共交通系统的另一种有效措施 [4]。

有许多算法可用于确定网络中两个节点之间的最短路径。其中，迪杰斯特拉算法和A*算法效率更高。迪杰斯特拉算法用于确定从源点到其他每个节点的最短路径，而A*算法与迪杰斯特拉算法类似，基于启发式策略[8]。

一个将居住和就业中心整合在一起的高效的公共交通系统，在促进技能、劳动力和知识在各市场内部及之间流动、提升生产力[6]方面发挥着重要作用。公共交通走廊已被证明能够形成活动中心，推动以公共交通为导向的发展，并通过提供便捷的公共交通接入，提升周边房产价值。

在一些在线地图服务中，用户可能见过卫星影像。当这些图像从卫星或飞机上拍摄时，它们只是普通的图像，类似于照片。但要在地图上显示这些图像，需要将其与地图坐标关联起来。这个过程称为地理配准。一旦图像与地图坐标关联，就可以叠加在街道地图之上。对于地理配准，一些用户可以使用GIS软件（如ArcGIS或QGIS）对未地理配准的图像或扫描地图进行地理配准，并将其加载到Oracle空间数据库[3]中。

本文的其余部分组织如下。第2节描述了基本代表性网络结构。第3节介绍了本系统所采用的方法A*算法及相关功能。第3节简要说明了系统概述和数据。第5节讨论了如何在仰光市中心区域对所提出的系统进行实验。最后，第6节总结了本文并描述了未来计划。

示意图0

寻找公共交通系统中的最短路径和换乘节点

2 道路网络

一个公共道路网络是连接两个节点的链路，图G={N,E,R}，其中N={1 ≤ i ≤ n}表示所有节点的集合，n为节点数量，起点和终点节点分别为O, D。E={1 ≤ e ≤ m}是有向链路的集合，m为链路数量；R={1 ≤ r ≤ u}表示公交路线集合，u为链路数量。在本文中，算法用于关联公交站和公交路线。我们使用距离作为本文中的成本。图(2)展示了示例道路网络。

由一些节点（公交站）组成，在本文中，这些节点和公交线路构成网络。将公共交通网络定义为图G，其中≤ i ≤ n}表示所有节点的集合，n为节点数量，起点和终点节点分别为O, D。E={1 ≤ e ≤ m}是有向链路的集合，m为链路数量；R={1 ≤ r ≤ u}表示公交路线集合，u为链路数量。在本文中，算法用于关联公交站和公交路线。我们使用距离作为本文中的成本。图(2)展示了示例道路网络。

示意图1

2.1 邻接矩阵

本文中，我们用邻接矩阵表示图G中的节点，并为每个节点赋予一个唯一编号。该编号的值表示从该节点出发的直达路径数量。例如，图3展示了后继节点集M的邻接矩阵T和距离。

给定一个由若干节点集合组成的加权图G，我们希望得到这样的距离表结果表示目标对应的列。

表示交通网络中各位置之间的连通性。我们将网络中的每个位置指定为邻接矩阵M中的一个单元格，若可以从位置i出行到位置j，则邻接矩阵Mi,j的对应元素被设为相应的值。以下示例说明了如何使用邻接矩阵来表示一个简单的道路网络。

表示街道网络的ph，一个由位于图[9]中的源点和目的地组成的问题实例。对于这些情况，我们知道所有源点到所有目的地的距离，M×N查询是一个距离矩阵。该矩阵的一个条目表示对应于当前行的源点到对应于当前列的目的地的距离。

T=
ێێۏ ێێۍ
0 1 1 1 0 0
0 0 0 0 1 0
0 0 0 1 0 0
0 0 0 0 1 1
0 0 0 0 0 1
0 0 1 0 0 0
ےۑۑ ۑۑې

0 1 1 1 ∞ ∞
∞ 0 ∞ ∞ 1 ∞
∞ ∞ 0 1 ∞ ∞
∞ ∞ ∞ 0 1 1
∞ ∞ ∞ ∞ 0 1
∞ ∞ 1 ∞ ∞ 0
ۑۑے ۑۑې

示意图2

3 系统方法论

3.1 A*算法

A*算法是一种图搜索算法，用于在已知区域内从给定的初始节点找到通往目标节点的路径。哈特和尼尔松提出的A*算法[5]将启发式方法融入搜索过程的概念形式化。该算法采用“启发式估计”h(n)，用以估计经过节点n的最佳路线，按照此启发式估计值的顺序访问节点，遵循最佳优先搜索[7]的方法。

A*算法通过构建一个“CLOSED列表”来记录已评估的区域，一个“OPEN列表”来记录与已评估区域相邻的区域，并计算从“起点”出发的已行进距离以及到“目标点”的估计距离。A*中用于评估距离的启发式方法是：

f(n) = g(n) + h(n) (1)

其中：
- g(n) 是从起始节点到任意节点n的路径成本，
- h(n) 是从任意节点n到目标节点的启发式估计成本

3.2 A*算法步骤

创建一个仅包含起始节点n0的搜索图G。将n0放入名为OPEN列表的列表中。
创建一个名为CLOSED列表的列表，初始为空。
如果OPEN为空，则以失败退出。
选择OPEN中的第一个节点，将其从OPEN中移除并放入CLOSED列表。称此节点为节点n。
如果节点n是目标节点，则通过沿指针从节点n0到节点nn在图G中追踪路径，成功退出，并得到解。（这些指针定义了搜索树，将在步骤7中建立。）
扩展节点n，生成其后继节点集M，其中不包含图G中已经是节点n祖先的节点。将M中的这些成员作为节点n在图G中的后继节点加入。
对于M中那些尚未在图G中（即不在OPEN或CLOSED列表中）的成员，为其建立指向节点n的指针，并将这些M的成员加入OPEN列表。对于M中已经位于OPEN或CLOSED列表中的每个成员m，如果迄今为止发现到达m的最佳路径经过节点n，则将其指针重定向至节点n。对于M中已经位于CLOSED列表中的每个成员，将其在图G中的所有后代节点的指针重新定向，使其沿迄今为止发现的最佳路径反向指向这些后代节点。
将OPEN列表按f(n)值递增顺序排列。
转至步骤3。

3.3 启发式函数

启发式搜索已广泛应用于确定性和概率性规划中。启发式函数可用于控制A*算法的行为。欧几里得距离是h(n)的一种常用方法。

Distance = sqrt(dx² + dy²) (2)

其中：
- x1 = 当前位置的x坐标
- x2 = 目标位置的x坐标
- y1 = 当前位置的y坐标
- y2 = 目标位置的y坐标
- dx = |x2 - x1|
- dy = |y2 - y1|

如果h(n)始终低于从节点n移动到目标的成本，则A*算法能够保证找到一条最短路径。如果h(n)恰好等于从节点n移动到目标的成本，那么A*算法将只沿着最优路径前进，而不会扩展其他任何节点，从而使其非常快速。如果h(n)有时大于从节点n移动到目标的成本，则A*算法无法保证找到最短路径，但可以运行得更快。在另一个极端情况下，如果h(n)相对于g(n)非常高，则只有h(n)起作用，A*算法就转变为最佳优先搜索。

3.4 换乘算法

换乘算法是用于在超大规模道路网络中寻找最短路径的方法之一。TRANSIT算法的一个优点是最终的查询时间完全不考虑起点的坐标节点，并考虑换乘次数和目的地[13],[14]。图4展示了公交路线中的一个示例。假设有三条公交线路B→C→D→E和G→D→E。乘客希望从某点出发，在B或D处可能需要换乘一条线路，可以在另一端换线。

示意图3

3.4.1 识别换乘节点的算法

for si Є VS
其中，Si,Sj = a H V E
((si,sj) Є E)，如果 (Sj ⊂ Si)，则 H := H \ sj；否则如果 (Si ⊂ Sj)，则 H := H \ si；否则 if (Si ≠ Sj)，则 H := H ∪ {si, sj}

一组公交线路 H = 换乘节点 V = 顶点 (公交车站) = 边 (公交线路连接)

4 系统概述

在本文中，公交区域（如公交车站位置）存储在空间数据库中，n为数量。仰光市中心的公共交通信息，包括名称、公交路线名称、公交车类型、纬度和经度的空间数据库。A*算法的时间复杂度与节点数量相关。该系统可在无互联网环境下使用。

连接。在图5中，显示了一些公交站和公交路线的数据。当用户在搜索框中输入地名（公交站名）时，地图会在相应位置显示一个标记。当用户输入源点和目的地公交站后，系统会从数据库中搜索可用的公交线路，然后在地图上显示公交线路。在图6中，展示了系统的流程图。将地名与地图上的坐标关联的过程称为地理编码。在空间数据库中，此类数据作为线图层存储，地名作为位置的属性。这是一种地理编码方式[11]。对于地址，其对应的坐标并不直接保存在数据库中，而是通过一种称为线性参考的方法计算得出。沿较长路段的起始和结束地址被保存下来，中间地址通过插值计算，进而求得坐标。

示意图4
示意图5

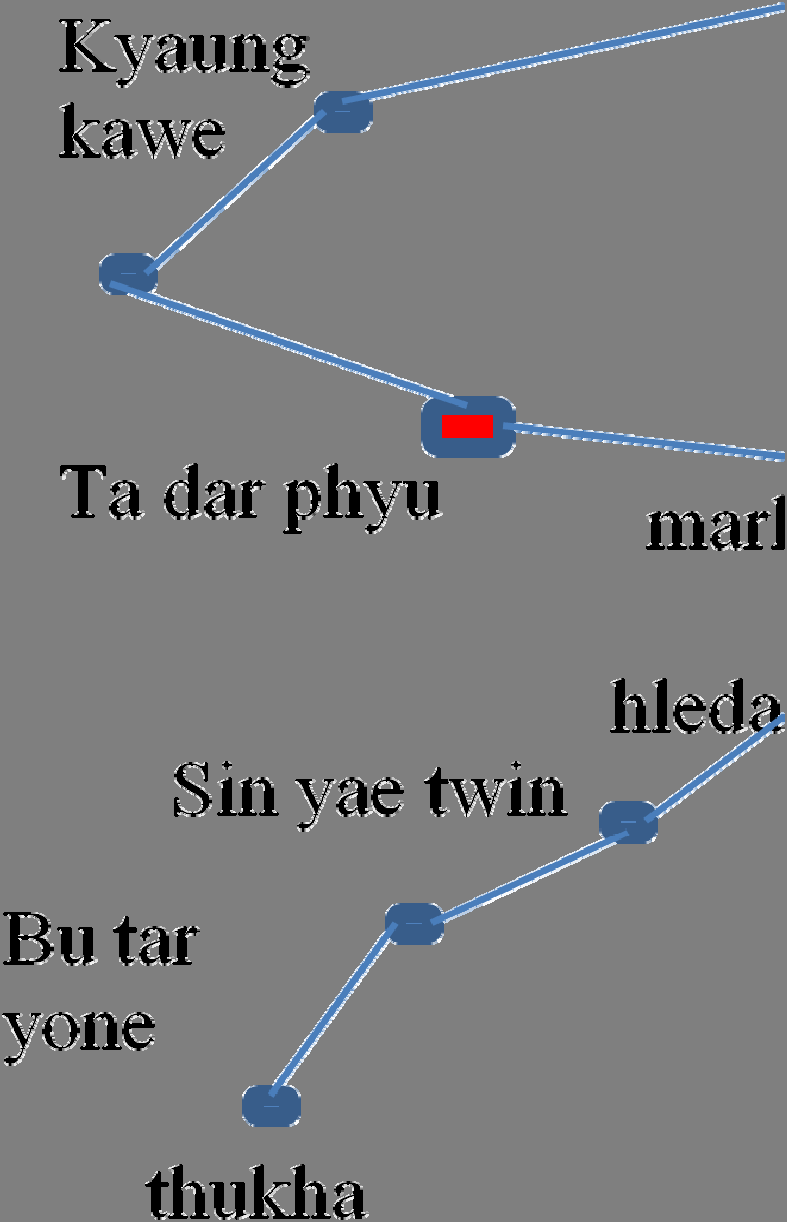
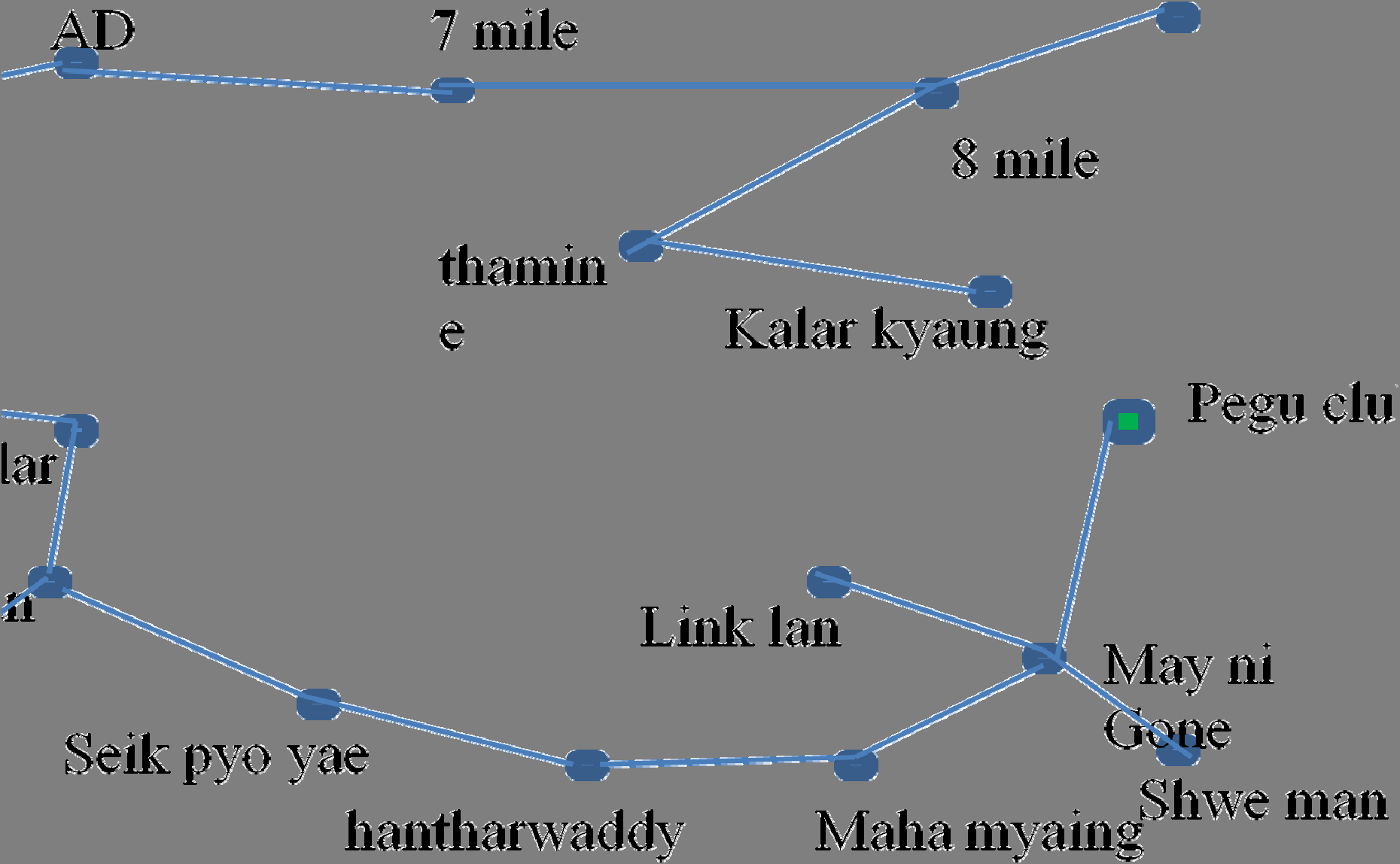
5 实验

本文中，所提出的系统在仰光市中心区域的道路网络上进行了测试。通过谷歌地球收集了仰光市中心地区的公交路线信息、公交站、道路名称及其相关的地理信息数据（如纬度/经度和位置），并使用GPS GARMIN etrex-10设备进行数据采集。仰光市中心区域的范围限定为左端纬度17·03‘56.63”N至右端经度96·19‘04.15”E。所采集的数据存储于空间数据库中，用于开发基于图论的A*算法以计算最短路径。该系统能够向用户展示数据，使其选择仰光市中心区域公共交通中的最优路线和公交编号。可利用TRANSIT算法计算公交路线中的换乘节点。图7展示了本系统的仰光区域矢量图。

示意图6