【洛谷 3353】在你窗外闪耀的星星

【题目】

传送门

题目描述：

飞逝的的时光不会模糊我对你的记忆。难以相信从我第一次见到你以来已经过去了 $3$ 年。我仍然还生动地记得，$3$ 年前，在美丽的集美中学，从我看到你微笑着走出教室，你将头向后仰，柔和的晚霞照耀着你玫瑰色的脸颊。我明白，我已经沉醉于你了。之后，经过几个月的观察和窥探，你的优雅与智慧，你对待生活的态度和你对未来的愿望深切地在我心中留下了印象。你是迷人的阳光女孩，我总是梦想着与你分享余生。唉，实际上你远远超过了我最疯狂的梦想。我不知道如何桥起我与你之间的鸿沟。所以我没有任何计划，仅仅只是等待，等待一个适当的机会到来。直到现在，毕业的到来，我意识到我是个傻瓜，我应该创造机会并且抓住它而不只是等待。

这些日子里，我和我的朋友、室友、同学一个接一个地分开。我仍无法相信，在挥手之后，这些熟悉的面孔很快就会从我们的生活中消失，仅仅留下回忆。我明天就将离开学校。你已经计划远走高飞，追求你的未来，实现你的梦想。如果没有命运，也许我们不会再次相遇。所以今晚，我正在你的宿舍楼下徘徊，希望能偶然遇见你。但矛盾的是，你的美貌一定会使我心跳加速，我笨拙的舌头也许无法吐出一个字。我不记得我曾多少次经过你的宿舍楼，每次都希望看到你出现在阳台上或是窗台上。我不记得这个想法曾多少次在我的脑海中涌出：打电话叫她一起吃晚饭或是聊聊天。但每次，考虑到你的优秀和我的平凡，胆怯的优势超越勇气驱使我静静地离开。

毕业，意味着中学生活的终结。这些光荣与浪漫的时代结束。你可爱的微笑是我原来努力学习的动力，这单相思的爱情会被密封，作为一个我心灵深处的记忆。毕业，也意味着新生活的开始，一个到达光明未来的足迹。我真希望你在国外天天开心，一切顺利。同时，我将努力从幼稚中走出来，变得更加成熟。我的理想将是在现实中追求我的爱与幸福，我永远不会放弃。

再见了，我的公主！

如果有一天，在某个天涯海角，我们有机会相聚，即使是白发苍苍的男人和女人，在那个时候，我希望我们可以成为好朋友来自豪地分享这个记忆，重温年轻快乐的激情。如果这个机会永远没有到来，我希望我是天空中的星星，在你的窗外闪烁。远远地保佑着你，就像一个朋友，每天晚上陪伴在你左右，一同分享甜美的梦亦或是一同经历可怕的梦。

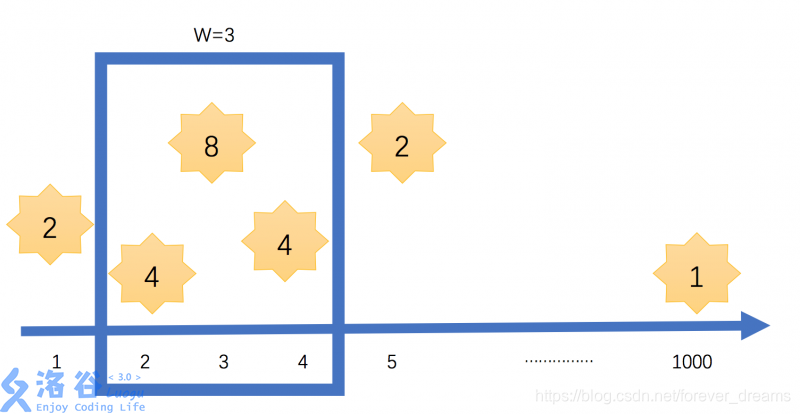
现在问题来了：天空可以理解为一条数轴，在这条数轴上分布着许多颗星星，对于每颗星星都有它的位置 $x_i$ 和自身的亮度 $b_i$。而窗户所能看到的范围是一个给出的参数 $w$，我们看到的星星也包括窗户边缘的星星。现在，要你求出调整窗户位置后能看到星星的亮度之和最大值。

输入格式：

一行 $n,w$，分别代表星星的数量和窗户的宽度

余下 $n$ 行，输入 $x_i$ 和 $b_i$，代表星星的坐标和亮度

输出格式：

一个数字，代表能看到星星的最大亮度和

样例数据：

输入
6 3
1 2
2 4
3 8
4 4
5 2
1000 1

输出
16

说明：

【样例说明】

【数据范围】

对于 $10\%$ 的数据，$w=0$（没有边缘）
对于 $40\%$ 的数据，$w\le 1000$
对于 $100\%$ 的数据，$n\le 100000$，$w\le 100000$，$x_i\le 100000$，$1\le b_i\le 100$
除 $w=0$ 的情况外，$w$ 均为 $\ge 3$ 的奇数

【分析】

我会告诉你这是一道水题吗

这道题先是标题吸引了我，然后是题目描述吸引了我，然后我就写了。。。

其实只用记录一下每个点的前缀和，然后从前往后扫一遍就行了

【代码】

#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 100005
using namespace std;
int x[N],sum[N];
int main()
{
	int n,w,i,pos,val;
	scanf("%d%d",&n,&w);
	for(i=1;i<=n;++i)
	{
		scanf("%d%d",&pos,&val);
		x[pos]+=val;
	}
	int ans=0;
	for(i=1;i<N;++i)  sum[i]=sum[i-1]+x[i];
	for(i=w;i<N;++i)  ans=max(ans,sum[i]-sum[i-w]);
	printf("%d",ans);
	return 0;
}