格密码LLL算法：如何解决最短向量SVP问题（1）

原创已于 2024-01-12 23:58:21 修改 · 7.4k 阅读

48 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #密码学 #网络安全

于 2022-03-26 22:36:12 首次发布

格密码专栏收录该内容

46 篇文章

订阅专栏

本文介绍LLL算法及其在解决最短向量问题(SVP)中的应用,包括分解多项式、多项式解的求解及整数关系的确定等。同时也探讨了格基约化的概念和技术。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

最短向量问题：Shortest vector problem，SVP。本文章将分析一个解决最短向量（SVP）问题的算法。

在1982年，A.K.Lenstra，H.W.Lenstra,Jr和L.lovasz提出一种解决SVP问题的算法，取三个人的名字首字母，所以通常称之为LLL算法。当然因为SVP是NP-困难问题，所以不能完全解决，只能近似解决。近似因子（approximation ratio）为:

$(\frac{2}{\sqrt 3})^n$

在1801年，Gauss曾给出一个解决二维空间SVP问题算法。某种意义上，LLL算法可以看成解决多维空间SVP问题的算法。

在1987年，Schnorr改进过LLL算法，将解决的近似因子改进到：

$2^{O(\frac{n(loglogn)^2}{logn})}$

一. LLL算法的应用

LLL算法最早可作为网络安全的分析工具，具体的应用包括：

1. 在整数和有理数的范畴内，分解多项式。

2. 找到多项式方程足够精确的代数解。

3. 确定整数线性关系。给定实数集合 $\lbrace x_1,\ldots,x_n\rbrace$ ，如果能找到一个整数集合 $\lbrace a_1,\ldots,a_n\rbrace$ ，使得：

$a_1x_1+\ldots+a_nx_n=0$

其中 $a_i$ 不全为0（全为0则是平凡解），则称此实数集合满足整数关系。

4. 整数规划（interger programming）。整数规划问题属于典型的NP完全类问题，对于有限变量个数的整数规划问题，LLL算法可以在多项式时间内输出优解。

5. 可近似解决格的另一个基本问题：最近向量问题（Closesr Vector Problem, CVP)。

6. 在密码分析中应用广泛，例如攻击密码协议。LLL算法可以攻击基于背包向量（knapsack）的密码系统，以及攻击基于低公共指数的RSA公钥密码方案。

例1：分解多项式

如将 $x^2-1$ 分解成 $x+1$ 和 $x-1$ 。

例2：多项式的解

如 $x^2-2=0$ 的输出近似解为1.414213

$x^2+4x-3=0$ 的输出近似解为0.645751

例3：整数关系

如，给出如下三个数：

$arctan(1)\approx0.785398\\ arctan(\frac{1}{5})\approx0.197395\\ arctan(\frac{1}{239})\approx 0.004184$

请寻找它们的整数关系。

解：

经过LLL算法可输出：

$arctan(1)-4arctan(\frac{1}{5})+arctan(\frac{1}{239})=0$

也就是第一个数的一倍，第二个数的4倍，第三个数的1倍，此时相加则为0.以上等式又被称为Machin 公式。

为了方便分析，后续统一讨论在满秩格以及 $l_2$ 范数下的LLL算法。讨论非满秩格以及其他范数也是类似的，可以直接推广。

为了全方位了解LLL算法，可以分为以下三个部分：

1. 定义LLL约化基；

2. 如何利用LLL约化算法寻找一个好基；

3. 分析算法的运行时间；

系列文章：

格密码LLL算法：如何解决最短向量SVP问题（2）_lll算法复杂度-优快云博客

格密码LLL算法：如何解决最短向量SVP问题（3）（完结篇）-优快云博客

二. 格基约化

在求解SVP问题时，最先想到的就是对格基的多种线性组合尝试。格密码中希望获得比较短的格基，所以算法最难的部分就是让两个坐标同时变小，如下图：

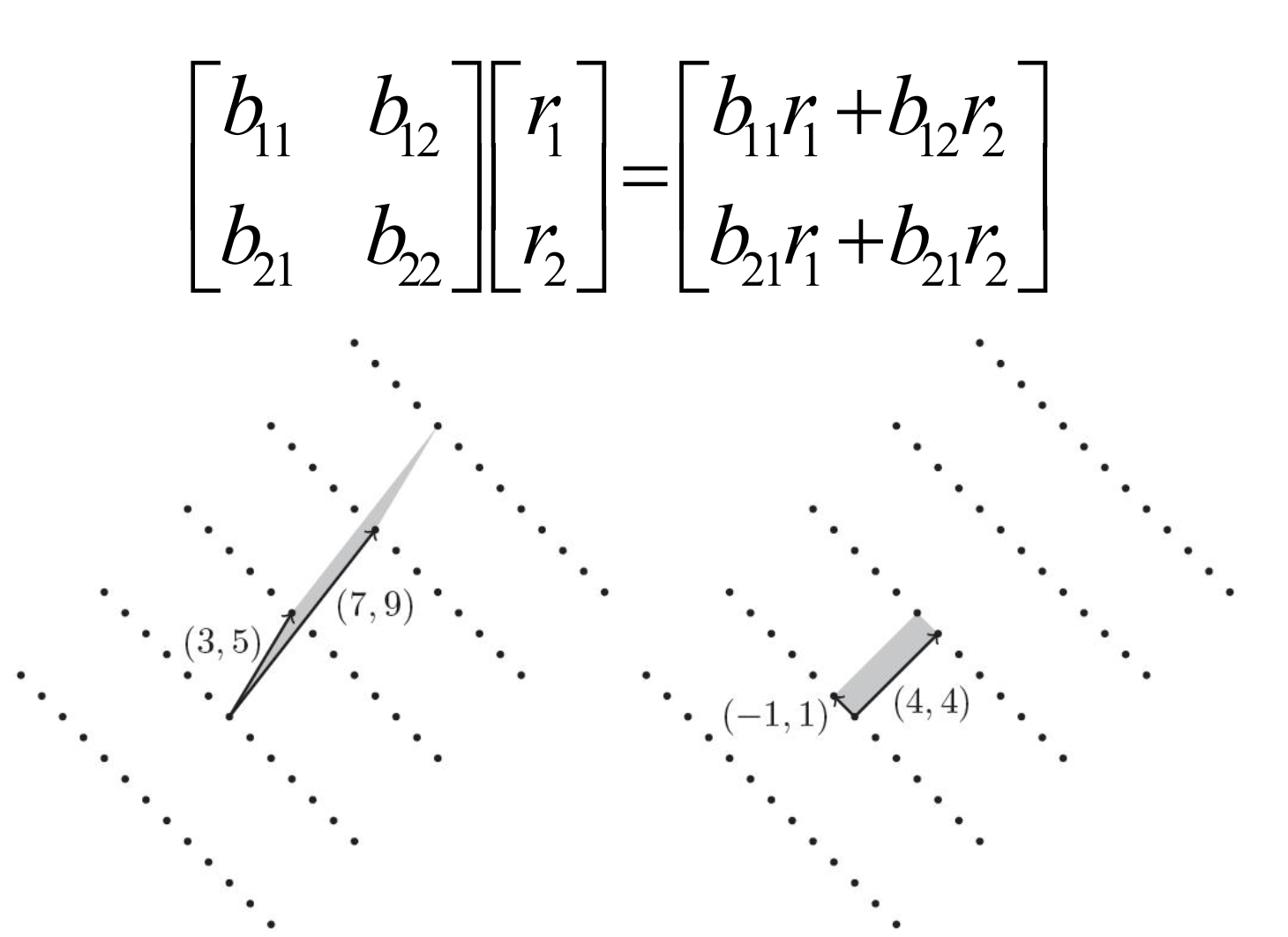
首先需要Gram-Schmidt正交化知识的铺垫。

定义1

给定n个线性独立的向量 $b_1,\ldots,b_n\in R^n$ ，对 $b_1,\ldots,b_n$ 的Gram-Schmidt正交化过程定义为：

$\tilde b_i=b_i-\sum_{j=1}^{i-1}\mu_{i,j}\tilde b_j$ $\mu_{i,j}=\frac{\langle b_i,\tilde b_j\rangle}{\langle\tilde b_j,\tilde b_j\rangle}$

此过程可以利用投影向量直接理解，注意以上过程得到的向量还没有归一化处理，也就是长度变为1.

Gram-Schmidt正交向量不改变格基本区的面积，而且当基向量比较接近时长度最短，如下图：

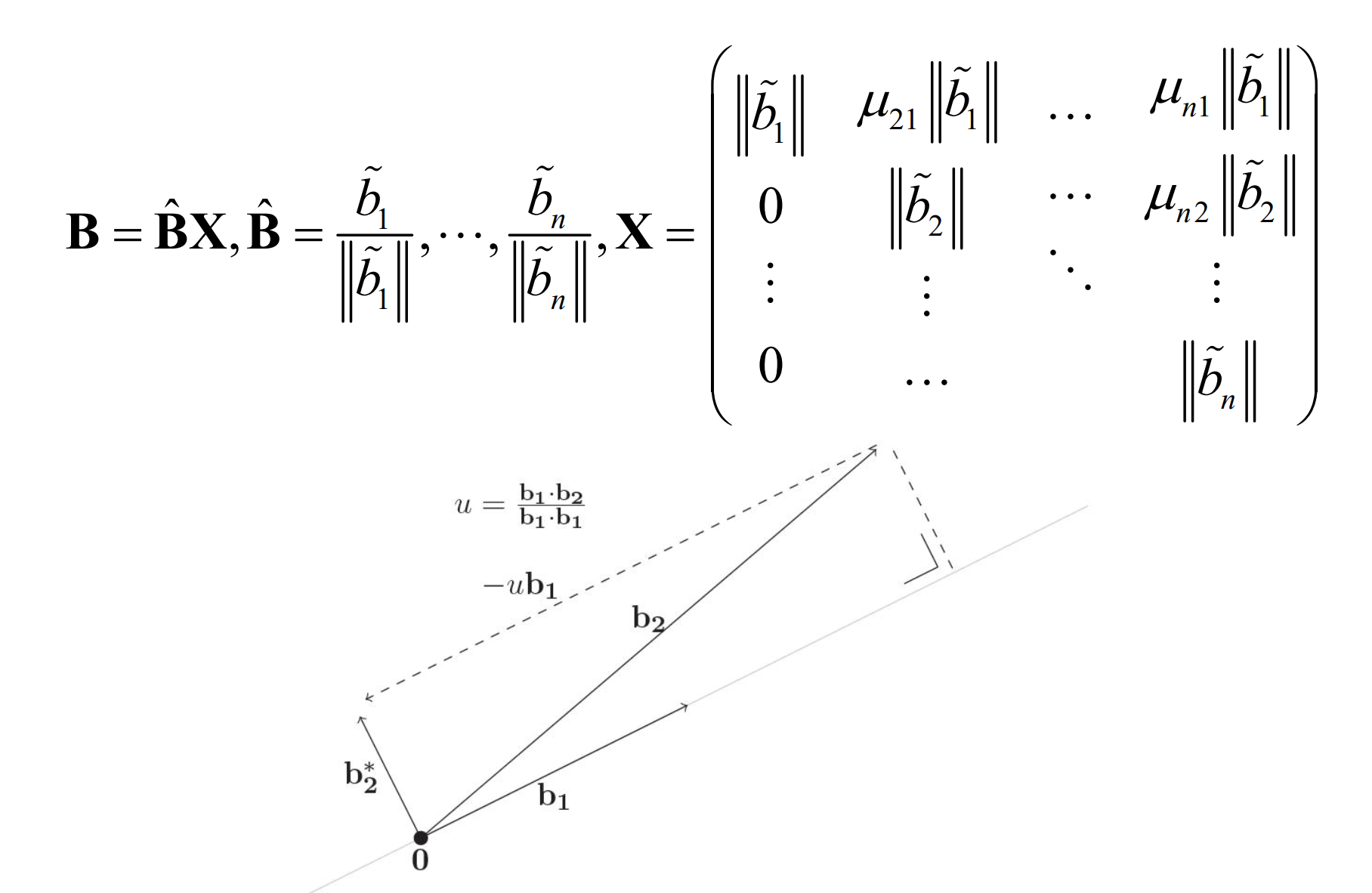
定义2

$\delta-LLL$ 格基约化需满足如下两个条件：

$\forall 1\leq i\leq n, j<i\quad \lvert\mu_{i,j}\rvert\leq\frac{1}{2}$
$\forall 1\leq i<n.\quad \delta\lVert\tilde b_i\rVert^2\leq\lVert\mu_{i+1,i}\tilde b_i+\tilde b_{i+1}\rVert^2$

LLL算法最终输出的基称为LLL约化基。

格基约化性质（1） LLL算法总能实现格基约化。

格基约化性质（2） $\delta=\frac{3}{4}$ 是该算法的一个特例，LLL算法成立的前提条件是：

$\frac{1}{4}<\delta<1$

格基约化性质（3）

根据LLL约化基的定义可得：

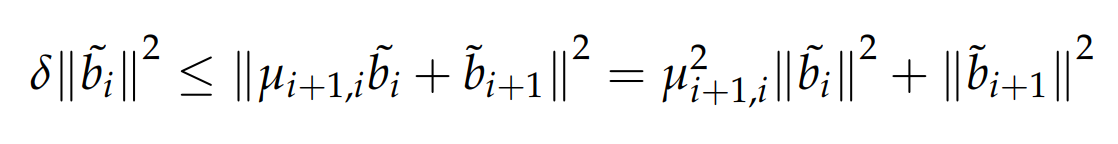
第一个不等号：LLL约化基的性质；

第二个等号：正交化后的向量两两垂直，相乘后结果为0

由于 $\tilde b_i$ 与 $\tilde b_{i+1}$ 相互垂直，可得：

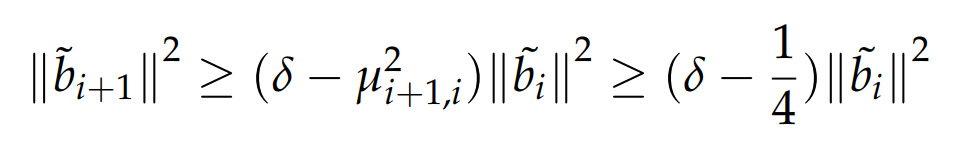
第一个不等号：移项可得；

第二个不等号：LLL约化基的第一个性质；

根据 $\delta$ 的范围，由此可得 $\tilde b_{i+1}$ 比 $\tilde b_i$ 短，但又不会短太多。

格基B在经过标准正交化处理后，可以看成如下：

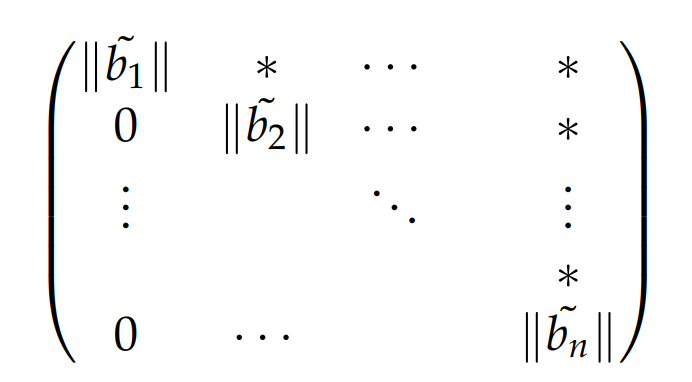
理解：该格基与原始格基B所形成的格是一样的，打星号的地方可看上面。此格基矩阵为上三角矩阵。

LLL约化基的定义保证了上三角的值不到同行对角线值的一半，由此可将上述矩阵改为：

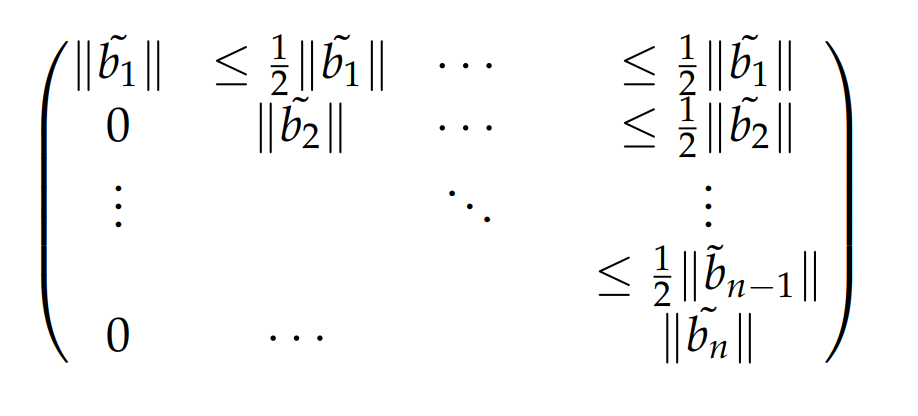
从相邻基向量的长度关系推导，从上面的矩阵中选取一个子矩阵，以 $2\times 2$ 矩阵为例，可得如下：

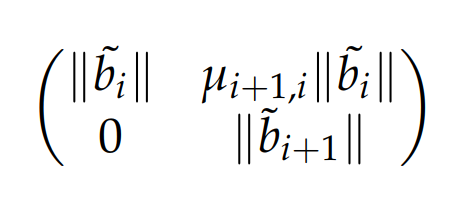
Schnorr算法对原始的LLL算法做了一些改进，其中最主要的改进就是在此矩阵的基础上。类推到 $k\times k$ 子矩阵（k>2)。

总结

格在密码分析领域中有着十分重要的地位.1996年，Coppersmith以多项式方程求小值解的问题为桥梁，把攻击RSA密码体制的问题转换为求格中短向量的问题，开辟了基于格的RSA密码分析的研究，他的工作也在后人的简化完善下逐渐形成了Coppersmith方法.

一方面，关于基于格的Coppersmith方法，包括模多项式方程求小值解的方法、整系数多项式方程求小值解的方法、求解近似公共因子问题的方法，还包括除Coppersmith 方法外的一种在低维格中寻找最短非零向量的格方法。另一方面，关于 RSA 密码分析，包括小加密指数攻击、小解密指数攻击、部分私钥泄露攻击、求解私钥d 与分解模数N 的等价性证明、隐式分解问题的分析、素因子部分比特泄露攻击、共模攻击等。

格密码作为抗量子密码的候选算法之一，在欧美布局已久，成果丰富，国内起步较晚，目前缺乏对本领域的创新性贡献。2012年美国NIST立项后量子密码标准项目，计划2024年推出产业标准；

2015年欧盟地平线科技2020计划抗量子旗舰项目，整合欧盟力量参与NIST标准竞选；

欧盟联合组队，在国际抗量子密码算法竞赛中遥遥领先。