LLL格基归约算法

格的介绍

首先要介绍一下什么是格，首先来看一个二位的坐标系，对于坐标席上一点(x，y)

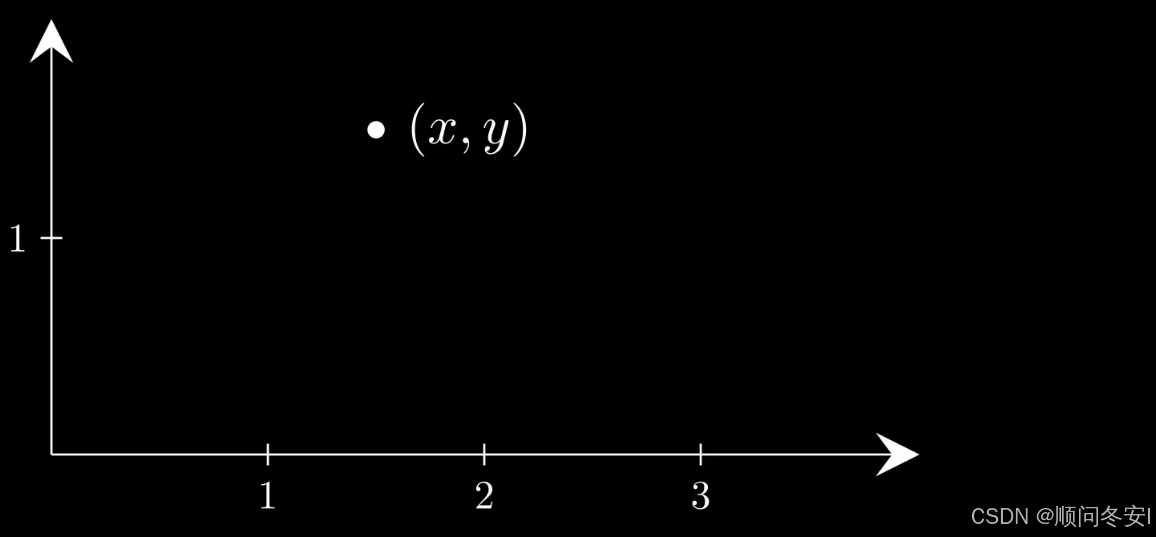
可以看作是两个基向量(1,0)和(0,1)的线性组合

线性组合的系数分别是x和y，假如限定这个系数是整数，那么得到的点x，y坐标都为整数

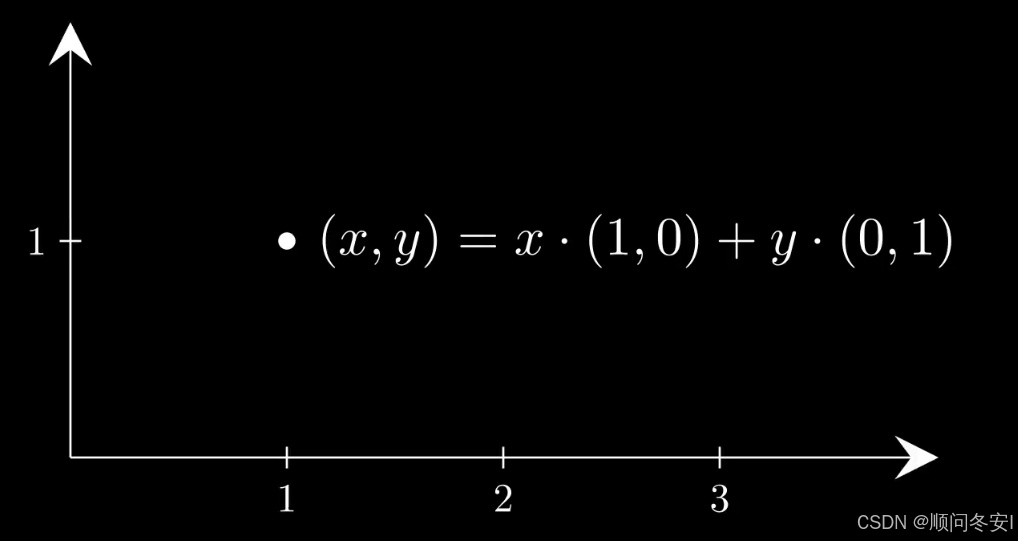
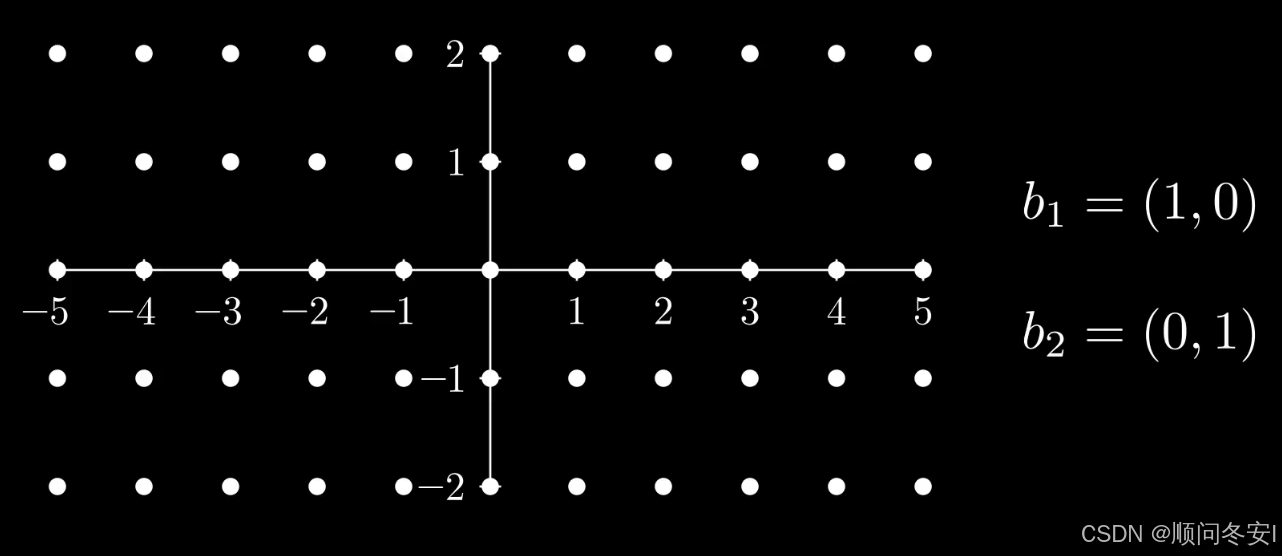
所有格点组成的集合，就成为格，我们称他为格点，因为所有的格点组成一个个字图案

如果换成信的一组基(2,0)和(0,1),得到得格中每一个点得x坐标都是偶数

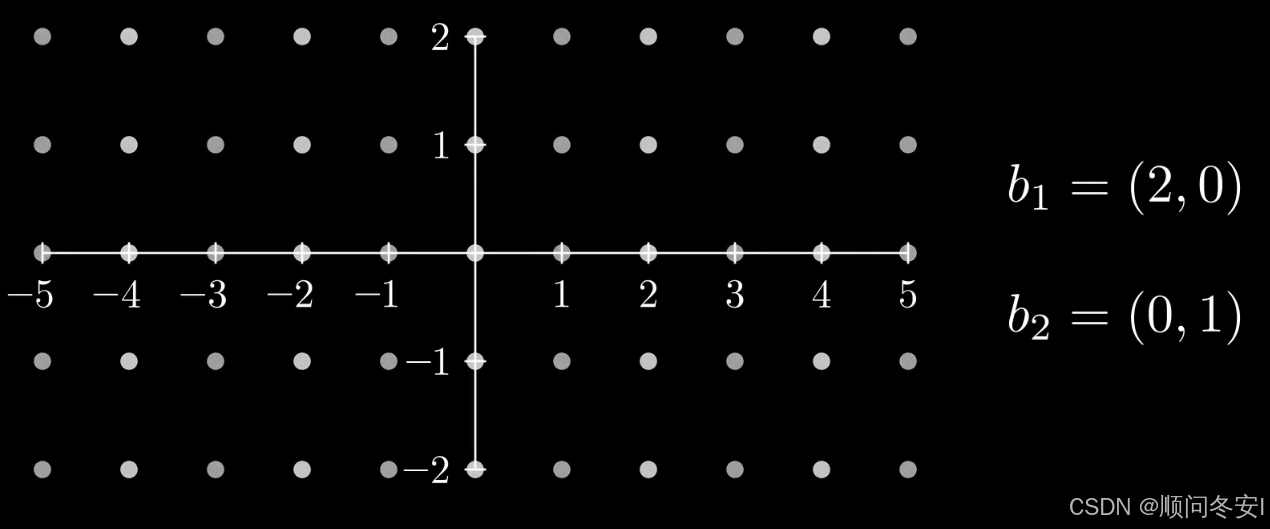
再举一个例子

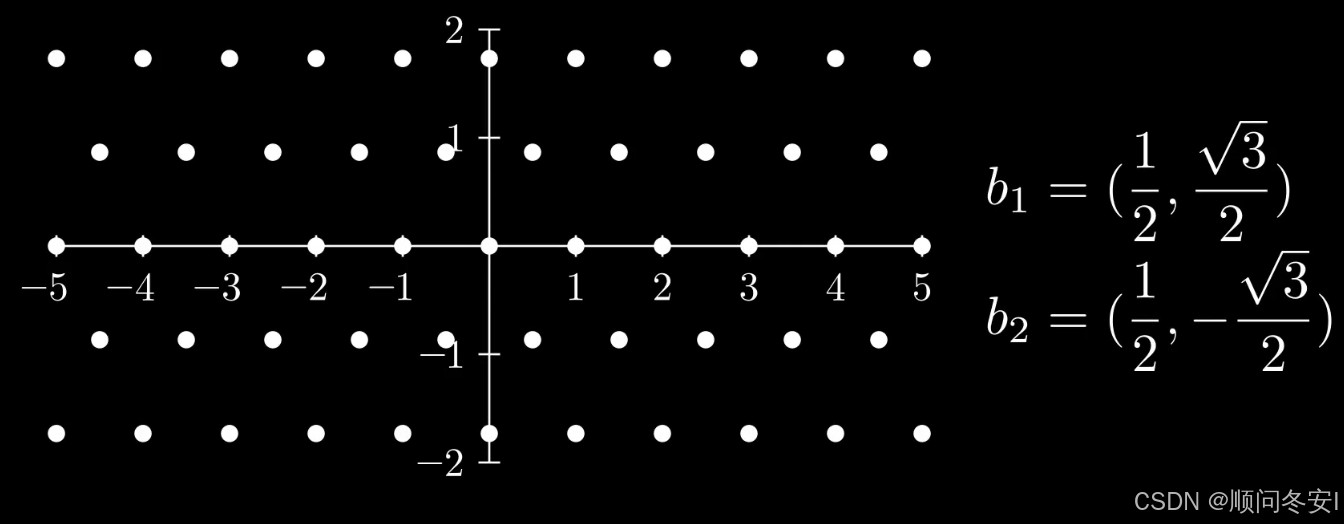
此时基向量不再和坐标轴平行，那么使用不同得基，会得到相同得格吗？

答案是肯定得，例如把第二个基向量改成(1,0)结果不变

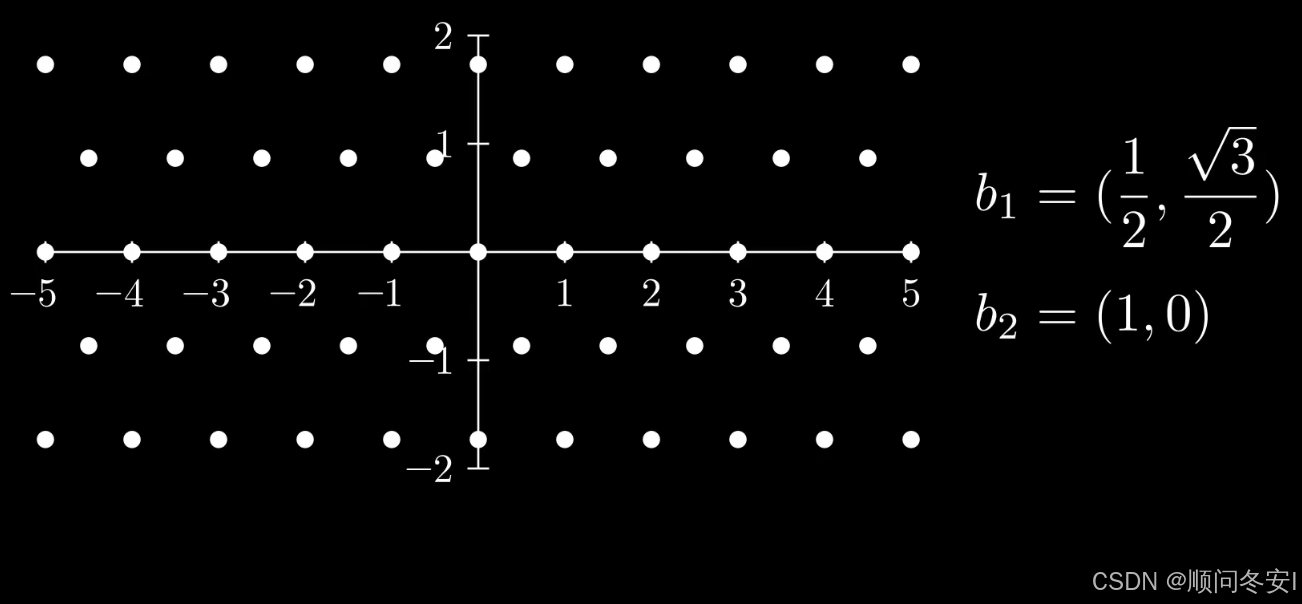
换一句话说，同一个格，可以用不同得基向量组来生成

定义

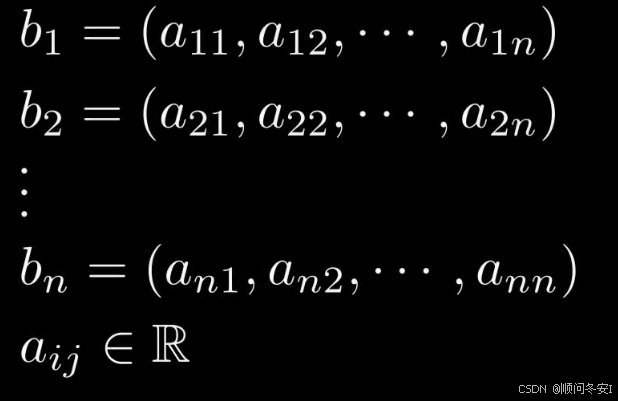
给定R^n空间中得n格基向量b_1到b_n那么格L就是基向量以整数位系数得线性组合得到的点的集合

格基的规约

前面已经提到，同一个格可以由不同的基向量组生成，例如L可以由b_1到b_n的基向量组生成，也可以由b_1'到b_n'的基向量组生成

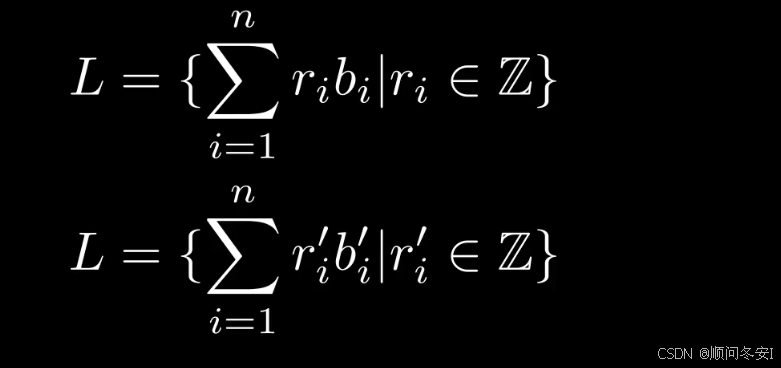
格基归约算法实现的是给定一组基向量，得到一组新的更好的基向量，那么问题出来了，什么是更好的基向量呢？

LLL格基归约算法算法保证了，归约后得到的第一个基向量b_1的大小是有界的，直观理解，就是得到的心想两的模场比较小

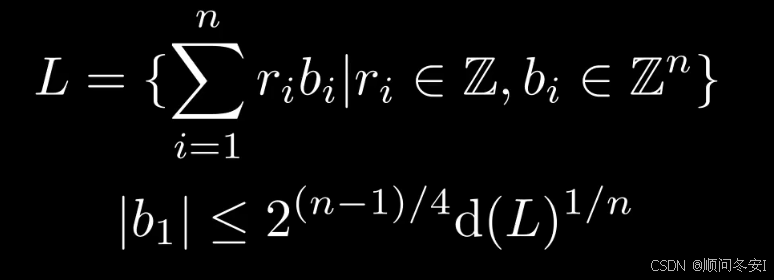
另外需要注意的是，LLL算法要求基向量在Z^n空间中

LLL算法应用场景

已知r是一个位置系数的整系数二次多项式的根，求整系数a、b、c

这个问题可以用LLL来解决，首先构造一组基b_1、b_2、b_3

我们希望这三个基向量在线性组合后，得到一个向量b_1'

此时b_1'的前三项系数就是所求的a、b、c

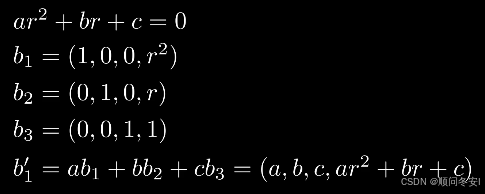
所以如果能求出b_1'，就能求出答案了

现在用LLL算法求b_1'

LLL算法保证了求出的第一个基向量的模长会比较小如果我们给它上一点压力，让某一项系数特别大

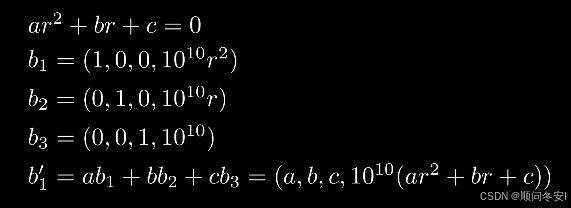
此时b_1'的模场主要取决于

的值了

相当于让LLL算法找到一组a、b、c使得

尽量小

而已知存在a、b、c使得

这样就达成了我们的目的，需要注意的是，由于LLL要求基向量属于Z^n空间，实际上这里还有一个取整操作

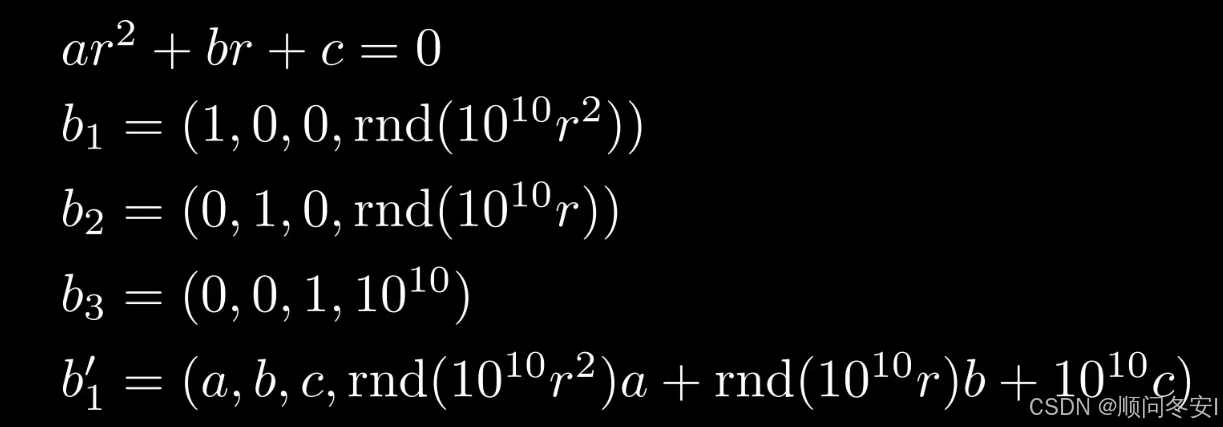
用类似的方法可以求解很多其他问题，例如针对RSA的Coppersmith攻击系列