SiamFC

Paper : Fully-Convolutional Siamese Networks for Object Tracking
Code : official

摘要

尽管之前有论文尝试将深度卷积神经网络应用到Object tracking 的任务中，但是由于实时性的要求，以及训练数据集的数据存在稀缺性，效果并不是很好。作者针对实时性的限制，提出使用全卷积神经网络进行特征提取，并使用孪生神经网络进行训练，并在ILSVRC15的数据集上进行训练，在VOT ALOV OTB数据集上进行测试。本文主要的贡献点有以下两个

• 全卷积神经网络+孪生神经网络在Object tracking中以远远超过帧速率要求的速度实现了非常有竞争力的性能。我们训练了一个孪生网络用来在较大的搜索图像中定位示例图像。
• 相对于搜索图像使用全卷积神经网络，可以通过计算其两个输入的互相关性的双线性层实现了密集而有效的滑动窗口评估。

网络结构

使用相似度学习的方法来解决Object tracking 任务，形式化的表述如下：学习一个函数 $f(z,x)$ ，该函数将示例图像 $z$ 与相同大小的候选图像 $x$ 进行比较，如果两个图像描述了相同的对象，则返回高分，否则返回低分。我们可以穷尽地测试下一帧中物体所有可能的位置，并选择与该对象的过去外观具有最大相似度的候选对象。

孪生神经网络形式化的表述为：孪生网络将一对输入使用相同的映射 $\phi$ 进行嵌入，使用距离函数 $g$ 描述嵌入向量之间的距离，最终函数 $f(z,x)=g(\phi (z),\phi (x))$。

使用全卷积网络的优势在于，我们可以提供更大的搜索图像作为网络输入，而不是使用相同大小的候选图像，它将一次计算在搜索图像中所有候选窗口。

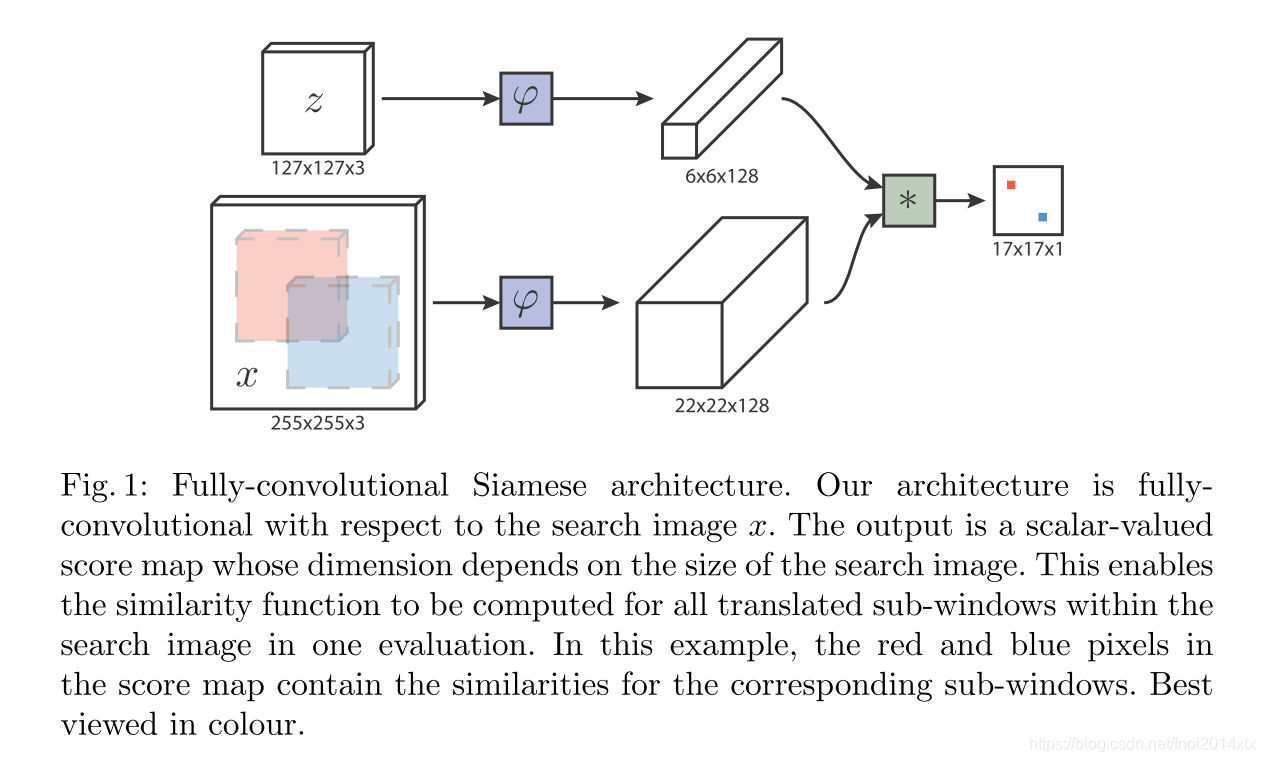
通过使用feature map的互相关来衡量示例图像与搜索图像的每个候选位置的相关性，互相关层定义如下

$$f(z,x)=\phi (z)\ast \phi (x)+b$$

其中，$b$ 为一个常数，表示将分数图中每个位置增大 $b$，互相关(Cross-correlation) 对于一维连续信号来说定义如下

$$(f\ast g)(\tau )={\int }_{-\infty }^{+\infty }{f}^{\ast }(t)g(t+\tau )dt$$

其中，$f^{\ast }$ 表示共轭，对于一维离散信号定义如下

$$(f\ast g)[n]=\sum _{-\infty }^{+\infty }{f}^{\ast }[m]g[m+n]$$

二维互相关运算具有相近的结构，互相关的最大优势在于可以使用FFT和IFT加速互相关运算的计算速度，即

$$\mathfrak{F}(f\ast g)=\mathfrak{F}(f{)}^{\ast }\odot \mathfrak{F}(g)$$

训练

对于示例图像和候选框，损失函数定义如下

$$l(y,v)=\log (1+\exp (-yv))$$

其中， y ∈ { + 1 , − 1 } y\in\{+1,-1\} y∈{+1,−1} 表示 ground-truth label，$v$ 为孪生网络对于该候选框位置的输出。

对于示例图像和整张搜索图像，损失函数为

$$L(\text{y},\text{v})=\frac{1}{|D|}\sum _{u\in D}l(\text{y}[u],\text{v}[u])$$

训练使用的数据对通过将示例图像和搜索图像同时通过padding的方式将物体定位框变换到图像正中央，如下图所示

对feature map 进行互相关运算之后得到的score map，ground truth 标记为

$$y[u]=\{\begin{array}{cc}+1& k||u-c||\le R\\ -1& \text{otherwise}\end{array}$$

其中，$k$ 表示全卷积网络中的总步长变化，$c$ 表示score map的中心点位置，$R$ 为超参数，表示在原图像中半径为 $R$ 的圆内标记为相同。

在训练过程中，使用127*127的样例图像，在255*255大小的搜索图像上操作。图像被缩放到bounding box + margin 与样例图像大小相同。假设bounding box 的尺寸为 $(w,h)$，margin宽度为 $p$，那么缩放系数 $s$ 满足

$$s(w+2p)s(h+2p)=A=127^2$$

取 $p=\frac{w+h}{4}$

CNN的网络结构如下，特别注意的是卷积还是池化层都不引入padding参数

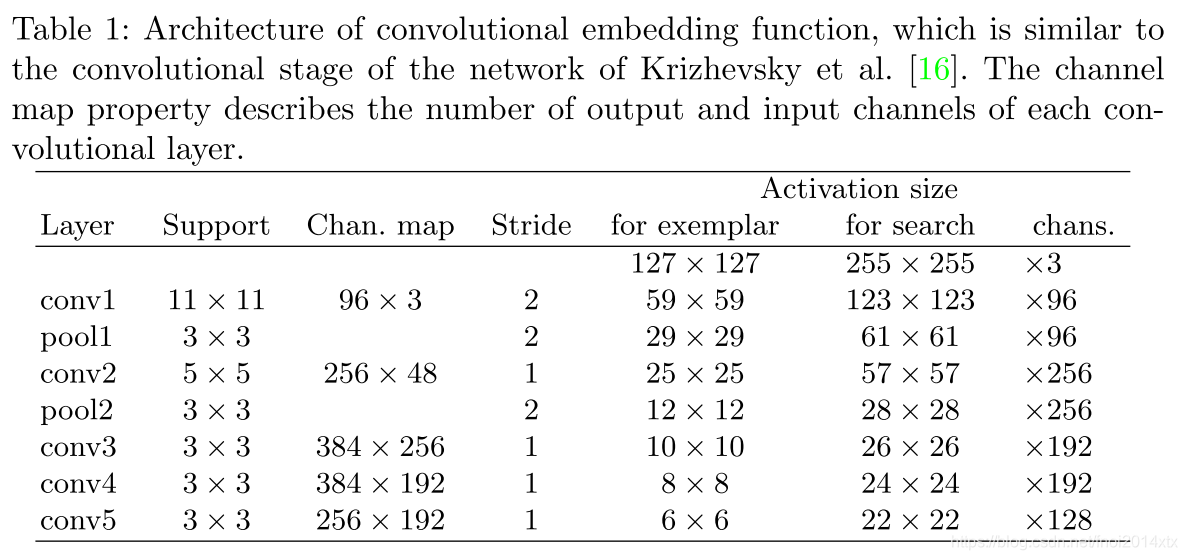
测试

在测试时，我们仅在示例图像对应的定位框四倍大小的区域内搜索对象，并将余弦窗口添加到得分图中以惩罚较大的位移结果。 通过处理搜索图像的多个缩放版本来实现缩放空间跟踪。比例尺的任何变化都会受到处罚，更新当前比例尺会受到阻碍。

在实现时，对score map 使用bicubic插值，放大到272*272，可以得到更精确的定位结果。

总结

根据feature map 保留了良好的空间信息的特性，将feature map 和原始图片之间的区域进行一一对应的方法，在Fast R-CNN中已经被使用过一次了，很难说这篇文章有没有参考Fast R-CNN，在这篇文章中，孪生神经网络不是重点，FCN应用到Object tracking并进行穷尽比对才是。