视觉SLAM理论入门——（3）李群与李代数

群的概念

群是一种集合加上一种运算的代数结构，若记集合为，运算为，则群记为。群满足以下性质（封结幺逆）：

1、封闭性

2、结合律

3、幺元

4、逆

 

李群与李代数

定义

李群是指具有连续光滑性质的群，整数群是离散的群，不是李群。前面说的特殊正交群和特殊欧氏群都属于李群（一个刚体可在空间中连续光滑旋转、平移）。

这两个李群对加法不封闭，但是对乘法封闭（两个旋转矩阵相乘表示做了两次旋转）：

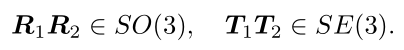
每个李群都有与之对应的李代数，李代数描述了李群的局部性质，定义如下：

李代数由一个集合 ，一个数域 和一个二元运算（这个符号也称为李括号）组成。如果它们满足以下几条性质，称为一个李代数，记作 

1、封闭性

2、双线性

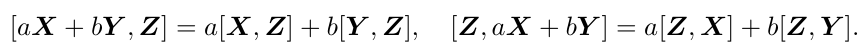
3、自反性

4、雅可比等价

 

李群与李代数的关系

考虑相机旋转，由于是旋转阵是正交阵，满足下式

上式两边对t求导，整理得

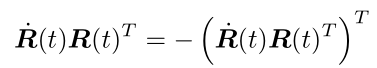
可以看出，是反对称矩阵，运用反对称矩阵的映射符号^，上式改写为

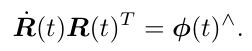
等式两边右乘

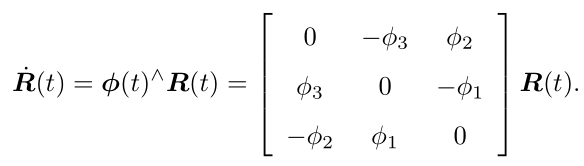
可以看到，每对旋转矩阵求一次导数，只需左乘一个

设，将在附近进行一阶泰勒展开

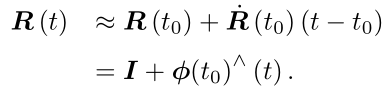，其中反映了的导数性质，故称它在原点附近的正切空间

在附近，可以设不变（小范围内化曲为直），因此

解方程得

，其中初值条件为

上式表明了旋转矩阵与反对称矩阵在工作点附近是指数/对数的关系。事实上，是李群上的元素，而则是对应到李代数上的元素

 

 

 

李代数so（3）

设

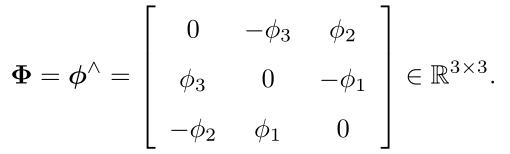
则定义如下

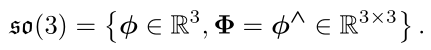
两个向量的李括号为

 

李代数se（3）

设

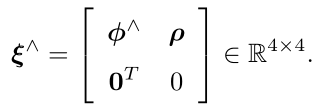，其中表示平移（但不是平移向量t，与之相差一个系数）

则定义如下

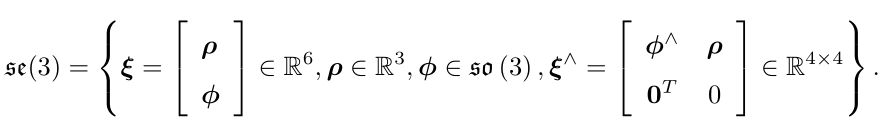
李括号为

 

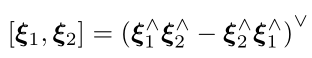
指数与对数映射

so（3）的指数映射

任何一个矩阵指数映射（设收敛）都可以写成泰勒展开

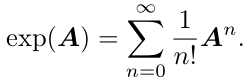
因此，对于so（3）的任一元素，可定义它的指数映射如下

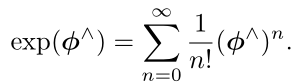
是一个三维向量，定义其模长和方向分别为和，则。反对称矩阵有以下性质

利用这些性质推导矩阵指数映射

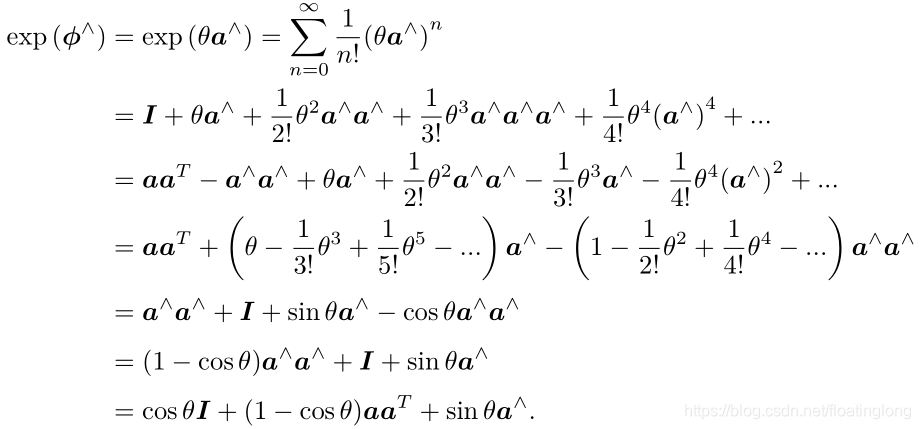
上式实际上也是罗德里格斯公式，因此李代数so（3）实际上就是旋转向量组成的空间，其指数映射就是罗德里格斯公式，通过这个公式可以对应到李群SO（3）中的旋转矩阵，反过来也可以从李群对应到李代数

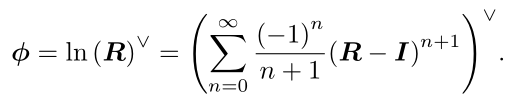
对于这个式子，利用迹的性质分别求解转角和转轴更为简便。

另外，每个SO（3）的元素都存在与之对应的so（3）元素，但可能存在多个so（3）元素与之对应。例如，对于旋转角θ，θ与θ+360°其意义是一样的（具有周期性）。如果将θ取值范围限制在-180°~+180°，则对应关系是一一对应的。

 

se（3）的指数映射

se（3）的指数映射形式如下（推导过程与so（3）类似）

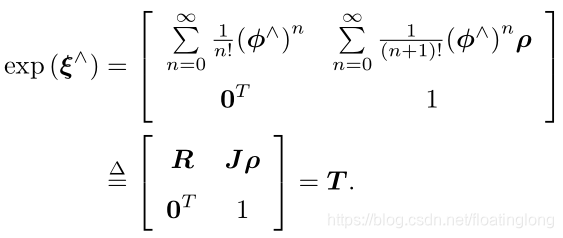
其中

J的推导如下

 

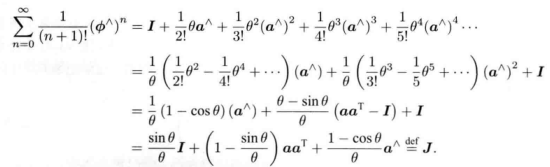
SO（3）与so（3）、SE（3）与se（3）的关系总结如下

 

 

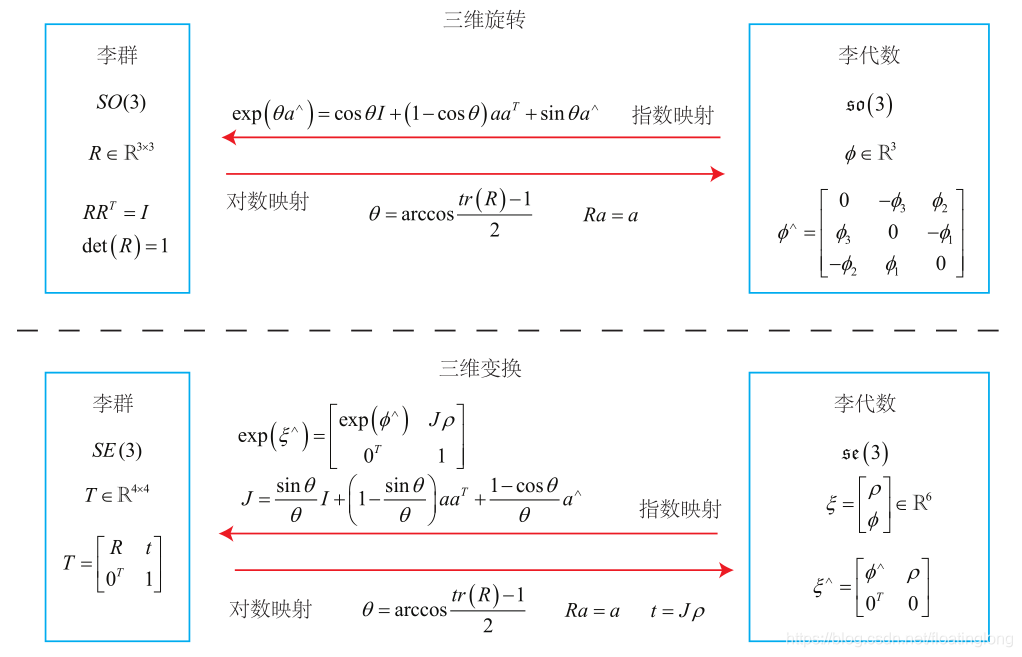
李代数求导与扰动模型

BCH 公式与近似形式

两个李代数指数映射乘积的完整形式由BCH公式给出，它展开的前几项为

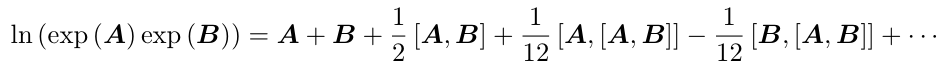
当或为小量时，近似表达式如下

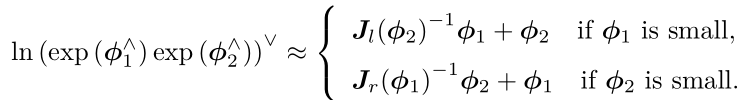
该式告诉我们，当对一个旋转矩阵R2左乘一个微小旋转矩阵R1（李代数为）时，可以近似地看作，在原有的李代数上，加上了一项。同理，第二个近似描述了右乘一个微小位移的情况。因此李代数在 BCH
近似下，分成了左乘近似和右乘近似两种

左乘雅可比

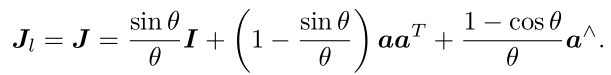
它的逆

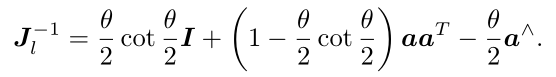
右乘雅可比

 

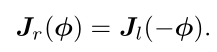
对于SO（3）和so（3），考虑某个旋转R，左乘上微小旋转△R，在李群上是△RR，用李代数表示为

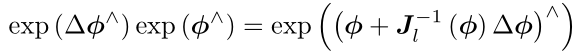
反之，在李代数进行和的加法，可近似为李群上带雅可比的乘法

对于SE（3）和se（3），BCH近似公式如下（是一个6*6矩阵）

 

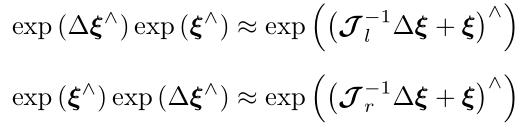
李代数求导

利用李代数求导有两种思路：

1、用李代数表示姿态，然后根据李代数加法对李代数求导（李代数的求导模型）

2、对李群左/右乘微小扰动，对该扰动求导（左/右扰动模型）

 

李代数的求导模型

在SO（3）上，考虑一个空间点p进行旋转R，得到Rp，计算旋转之后点的坐标相对于旋转的导数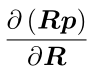

由于 SO(3) 没有加法，所以该导数无法按照导数的定义进行计算。设R对应的李代数为，转而计算（旋转之后点的坐标相对于李代数的导数）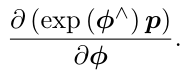

过程如下

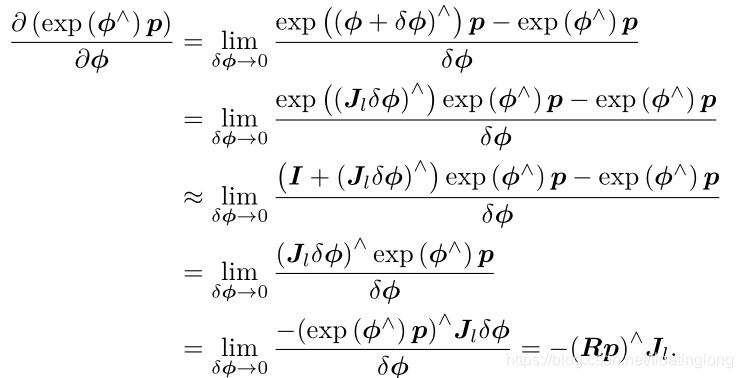
第一行的等号是导数定义，第二行的等号运用了BCH公式，第三行约等号进行泰勒展开，第五行等号利用外积的性质

 

扰动模型

在SO（3）上，考虑一个空间点p进行旋转R，并左乘微小扰动△R，设△R对应李代数为，则

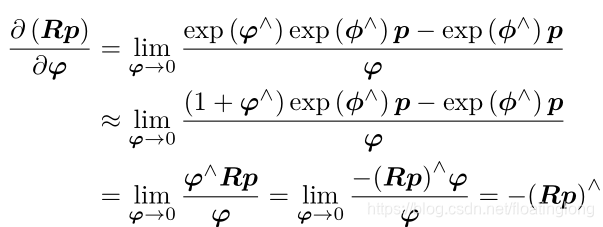，该式比起李代数的求导模型，省去一个雅可比的计算

 

在SE（3）上，考虑一个空间点p进行变换T，并左乘微小扰动△T，设，其中，则SE（3）的扰动模型

，其中符号将齐次坐标的空间点变换成一个 4×6的矩阵