宽调谐低功耗差分环形VCO设计

用于宽调谐范围和低功耗应用的差分环形压控振荡器的设计与 分析

摘要

压控振荡器（VCO）是所有无线通信系统所需的基本组件。本文提出了一种 用于宽调谐范围的具有两个控制电压的四级差分环形压控振荡器。该压控振 荡器采用双延迟环技术以实现高工作频率。此外，在提出的压控振荡器延迟 单元的下拉网络中串联了一个低阈值电压的NMOS晶体管，以实现低频振荡。 所提出的压控振荡器在Cadence软件中基于65纳米台积电CMOS工艺、1.2 伏电源电压条件下进行了版图前仿真。提出的压控振荡器的调谐范围从1兆 赫至13.8吉赫，相比其他工作提升了19.77%。该低功耗压控振荡器的功耗范 围为29.3 μW至1.715毫瓦。在5.161吉赫中心频率下，1兆赫偏移频率处的相 位噪声为 −82.3 dBc/Hz，10兆赫偏移频率处的相位噪声为 −106.9  dBc/Hz，其面积为102.457 μm²。与其它环形振荡器相比，该设计在低功耗 和面积方面表现出更多优势。

关键词 差分环形压控振荡器，低功耗，宽调谐范围

1 | 引言

近年来，具有宽调谐范围的高速无线通信系统受到了广泛关注。在现代无线通信系统中，锁相环（PLL）起着关键 作用。1 PLL 系统由相位检测器（PD）、环路滤波器（LF）、电荷泵（CP）和压控振荡器（VCO）组成。压控振 荡器（VCO）是锁相环中最关键的部分，因为它直接提供锁相环的输出信号。锁相环是一种闭环反馈系统，当其处 于锁定状态时，能够估计输入信号的频率和相位角。另一方面，振荡器是一个带有正反馈环的放大器，其频率是电 压的函数。2-7

压控振荡器（VCO）可分为两种类型：电感电容压控振荡器（LC‐VCO）和环形压控振荡器（ring‐VCO）。1 每种类型具有不同的频率调谐方法。例如，可变输出电容、电流导向和锁存控制用于环形振荡器的频率变化，而可 变电容或可变电感则用于电感电容压控振荡器（LC‐VCO）的频率变化。电感电容压控振荡器（LC‐VCO）是射频 应用（RF）的最佳选择，具有最高分辨率和频率，但其存在有限调谐范围和大芯片面积的问题。另一方面，环形压 控振荡器（ring‐VCO）具有诸多优势，如宽调谐范围、小面积、易于集成、多相时钟产生以及在低功耗下提供高 频输出。然而，环形压控振荡器（ring‐VCO）存在相位噪声性能差和低分辨率的问题。8-13

环形压控振荡器（ring‐VCO）分为两类：单端型和差分型。在差分型环形压控振荡器（DRO）中，延迟单元 的数量可以是奇数或偶数；而对于单端环形压控振荡器（SERO），延迟单元的数量必须为奇数。根据巴克豪森准 则，每个单元应提供180°/N的相位，其中N为环形压控振荡器中的延迟单元数量。相比SERO，DRO更为常用，因 其具有诸多优势，例如可使用奇数或偶数个单元、对共模噪声具有更强的抗干扰能力、较低摆幅以及输出具有50% 占空比。此外，在DRO中实现高频性能，并同时获得同相和正交输出也较为容易。14-21

过去，DRO设计人员一直在努力改进设计DROs中的重要参数，例如相位噪声、功耗、工作电压、占用面积、 振荡频率、多相时钟产生、电源敏感性以及调谐范围。因此，提出了不同的DRO拓扑结构以改善这些参数。刁和薛 22提出的基于Park‐kim延迟单元的DRO提供了宽频率范围和全范围控制电压；然而，其功耗较高。埃肯和宇川 23提出的基于电压和电流控制延迟单元的DRO能够产生高频输出和宽调谐范围，但存在相位噪声性能差和高功耗的 问题。帕尔维齐等人24提出的基于对称负载延迟单元的DRO主要特点是在低电压下实现宽调谐范围；然而，该振荡 器的相位噪声性能较差。卢等人25提出的采用锁存对延迟单元的DRO除了具有良好的相位噪声和宽调谐范围外，还 表现出控制电压的良好调谐线性度，但导致了高功耗和低频问题。李等人26提出的基于注入锁定技术延迟单元的 DRO是另一种具有可扩展性、宽工作频率范围和低相位噪声的DRO，但尽管具备这些优点，其功耗仍然较高。 Sanchez‐Azqueta等人27提出的基于经典全差分延迟单元的DRO拓扑结构可以显著节省面积并降低功耗，但代价 是频率范围较窄。涂等人28提出的基于并联‐并联反馈延迟单元的DRO不仅改善了调谐频率范围，还提高了输出信号 摆幅并降低了功耗。刘等人29提出的采用推挽反相器延迟单元实现的DRO提供了高频，但也带来了频率调谐范围有 限、相位噪声性能差和高功耗等问题。李和林30提出了一种基于交叉耦合对称负载延迟单元的DRO，具有宽频率范 围、良好线性度和低功耗的特点。法斯等人31提出的基于可编程电阻网络延迟单元的DRO具有宽频率范围，但其功 耗较高。尹等人32提出的基于延迟单元实现的宽调谐范围DRO具有良好的相位噪声性能；然而，高功耗和大芯片面 积成为该DRO的关键缺点。德马蒂诺斯等人33提出的DRO表现出宽频率范围，但另一方面其功耗更高。

本文提出了一种四级差分环形振荡器。在该压控振荡器中，采用了多种技术来扩大频率范围。它具有宽调谐范 围、高频、低功耗和小占用面积的特点。

本文的结构如下：第2节描述了提出的压控振荡器。仿真结果在第4节中给出。最后，第5节对论文进行了总结。

2 | 基于DR0的压控振荡器设计

在差分型环形压控振荡器中，级数可以为奇数或偶数。但增加级数会导致功耗、面积和成本的增加。因此，两级、 三级或四级差分型环形压控振荡器更为常见。两级和四级差分型环形压控振荡器能够产生正交输出，但如果振荡频 率是关键因素，则三级差分型环形压控振荡器比四级更为合适。虽然采用两级差分型环形压控振荡器似乎可降低功 耗，但在设计两级差分型环形压控振荡器时，为了满足巴克豪森准则，每个单元需要附加相移。另一方面，实现适 当的相移会消耗额外的功率。34

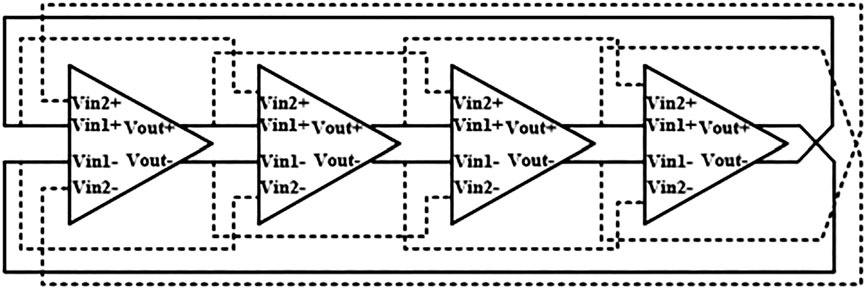
提出的四级差分环形振荡器如图1所示。在此差分环形振荡器中，采用了用于高工作频率的双延迟环路方案。该 双延迟环路由具有较高延迟的主延迟路径和具有较低延迟的次级延迟路径组成。在图1中，虚线表示次级延迟路径， 实线表示主延迟路径。此差分环形振荡器中的每个四级延迟单元都有两个差分主输入电压Vin1+和Vin1−，两个差 分次级输入电压Vin2+和Vin2−（其相位早于Vin1+和Vin1−），以及两个差分输出电压Vout1+和Vout1−。在 提出的差分环形振荡器的延迟单元中，Vin1+和Vin1−来自前一级延迟单元的Vout1+和Vout1−，而Vin2+和 Vin2−连接到前两级延迟单元的Vout1+和Vout1−。

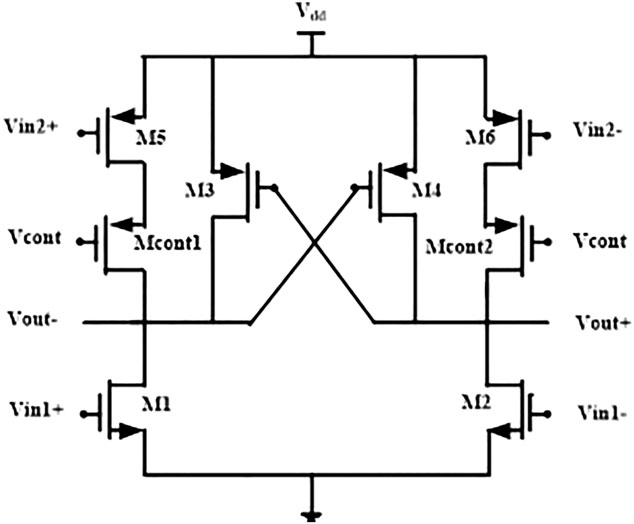
金等人38中提出的VCO的延迟单元结构如图2所示。图2中的差分延迟单元中，M1和M2为差分输入NMOS晶 体管，其栅极连接至主输入。M3和M4为交叉耦合PMOS晶体管，M5和M6为连接到次级延迟路径的PMOS输入晶 体管，Mcont1和Mcont2为PMOS控制晶体管，其作用是通过改变控制电压来调节DRO振荡的频率。每个单元具 有两个差分输出，该差分环形振荡器共产生八个输出相位。

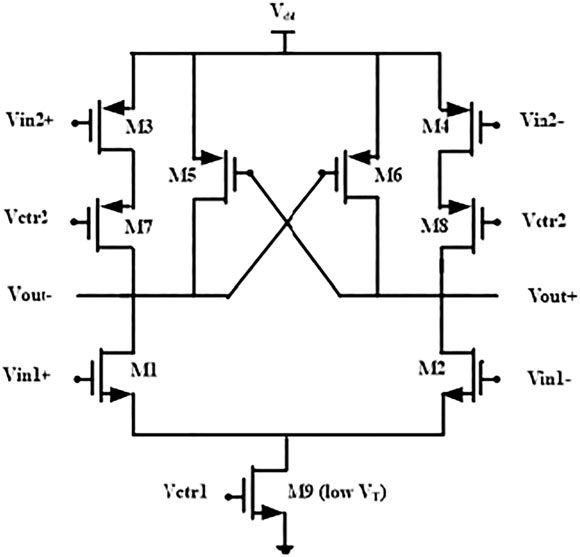
通过借鉴金等人38所采用的技术，提出了如图3所示的具有两个控制电压的延迟单元。在该延迟单元中，M1和 M2是主环路的差分输入NMOS晶体管，M5和M6是交叉耦合负载PMOS晶体管，用于提供正反馈锁存并增大摆幅， 它们连接至Vdd；M3和M4是差分输入PMOS管。PMOS的性能通常比NMOS慢。因此，在提出的延迟单元中，为 了补偿M3和M4这两个PMOS的性能，将它们的输入连接到次级输入。在该延迟单元中，为了实现宽频率范围，采 用了两个控制电压。M7、M8和M9为控制晶体管，其中M7和M8的PMOS晶体管输入连接至控制电压Vctr2， M9的NMOS晶体管输入连接至控制电压Vctr1。M7和M8的控制PMOS晶体管用于获得高频。另一方面，M9的 NMOS控制晶体管是低阈值电压NMOS，用于实现低频。此外，Vctr1必须大于M9的VT，以保持M9晶体管处于导 通状态；而当VT变小时，Vctr1也可以设置为更小的值。因此，在提出的延迟单元中，为了增加Vctr1的变化范围 以及提出的压控振荡器的频率变化范围，使用了低‐VT NMOS晶体管M9。

当Vctr2设置为高电平时，通过增加Vctr1的电压值，可以增加M9的驱动电流。因此，提出的延迟单元的负载 电容的放电速度增加。结果，延迟单元的延迟减小，从而提出的压控振荡器频率增加。当Vctr1设置为高电平时， 通过降低Vctr2，M7和M8更加导通，连接到

次级输入开始增加。随着M3和M4作用的增强，第二路径对延迟单元的影响也随之增加。因此，提出的延迟单元的 下拉网络的驱动电流增大。从而，提出的延迟单元的负载电容可以更快地充电。这种负载电容充电速度的提高最终 导致延迟单元的延迟降低，并进而提高提出的压控振荡器的频率。

提出的压控振荡器单元中使用的晶体管尺寸在表1中给出。

3 |频率分析

在哈菲兹和杨39以及孙和克瓦什涅夫斯基40的研究中，提出了一种具有任意耦合结构的多路径环形振荡器的通用模 型，用于计算振荡频率。此外，哈菲兹和杨39以及孙和克瓦什涅夫斯基40确定了振荡频率作为级数和延迟环的函数。 另一方面，在提出的论文中，进行了一项分析，以研究影响提出的延迟单元输出电压变化速度的因素。

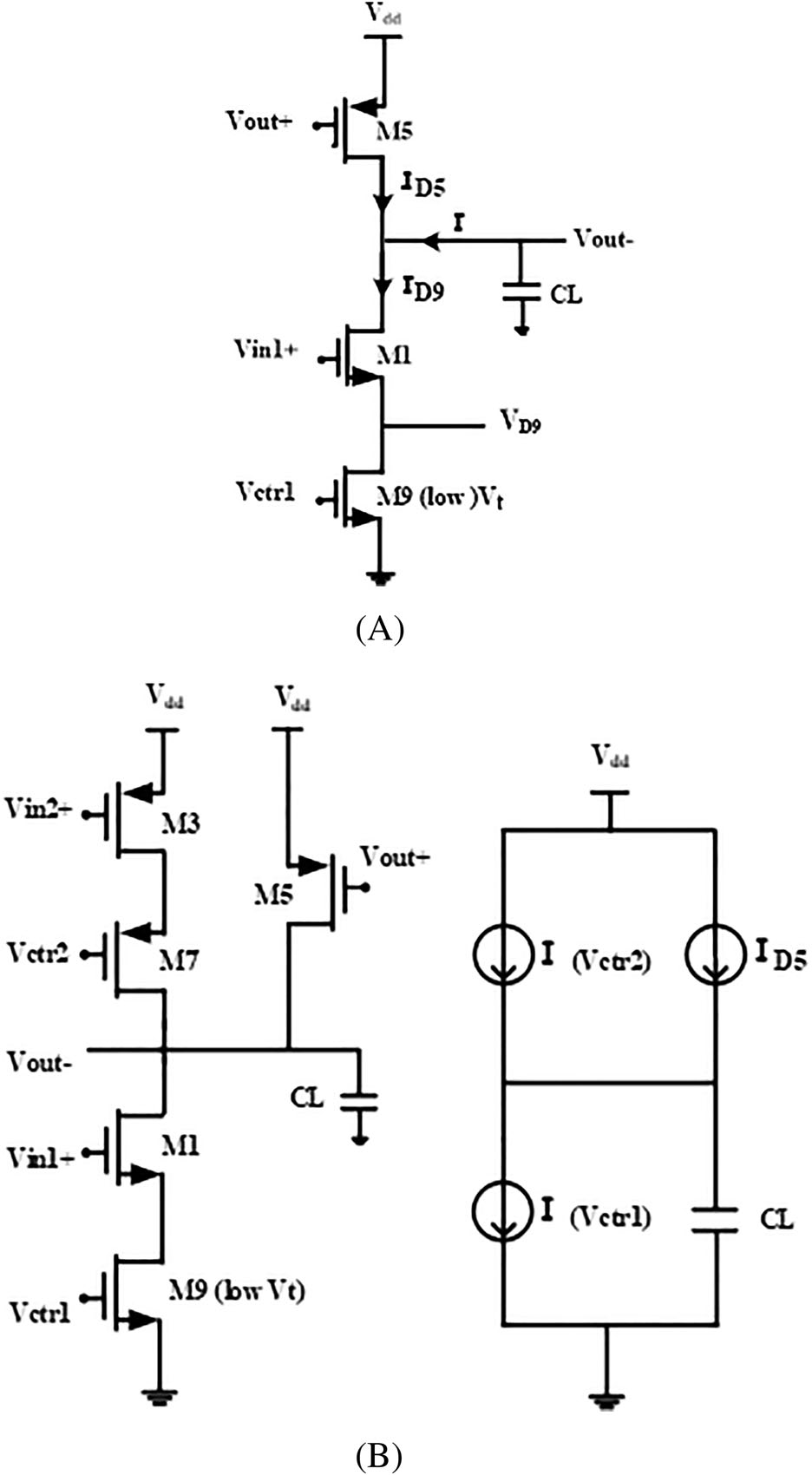
提出的压控振荡器工作在两种不同模式下：低频模式和高频模式。在低频模式下，输出波形为方波。为了在提 出的压控振荡器中实现低频，应消除晶体管M3和M4的影响，因为提出的延迟单元的次级输入（会提高压控振荡器 的速度）施加在这些晶体管上。为此，Vctr2的输入被设置为高电平。在这种情况下，等效半电路如图4A所示。

在Vin1+的低到高跳变过程中，延迟单元表现出三个工作区域。在第一个区域中， |VGS5| 为Vdd，因此M5导通。 由于M1的输入为低电平，VGS1低于VTn（NMOS晶体管的阈值电压），所以该晶体管关断。在此区域中，I = − ID5，因此根据公式1，I与Vctr1的变化无关。

$$
ID5 = \mu_p C_{ox} \frac{W_9}{l_9} \left[(V_{out+}) - V_{dd} - V_{Tp}\right] \left[(V_{out-}) - V_{dd}\right] - \frac{1}{2} \left[(V_{out-}) - V_{dd}\right]^2
$$

在第二个区域， |VGS5 | 高于 |VT p | （PMOS晶体管的阈值电压），该晶体管处于导通状态；另一方面，V GS1 高于V Tn ， M1也处于导通状态。因此在第二个区域，I= I D9( Vctr1)− I D5 ，根据公式1和2，I D5 与Vctr1的变化无关，而I D9 则依赖于 该变化。

$$
ID9(vctr1) = \mu_n C_{ox} \frac{W_9}{l_9} (V_{ctr1} – V_{Tn_low}) (V_{D9}) - \frac{1}{2} V_{D9}^2
$$

因此，I 依赖于 Vctr1，且随着 Vctr1 增大，I 也随之增大。另一方面，根据公式2、3和4，若增加 Vctr1，则 可减小单元延迟。

$$
I \Delta t = C_L \Delta V_{out-} = C_L \frac{V_{dd}}{2}
$$

$$
\Delta t = \frac{C_L V_{dd}}{2I}
$$

在第三区域， |VGS5| 低于 |VTp| ，M5关断，而VGS1高于VTn ，M1导通。因此I= ID9(Vctr1)，所以根据公式 2，在此区域电流I依赖于Vctr1，但在此区域中的依赖性比第二区域更强。在第三区域，根据公式2、3和4， Vctr1的增加将导致延迟单元的延迟减小，并使提出的压控振荡器的频率增加。

在所有三个区域中，VCO输出频率与Vctr2无关。为了实现低频，将Vctr2设置为高电平，仅通过改变Vctr1来调节 VCO频率。此外，根据公式2，在提出的延迟单元中，M9使用低‐VT的NMOS晶体管会导致Vctr1变化范围的增加。

在高频情况下，提出的压控振荡器的等效半电路如图4B所示。在这种情况下，普通环形振荡器的振荡频率可以 通过大信号模型来定义

$$
f_{osc} = \frac{1}{N (t_{rise} + t_{fall})}
$$

其中，N 是环形振荡器的级数，trise  是输出信号的上升时间，tfall  是输出信号的下降时间。对于该延迟级，trise  和  tfall  可以从

$$
I_{discharge} = C_L \frac{d V_{out}}{dt} \Rightarrow \int_{0}^{t_{rise}} \frac{I_{D9}(V_{ctr1}) - I_{D5}}{C_L} dt = \int_{0.1V_{dd}}^{0.9V_{dd}} d V_{out} \Rightarrow t_{rise} = \frac{0.8 C_L V_{dd}}{I_{D9}(V_{ctr1}) - I_{D5}}
$$

$$
I_{charge} = C_L \frac{d V_{out}}{dt} \Rightarrow \int_{0}^{t_{fall}} \frac{I_{D7}(V_{ctr2}) + I_{D5}}{C_L} dt = -\int_{0.9V_{dd}}^{0.1V_{dd}} d V_{out} \Rightarrow t_{fall} = \frac{0.8 C_L V_{dd}}{I_{D7}(V_{ctr2}) + I_{D5}}
$$

因此，上升和下降转换的贡献被包含在公式8中：

$$
f_{osc} = \frac{1}{1.6 N C_L V_{dd}} \left[ \frac{1}{I_{D9}(V_{ctr1}) - I_{D5}} + \frac{1}{I_{D7}(V_{ctr2}) + I_{D5}} \right] = \frac{(I_{D9}(V_{ctr1}) - I_{D5})(I_{D7}(V_{ctr2}) + I_{D5})}{1.6 N C_L V_{dd} (I_{D9}(V_{ctr1}) + I_{D7}(V_{ctr2}))}
$$

为了实现提出的压控振荡器的高频，将Vctr1设置为高电平，从而使M9的电阻保持最小。随着M9的电阻减小， 负载电容（CL）的放电路径的电阻也随之减小，CL的放电电流相应减少。因此，根据公式4，提出的延迟单元的延 迟减小，压控振荡器的频率增加。公式8和图4表明输出频率取决于控制电压。另一方面，在高频情况下，由于 Vctr1保持为高电平不变，输出频率仅通过改变Vctr2来调节。

在公式8中，振荡频率似乎与Vdd成反比，但这是不正确的。根据公式8，振荡频率与ID5成正比。另一方面，根 据公式1，ID5与Vdd呈二次关系。因此，根据公式8，振荡频率与Vdd成正比。

输入PMOS M3的栅极连接到Vin2+的次级输入。因此，与连接到主输入的输入NMOS M1相比，PMOS M3更 早接收到其输入，这可以补偿PMOS速度限制。结果，提出的延迟单元的延迟减小，压控振荡器频率增加。另一方 面，通过降低Vctr2，M7晶体管被导通。在这种情况下，晶体管M3的作用增强。由于

次级输入提高了压控振荡器的速度，通过增强M3晶体管的作用，压控振荡器输出频率增加。相反，通过降低 Vctr2并随后减小次级输入对延迟单元的影响，压控振荡器的频率降低。

4 |仿真结果

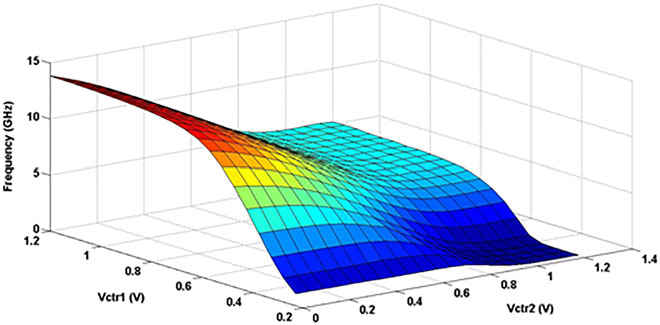
基于所提出的DRO的VCO在Cadence软件中采用65纳米台积电CMOS工艺、1.2伏电源电压下进行仿真。图5显示 了频率变化随Vctr1和Vctr2变化的三维图形。当Vctr2固定在1.2 V时，通过将Vctr1从0.23 V调节到1.2 V，所提出 的VCO频率从1兆赫变化到5.161吉赫；而当Vctr1固定在1.2 V时，通过将Vctr2从1.2 V调节到0 V，VCO频率从 5.161吉赫变化到13.8吉赫。因此，该VCO的振荡频率范围可从1兆赫至13.8吉赫，频率范围达13.799吉赫（99.99%）。

另一方面，从图5可以看出，在低频区域，基于Vctr2的频率变化较小。此时，Vctr1和Vctr2可分别用于粗调和细调 频率变化。在高频区域，这两个控制电压的作用互换，即基于Vctr1的频率变化较小，而通过调节Vctr2可观察到更 大的频率变化。换句话说，在高频区域，Vctr1可用于细调，Vctr2用于粗调。在中频区域，根据Vctr1和Vctr2的具 体取值，二者可能分别承担粗调或细调的作用。

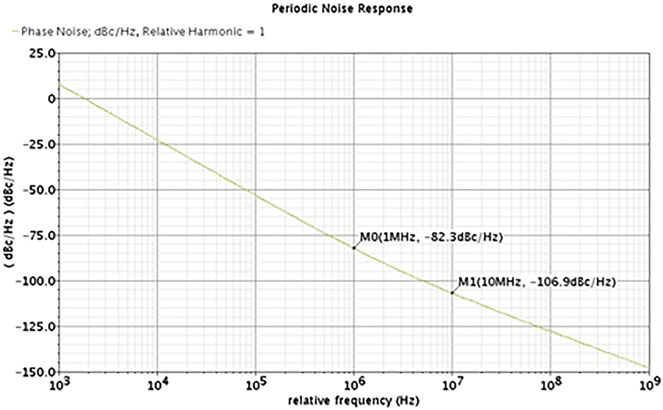
如图6所示，提出的压控振荡器在5.161吉赫中心频率下，于1兆赫偏移频率处的相位噪声达到 −82.3 dBc/Hz， 在10兆赫偏移频率处为−106.9 dBc/Hz（Vctr1= 1.2，Vctr2= 1.2）。

提出的压控振荡器的功耗在1.715毫瓦到29.3 μW之间变化。

为了在不同中心频率下与其他压控振荡器进行更好的比较，通常使用根据公式9计算的品质因数（FOM）34：

$$
FOM = L{f_{Off}} - 20 \log \frac{f_{OSC}}{f_{Off}} + 10 \log \frac{P}{1mW}
$$

其中，L{fOff} 是振荡器在偏移频率 (fOff) 处的相位噪声，单位为 dBc/Hz，fosc  为中心频率，Pdiss  为以毫瓦为单位 的功耗。但该品质因数方程并不够全面。因此，本文为了改进品质因数，使其能更有效地比较压控振荡器参数，在 公式9中增加了频率范围和占用面积两个项，从而得到公式10所示的品质因数表达式：

$$
FOM = L{f_{Off}} - 20 \log \frac{f_{OSC}}{f_{Off}} - 20 \log \left[ \frac{100(F_{MAX} - F_{MIN})}{F_{MAX}} \right] + 10 \log \frac{P}{1mW} + 2 \log \frac{area}{1\mu m^2}
$$

其中，FMAX为最大频率，FMIN为最小频率，area为以平方微米为单位的占用面积。所提出的压控振荡器的计算品 质因数为 −193.573 dBc/Hz。

对提出的压控振荡器进行了工艺、电压和温度（PVT）变化分析，以评估其PVT敏感性。PVT变化的仿真结果 列于表2中。在此分析中，对调谐范围、中心频率和功耗进行了仿真。从表2可以看出，随着温度升高，提出的压控 振荡器的调谐范围、fosc和功耗均下降。另一方面，这三个参数随电源电压的增加而增加。此外，提出的压控振荡器 在快最佳模式下的调谐范围、fosc和功耗大于典型模式，而在典型模式下又大于慢最差模式。这些PVT变化结果是可 接受的。

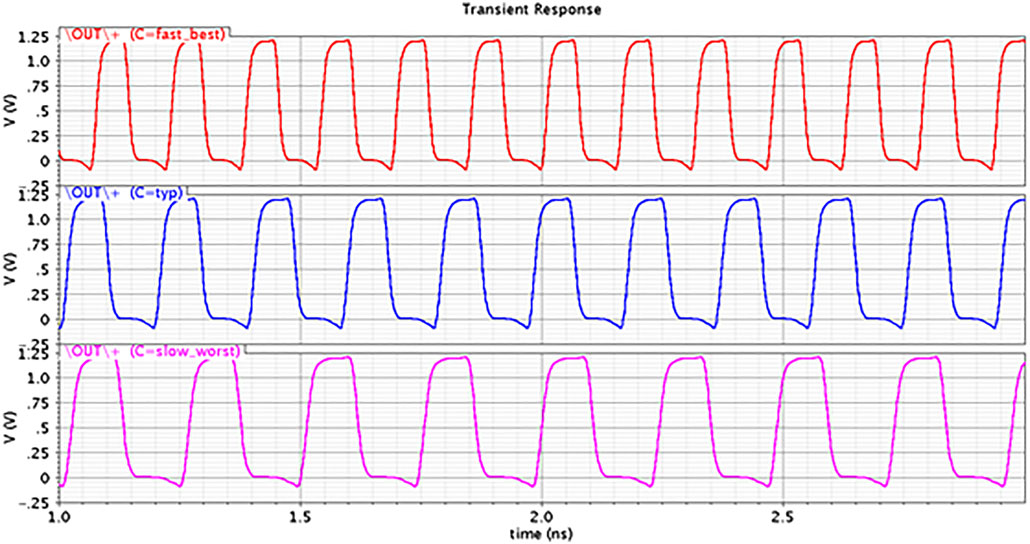
在 −25°C下的快速‐最佳、75°C下的慢速‐最差以及27°C典型模式下，且在1.2V电源电压条件下，提出的压控振 荡器中心频率的波形如图7所示。

在表3中，将提出的压控振荡器前布局仿真性能与采用65纳米技术的其他近期压控振荡器进行了比较。在压控 振荡器中使用具有较大 W/L比值的晶体管可改善相位噪声，但会增加有源面积和功耗。在提出的压控振荡器中，采 用了较小的晶体管以降低功耗和有源面积。从该表可以看出，提出的压控振荡器具有非常低的功耗和面积。本设计 的调谐范围相比表中其他工作提高了19.77%，同时表现出可接受的相位噪声。在该表的最后一列中，使用本文提出 的改进的优值计算了各压控振荡器的品质因数。该表中，提出的压控振荡器及之前工作中提出的压控振荡器1,36,37 具有仿真结果，而表中的其他压控振荡器则提供了测量结果。

结论

本文提出了一种用于四级压控振荡器的新型多路径延迟单元，具有宽频率调谐范围，并采用两个控制电压来调节频 率。该延迟单元中使用了低阈值NMOS晶体管，以实现宽调谐范围。此外，本文还对影响提出的延迟单元输出电压 变化速度的因素进行了理论分析。提出的压控振荡器在1.2伏电源电压下，采用Cadence软件和65纳米台积电 CMOS工艺进行仿真。该压控振荡器具有1兆赫至13.8吉赫（99.99%）的宽调谐范围，在5.161吉赫中心频率处，1 兆赫偏移频率下的相位噪声为 −82.3 dBc/Hz，10兆赫偏移频率下的相位噪声为 −106.9 dBc/Hz，功耗低至0.785毫 瓦，占用面积小至102.457 μm²。因此，该振荡器适用于高频、宽频率范围、低功耗和小面积的应用。

| 表1 提出的压控振荡器单元中所用晶体管的尺寸（l = 65 nm） |
| :— | :— | :— |
| 晶体管名称 | M1, M2, M3, M4, M7, M8 | M5, M6 | M9 |
| 晶体管宽度， μm | 1.56 | 0.91 | 3.12 |

| 表2 工艺、温度和电压变化下VCO参数的变化 |
| :— | :— | :— | :— | :— | :— | :— | :— | :— | :— | :— |
| 参数 | 温度变化(Vdd= 1.2 V) | | | 电压变化(T= 27°C) | | | | 工艺变化(Vdd= 1.2 V) | | |
| | T= −25°C | T= 0°C | T= 75°C | V= 1 V | V= 1.1 V | V= 1.2 V | V= 1.3 V | 慢-最差(process= slow NMOS and PMOS; T= 75°C) | 典型 (T= 27°C) | 快-最佳(process= fast NMOS and PMOS; T= −25°C) |
| 调谐范围, GHz | 0.276 × 10⁻³ − 14.58 | 0.505 × 10⁻³ − 14.16 | 8.12 × 10⁻³ − 13.08 | 0.965 × 10⁻³ − 10.75 | 0.984 × 10⁻³ − 12.28 | 1 × 10⁻³ − 13.8 | 1.019 × 10⁻³ − 15.08 | 0.994 × 10⁻³ − 11.14 | 1 × 10⁻³ ‐ 13.8 | 1.02 × 10⁻³ ‐ 16.89 |
| f _osc , GHz (Vctr1= 1.2 V, Vctr2= 1.2 V) | 5.478 | 5.321 | 4.945 | 3.93 | 4.563 | 5.161 | 5.725 | 4.109 | 5.161 | 6.634 |
| P _diss , mW | 0.802 | 0.799 | 0.770 | 0.413 | 0.582 | 0.785 | 1.024 | 0.634 | 0.785 | 0.964 |

| 表3 性能对比 |
| :— | :— | :— | :— | :— | :— | :— | :— | :— | :— |
| 参考文献 | 技术, nm | 电源, V | 级数 | 调谐范围, GHz | 有源面积, μm² | f _osc , GHz | 相位噪声, dBc/Hz @ 1 MHz | P _diss , mW | FOM, dBc/Hz | 结果 |
| Kamran and Ghaderi ³⁶ | 180 | 1.8 | 3 | 3.1‐10.1(69.3%) | ‐ | 6.6 | −113 | 6.01 at maximum frequency | ‐ | 仿真 |
| Chien et al ¹³ | 20 | 1.25/1.1 | 4 | 2‐16(87.5%) | 44 × 10³ | 15 | −136.6 at 10 MHz | 46.2 | −212.395 | 测量 |
| Sharma and Biswas ²⁰ | 65 | 0.7 | 3 | 0.83‐3.77(77.98%) | 67.65 | ‐ | ‐ | 26.73 × 10⁻³ | ‐ | 测量 |
| Yoo et al ³² | 65 | 1.2 | 2 | 2‐8(75%) | 38 × 10³ | 4.2 | −101 | 6.4 | −193.744 | 测量 |
| Sun and Jiang ³⁷ | 180 | 1.2 | 3 | 0.261‐1.32(80.22%) | 5.175 × 10³ | 0.73 | −98 | 0.41‐1.6 | −189.796 | 仿真 |
| Kim et al ³⁸ | 65 | 1 | 4 | 0.48‐1.01(52.47%) | 22.54 × 10³ | 0.645 | −110.8 | 10 | −182.689 | 测量 |
| Mishra and Sharma ¹ | 180 | 1.8 | 3 | 1.0229‐3.995(74.39%) | ‐ | 3.995 | −80.17 | 7.49 | ‐ | 仿真 |
| Vornicu et al ²¹ | 180 | 1.8 | 4 | 0.4‐0.85(52.94%) | 812 | 0.85 | −102 at 2 MHz | 1.17 | −182.38 | 测量 |
| Demartinos et al ³³ | 65 | 1.2 | 4 | 1.55‐3.9(60.25%) | ‐ | 3 | −94 | 7.68 | ‐ | 测量 |
| 本工作 | 65 | 1.2 | 4 | 0.001‐13.8(99.99%) | 102.457 | 5.161 | −82.3 | 0.785 | −193.573 | 仿真 |