84 柱状图中的最大的矩形（单调栈）-优快云博客

本文链接：https://blog.youkuaiyun.com/fffffall/article/details/134297227

文章描述了如何通过动态规划和栈的方法解决柱状图中找到能够勾勒出的最大矩形面积问题，使用了两个指针l和r来记录每个高度对应的左右边界，最终返回最大面积。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

柱状图中的最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

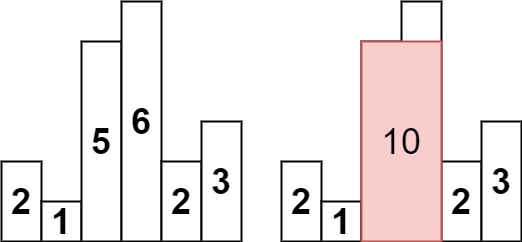
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

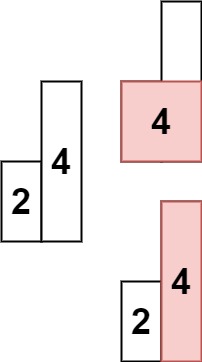
输入： heights = [2,4]
输出： 4

提示：

1 <= heights.length <=105
0 <= heights[i] <= 104

题解

枚举高度+预处理l r

class Solution {
    public int largestRectangleArea(int[] heights) {
        int ans = 0;
        Deque<Integer> st = new ArrayDeque<>();
        int n = heights.length;
        //l[i]为左边最近的比其小的下标 r[i]为右边最近的比其小的下标
        int[] l = new int[n], r = new int[n];
        Arrays.fill(l, -1);// 初始化-1
        Arrays.fill(r, n);// 初始化n
        for (int i = 0; i < n; i++) {
            while (!st.isEmpty() && heights[i] < heights[st.peekLast()]) {
                r[st.pollLast()] = i;
            }
            st.addLast(i);
        }
        st.clear();
        for (int i = n - 1; i >= 0; i--) {
            while (!st.isEmpty() && heights[i] < heights[st.peekLast()]) {
                l[st.pollLast()] = i;
            }
            st.addLast(i);
        }
        for (int i = 0; i < n; i++) {
            int h = heights[i];
            ans = Math.max(ans, (r[i] - l[i] - 1) * h);
        }
        return ans;
    }
}