单调栈：柱状图中最大的矩形（力扣84）

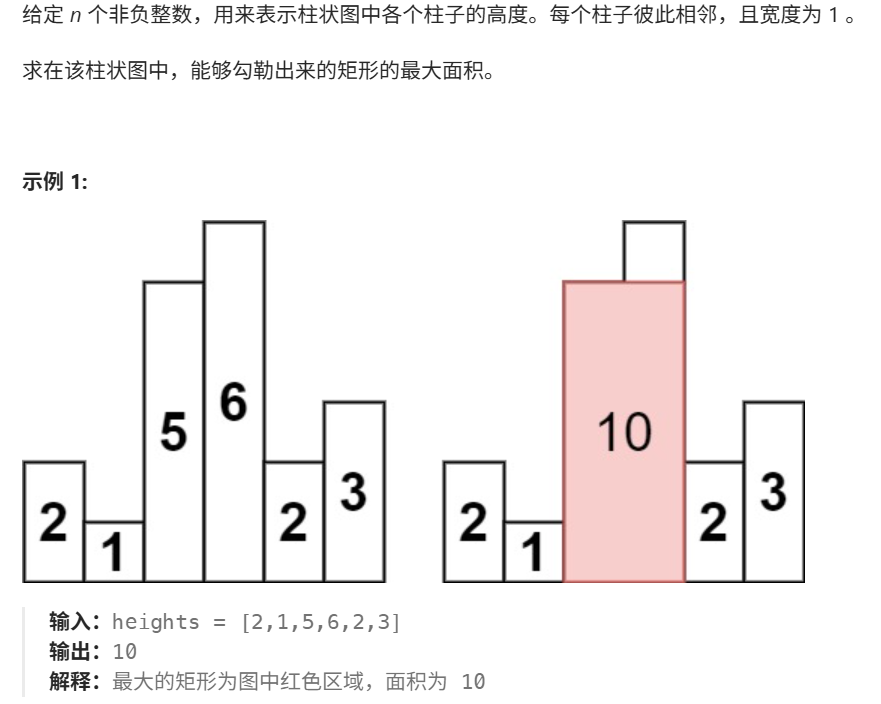
题目描述：

枚举方法

首先对于任意一根柱子i，如果它的两侧柱子都比它高则向两侧延伸形成的矩形面积绝对是变大的。

所以我们只需找到左侧第一个比i小的柱子和右侧第一个比i小的柱子并记录它们的下标，那么以i柱子延伸的最大矩形面积为：（right-left-1)*heights[i]

那么如何找到能作为答案的柱子i呢，很容易想到遍历。

思路：

1、循环体外定义最大值max；

2、遍历数组得到每一根柱子对应的最大延伸后的面积；

3、如果该面积大于max，则赋值给max；

这样还不能得到正确答案，因为忽略了边界值，所以要在数组最左侧和最右侧添加一个负值保证在遍历过程中能够判断到边界值。

代码实现（java）：

class Solution {
  
    public int largestRectangleArea(int[] heights) {
        // 用于记录最大矩形面积
        int max = 0;
        // 获取柱状图的柱子数量
        int n = heights.length;
        
        // 创建一个新数组，在原数组首尾各加一个-1作为哨兵，简化边界判断
        // 首尾的-1确保了所有柱子都能找到左侧和右侧的边界
        int[] temp = new int[n + 2];
        temp[0] = -1;          // 左侧哨兵
        temp[n + 1] = -1;      // 右侧哨兵
        
        // 将原数组的高度值复制到新数组的中间位置（索引1到n）
        for (int i = 0; i < n; i++) {
            temp[i + 1] = heights[i];
        }
        
        // 遍历每个柱子（跳过首尾的哨兵）
        for (int i = 1; i < n + 1; i++) {
            // 左侧边界：从当前位置向左找，直到找到第一个高度小于当前柱子的位置
            int left = i;
            // 右侧边界：从当前位置向右找，直到找到第一个高度小于当前柱子的位置
            int right = i;
            
            // 向左扩展：找到左侧第一个高度小于当前柱子的位置
            // 因为左侧有哨兵-1，循环一定会终止
            while (left >= 1 && temp[left - 1] >= temp[i]) {
                left--;
            }
            
            // 向右扩展：找到右侧第一个高度小于当前柱子的位置
            // 因为右侧有哨兵-1，循环一定会终止
            while (right <= n && temp[right + 1] >= temp[i]) {
                right++;
            }
            
            // 计算当前柱子能形成的最大矩形面积：宽度(right-left+1) * 高度(temp[i])
            // 更新最大面积
            max = Math.max(max, (right - left + 1) * temp[i]);
        }
        
        return max;
    }
}

但是此方法耗时较高，发现无法通过leecode的全部测试用例。

因此便有了下面的单调栈解法：

单调栈方法：

在枚举方法中用时比较高，最坏情况时间复杂度是o（n^2)

如果能利用单调栈和left、right数组来同时记录每一个下标i柱子对应的左侧第一个小于当前高度和右侧第一个小于当前高度的柱子下标，那么只需遍历一次heights数组便得到了答案max；

思路：

初始化一个栈，可以放入数组的第一位元素下标。

定义一个left数组用于存放左侧小于当前数组元素的最近元素下标。

同样定义一个right数组用于存放右侧小于当前数组元素的最近元素下标。

设原数组下标为i

每次都要对比要进栈的下标对应原数组的值与栈顶元素对应下标对应数组值，如果大于，则给left【i】赋值

即 if（height[i]>height[stack.peek()]) left[i]=stack.peek()

对于left：

i=0：栈为空，原数组下标0进栈

i=1：1<2 下标0出栈，下标1进栈

i=2： 5>1 left[2]赋值 下标2进栈

i=3 :   6>5   left[3]赋值 下标3进栈

i=4:   2<6   下标3出栈  2<5 下标2出栈  2>1  left[4]赋值 下标4进栈

i=5    3>2   left[5]赋值 下标5进栈

这样left数组便初始化完成，类比可以初始化right数组。

注意left数组默认每个值都是-1，right数组默认每个值都是length

代码实现：

public int largestRectangleArea(int[] heights) {
    if (heights == null || heights.length == 0) {
        return 0;
    }

    int n = heights.length;
    int[] left = new int[n];
    int[] right = new int[n];
    Arrays.fill(left, -1);
    Arrays.fill(right, n);

    Deque<Integer> indexStack = new LinkedList<>();

    // 构建 left 数组：每个柱子左边第一个比它矮的柱子的索引
    for (int i = 0; i < n; i++) {
        while (!indexStack.isEmpty() && heights[i] <= heights[indexStack.peek()]) {
            indexStack.pop();
        }
        if (!indexStack.isEmpty()) {
            left[i] = indexStack.peek();
        }
        indexStack.push(i);
    }

    indexStack.clear();

    // 构建 right 数组：每个柱子右边第一个比它矮的柱子的索引
    for (int i = n - 1; i >= 0; i--) {
        while (!indexStack.isEmpty() && heights[i] <= heights[indexStack.peek()]) {
            indexStack.pop();
        }
        if (!indexStack.isEmpty()) {
            right[i] = indexStack.peek();
        }
        indexStack.push(i);
    }

    int maxArea = 0;
    for (int i = 0; i < n; i++) {
        maxArea = Math.max(maxArea, (right[i] - left[i] - 1) * heights[i]);
    }

    return maxArea;
}

后面还可以优化，但主包还没研究