学习日历day03 分治法-归并排序（非递归版）

归并排序的非递归实现

算法思想

非递归实现与递归实现的思想相似。区别在于，非递归是从单个元素的组开始，逐步扩大为2个元素、4个元素的组（二倍数扩大组数），即序列划分过程和递归是相反的。如此继续，直至完成所有元素的归并。

每次数组容量扩大两倍

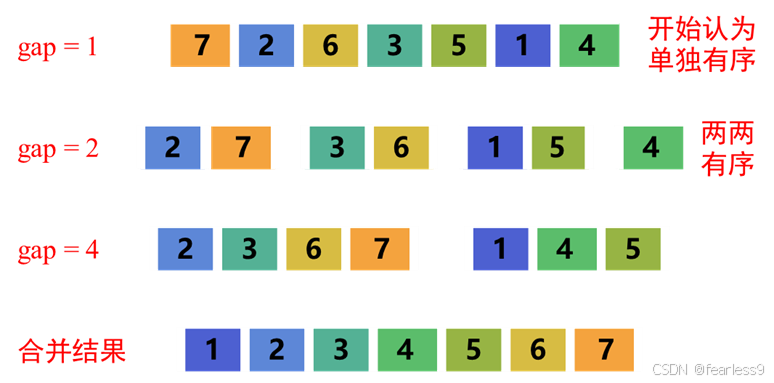实现思路

创建两个函数，一个函数内主要将数组不断扩大，容量从1→2→4→8…直到列表容量扩大到以<len(arr)为边界为止。由两个循环实现，外层循环主要将子数组容量每次扩大两倍；内层循环主要将子数组两两合并，如上图，将27合并，下一次循环将36合并…

代码实现

def merge_sort(arr):
    if len(arr)<=1:
        return arr
    childsize=1
    while childsize<len(arr):#对子数组容量不断循环扩大
        left=0
        while left<len(arr):#两两一组，不断将子数组合并
            mid=min(left+childsize,len(arr)-1)#mid指向第一个列表最后一个孩子的位置，min防止无法凑其两两一组时中间索引越界
            right=min(left+childsize*2-1,len(arr)-1)#right指向第二个列表最后一个孩子的位置，min防止出现无法凑齐两两一组时右边数组越界
            child1=arr[left:mid]
               #为8时    12   12
            child2=arr[mid:right+1]#当数组长度是偶数时执行
               #为8时    12  13
            merge(arr,child1,child2,left)
            left=right+1
        childsize*=2
def merge(arr,left,right,start):
    i=0
    j=0
    sizel=len(left)
    sizer=len(right)
    while i<sizel and j<sizer:
        if left[i]<right[j]:
            arr[start]=left[i]
            i+=1
        else:
            arr[start]=right[j]
            j+=1
        start+=1
    while i<sizel:
        arr[start]=left[i]
        i+=1
        start+=1
    while j<sizer:
        arr[start]=right[j]
        j+=1
        start+=1

a=[33,43,2,5,24,3,73,86,45,23,97,100,8]
merge_sort(a)
print(a)

具体例子

假设有一个数组 arr = [33,43,2,5,24,3,73,86,45,23,97,100,8]，长度为13。

初始状态：

外层while循环思路：

subarray_size = 1 第一次循环时，left 从0开始，每次处理两个大小为1的子数组。

第一次循环： left = 0，mid = min(0 + 1 - 1, 11) = 0，right = min(2 * 1 + 0 - 1, 11) = 1 处理 [33,43] 并合并。

第二次循环： left 从0开始，每次处理两个大小为2的子数组。 left = 0，mid = min(0 + 2 - 1, 11) = 1，right = min(2 * 2 + 0 - 1, 11) = 3 处理 [33,43,2,5] 并合并。

第三次循环： left 从0开始，每次处理两个大小为4的子数组。 left = 0，mid = min(0 + 4 - 1, 11) = 3，right = min(2 * 4 + 0 - 1, 11) = 7 处理 [33,43,2,5,24,3,73,86] 并合并。

第四次循环： left 从0开始，每次处理两个大小为8的子数组。 left = 0，mid = min(0 + 8 - 1, 11) = 7，right = min(2 * 8 + 0 - 1, 11) = 11 处理 [33,43,2,5,24,3,73,86,45,23,97,100,8] 并合并。

通过这种方式，每次循环中子数组的大小都会翻倍，从而逐步合并更大的子数组，直到整个数组被排序。