6.4.2 森林与二叉树的转换

最新推荐文章于 2024-08-17 07:49:52 发布

原创最新推荐文章于 2024-08-17 07:49:52 发布 · 1.3k 阅读

1 ·

CC 4.0 BY-SA版权

数据结构专栏收录该内容

58 篇文章

订阅专栏

本文详细介绍了树与二叉树之间的对应关系，以及如何将森林转换为二叉树和反之的过程。通过将树的根节点视为二叉树的左孩子，兄弟节点视为右孩子的连接，可以建立起两者之间的转换规则。同时，森林到二叉树的转化也遵循类似的原则，将森林中后续树的根节点视为前一棵树的右孩子。这些概念对于理解和操作树形数据结构至关重要。

1、树与二叉树的对应关系

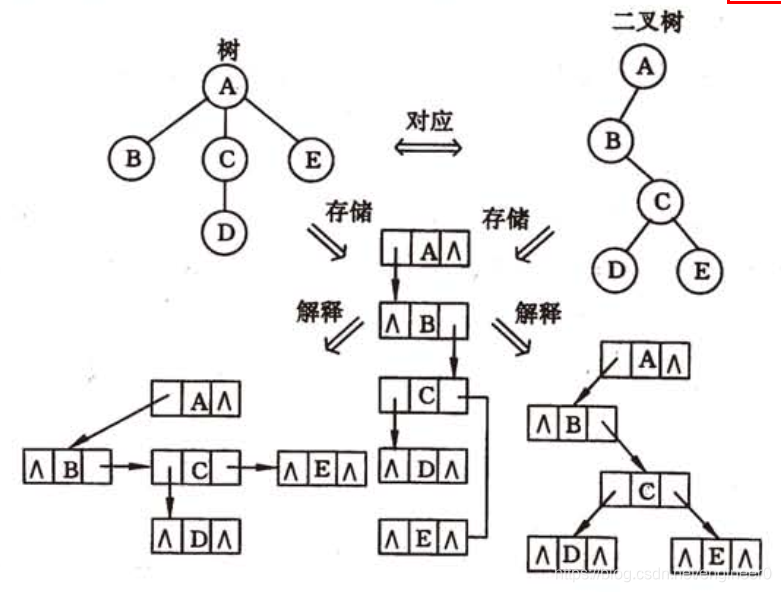
二叉树可以用二叉链表作为存储结构；
树也可以使用二叉链表作为存储结构。
一棵树和一个二叉树由此建立对应关系
如下，
任意一颗和树对应的二叉树，其右结点必定为空（因为树的根结点是没有兄弟结点的，其二叉链表根节点的右链域必为空）。

2、森林和二叉树的对应关系

方法：
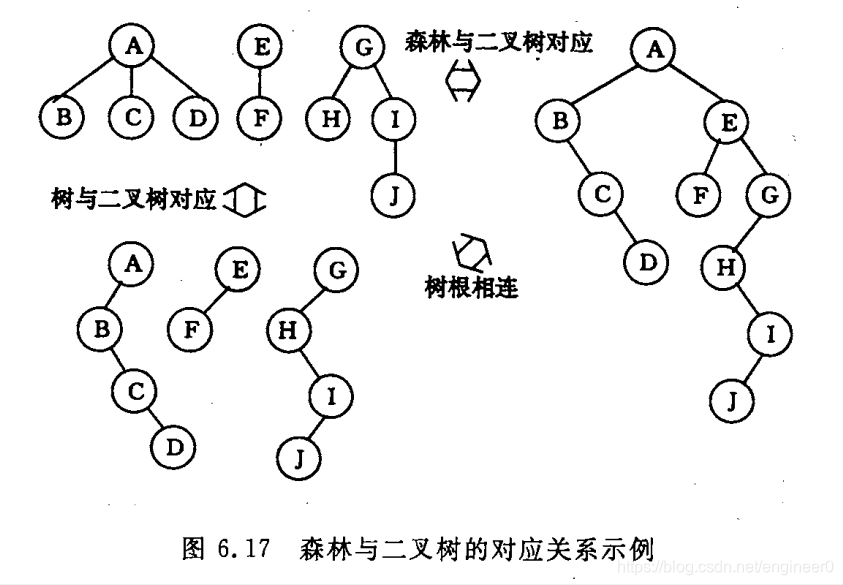
把森林中的第二棵树的根结点、第三棵树的根结点 … 都看作是第一棵树的根结点的兄弟结点。
因此顺着第一棵树的根结点右链域依次排下去
一个实例如下图

3、森林或数 <----> 二叉树（相互转化）

森林转换成二叉树（ F2B ）
已知森林 F = { T₁ , T₂ , … , T_m } ，B = { ROOT，LB，RB }
a. 若F为空，则m = 0 , B为空树。
b. 若F非空，则m不为0，B的根root即为F中 T₁ 的根结点 ROOT(T₁)；B的左子树 LB 是从 T₁ 根结点的子树森林F₁ = { T₁₁ , T₁₂ , … , T_1m } 转换而成的二叉树；B的右子树 RB 是从森林 F ^’ = { T₂ , T₃, … , T_m } 转换而成的二叉树。
二叉树转换成森林（ B2F ）
已知 B = { ROOT，LB，RB }，森林 F = { T₁ , T₂ , … , T_m }
a. 若 B 为空，那么 F 为空
b.若 B 非空，则 F 中第一棵树 T₁ 的根 ROOT(T₁) 即为二叉树 B 的根 root；T₁ 的子树森林 F₁ 是由 LB 转化而来；而 T₂，T₃，… ，T_m 组成的森林是由 RB 转换而来。