6.4.3 树和森林的遍历

1、前言

• 由于森林和树可以用二叉链表来表示，而二叉树也可以用二叉链表来表示。（最大区别在于每个结点和其右子树的关系）
  因此可以将一些森林和树的操作转换成二叉树的操作。

• 下面讲解树和森林的遍历和二叉链表的遍历的关系

2、树的遍历

• 有两种遍历树的方法 ( 递归 )
  1、先根遍历：先访问树的根结点，然后依次先根遍历根的每一颗子树
  2、后根遍历：先依次后根遍历每棵子树，然后访问根节点

示例

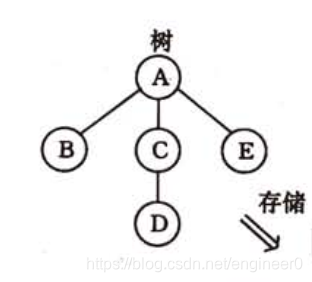
上面的树的先根遍历序列：A . B . C . D . E
上面的树的后根遍历序列：B . D . C . E . A

3、森林的遍历

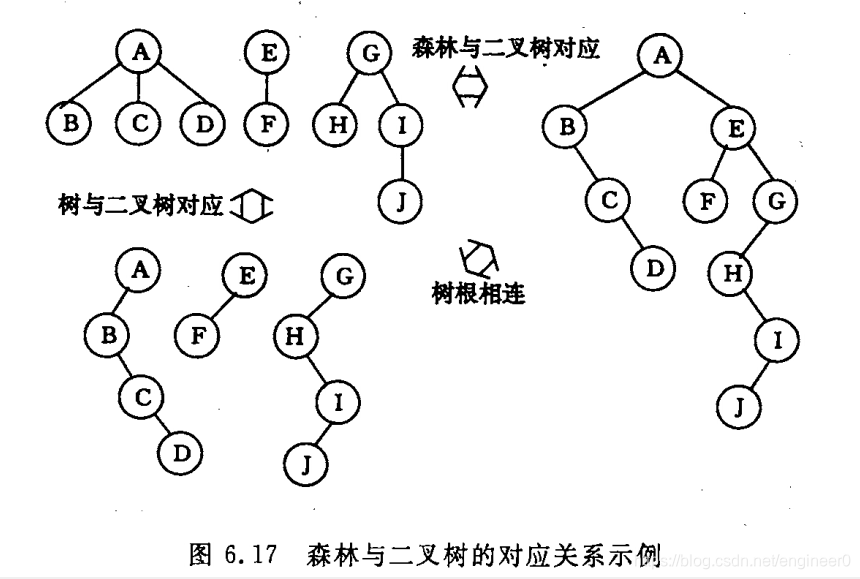
• 1、先序遍历森林（若森林非空）（同二叉链表的先序遍历）
  a. 访问森林中第一棵树的根结点
  b. 先序遍历第一棵树中根结点的子树森林
  c. 先序遍历除去第一棵树之后剩余的树构成的森林
  上图的先序遍历序列：A . B . C . D . E . F . G . H . I . J
森林的先序遍历 对应 二叉链表的先序遍历
• 2、后序遍历森林（若森林非空）(同二叉链表的中序遍历)
  只要记住从每个结点来看是后序的，即先后序访问完子树结点，再访问根结点即可。
  书上讲的比较乱，很难理解，又难以自圆其说。
  多分支树不存在中序遍历！比如一个结点有4个子树，那么中序遍历这个结点的树时，啥时候访问这个根结点？中序遍历只存在于二叉树 / 二叉链表中。
  森林后序遍历 对应 森林的二叉链表中序遍历
  上图的后序遍历序列：B . C . D . A . F . E . H . J . I . G

注意下列转换

树	森林	二叉树
先根	先序	先序
后根	中序	中序

4、应用：输出一棵树中所有 从根到叶子的路径 的算法

• 1、二叉树 / 二叉链表

void AllPath(BiTree T, Stack &S)
{
	if(T)
	{
		Push(S, T->data);
		if(!T->Left && !T->Right)
		{
			PrintStack(S);
		}
		else
		{
			AllPath(T->Left, S);
			AllPath(T->Right, S);
		}
		Pop(S);
	}
}

建议自己在纸上画出遍历时栈的动态过程（当然了，只是建议）。

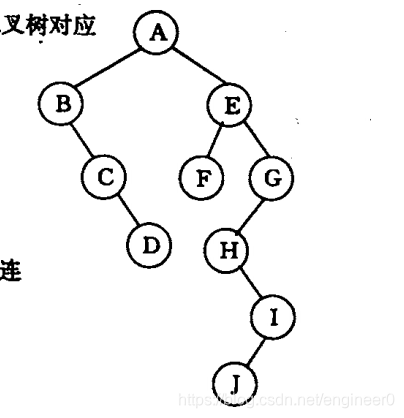
• 2、树的二叉链表求叶子结点
  那么二叉链表上没有左子树的结点就是叶子结点。
  在遍历树的二叉链表时，当顺着一个结点A的右子树进行遍历时，要先将A退栈，因为A的右子树结点B其实是A的兄弟结点，A 和 B 具有共同的根结点。因此在访问一个结点的右子树前务必要先将该结点退栈。

void OutPath(BiTree T, Stack &S)
{
	while(!T)
	{
		Push(S, T->data);
		if(!T->lchild)
		{
			PrintStack(S);
		}
		else
		{
			OutPath(T->lchild, S);
		}
		Pop(S);
		T = T->rchild; // 直到森林中每个根结点都遍历完，若T没变化，不能用while
	} //while
} // OutPath

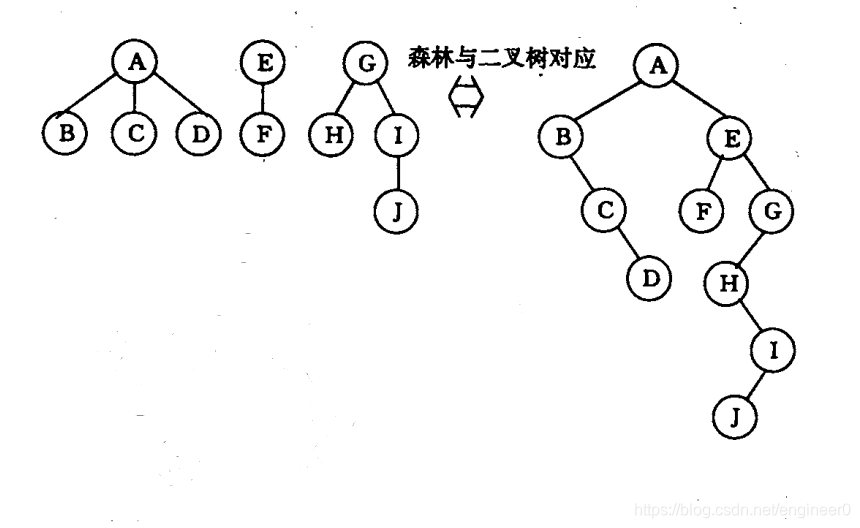
• 3、建立树的存储结构
  注意要按序输入，从上到下，从左到右

void CreatTree(CSTree &T)
{
	T = NULL;
	for(scanf(&fa, &ch);
			ch != '#';
			scanf(&fa, &ch) )
	{
		// 建立一个结点，父结点域为fa，数据域为ch
		// p 为结点指针，
		p = GetTreeNode(ch);
		// 将该结点指针入队列
		EnQueue(Q, p);
		if(fa == '#')
		{
			// fa域 为 '#' ，表示该结点无父母结点，就是根结点
			// 树T 就由 p来表示
			T = p;
		}
		else
		{
			// 不是根结点
			GetHead(Q, s);
			//找到刚创建的这个结点的父母结点
			while(s->data != fa)
			{
				DeQueue(Q, s); // 队列头出一个
				GetHead(Q, s); // 获取新的队列头
			}
			if(!(s->firstChild))
			{
				s->firstChild = p;
				r = p;
			}
			else
			{
				r->nextSibling = p;
				r = p;
			}
		}
	}
}