6.3.2 线索二叉树_双向链表储存对二叉树的遍历-优快云博客

引入的原因

遍历二叉树的结果是求得结点的一个线性序列。对非线性结构进行线性化操作。
当以二叉链表作为存储结构时，只能找到结点的左右孩子信息，而不能直接得到结点在任一序列中的前驱和后继信息，这种信息只有在遍历的动态过程中才能得到。
先序、中序和后序遍历过程中，各个结点的前驱和后继一般是不同的。
对线索二叉树进行遍历时就不再需要栈，也不再需要递归了。（优越性）

线索二叉树的定义

有 n 个结点的二叉链表，必定存在 n+1 个空链域，可以利用这些空链域来存放结点的前驱和后继信息。
规定：
若节点有左子树，则其 lchild 域指示其左孩子，否则令 lchild 域指示其前驱。
若节点有右子树，则其 rchild 域指示其右孩子，否则令 rchild 域指示其后继。
为了区分左子树和前驱，右子树和后继：增设两个标志域。
LTag 为0表示结点的左孩子，为1表示结点的前驱。
RTag 为0表示结点的右孩子，为1表示结点的后继。
一般只在叶子结点和附加的头结点进行线索化。就是向原本是空链域的地方加上线索（前驱 / 后继）
线索链表：以上图这种结构构成的二叉链表作为二叉树的存储结构，( 包含线索 ) 叫做线索链表。
线索：结点的前驱指针和结点的后继指针。
线索化：对二叉树以某种次序遍历使其变为线索二叉树的过程叫做线索化。

线索二叉树的性质

由于线索是通过遍历二叉树得到的，而先、中、后序的遍历顺序不一样，因此先序、中序、后序的线索必然不同。
线索化的二叉树实在二叉树的基础上构成的，线索化不是每个结点都加上线索。
所有的前驱指针都加在左子树域为空的结点上；有左子树就指向左子树的根结点，否则指向前驱。
所有的后继指针都加在右子树域为空的结点上。有右子树就指向右子树的根结点，否则指向后继。
n个结点的二叉树必定有n+1个空链域。因此必有n+1个线索。
一般为二叉链表附设一个头结点。（以中序为例）
若是空二叉树，该头结点的左右链域均回指。
若二叉树不空，让头结点的左链域指向根结点，右指针指向末访结点；
让二叉树的首访结点的前驱指向头结点，让二叉树的末访结点的后继指向头结点。
如上建立一个双向循环链表。可以从第一个结点顺后继进行遍历，也可以从最后一个结点顺前驱进行遍历。
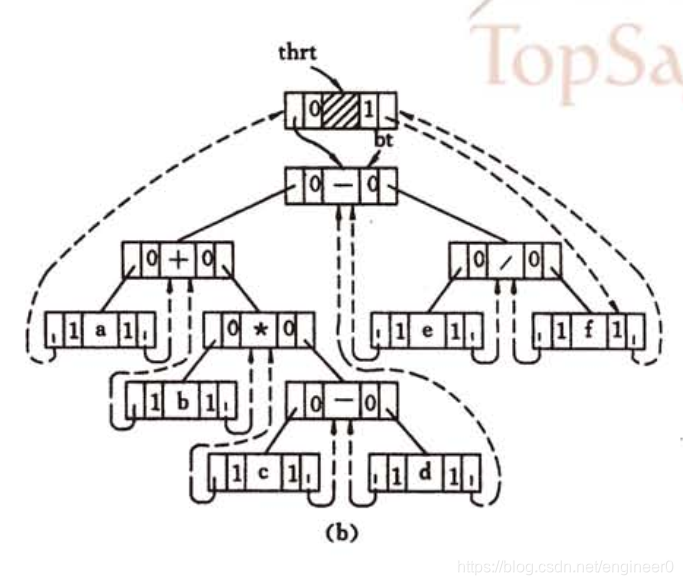
一个中序线索链表示例：
虚线表示线索，指示当前结点的前驱、后继。
实线表示指针，指示当前结点的左、右子树的根结点。

在这里插入图片描述

线索链表遍历的代码实现（以中序为例！！）

基本思想

从首访结点开始找后继，直到后继为空即可。能找到每个结点正确的后继就行！

结点的后继：该结点的后继是遍历其右子树时访问的第一个结点，即右子树最左下的点。没有右子树就依据后继线索。
结点的前驱：该结点的前驱是遍历其左子树时访问的最后一个结点，即左子树最右下的点。没有左子树就依据前驱线索。

for(p = firstNode(T); p; p = Next(p) )
{
	// firstNode 表示首元结点
	// Next 表示后继结点
	Visit(p);
}

二叉树的二叉线索存储表示

typedef enum PointerTag
{
	Link,	// Link == 0, 指针，指向左右孩子
	Thread	// Thread == 1, 线索，指向前驱 / 后继
};

typedef struct BiThrNode
{
	TElemType data;
	struct BiThrNode *lchild, *rchild;	// 左右孩子指针 / 线索
	PointerTag LTag, RTag;				// 左右标志
} BiThrNode, *BiThrTree;

以双向链表作为存储结构对二叉树进行遍历

相比普通二叉链表遍历的优越性：不需要栈，不需要递归。

Status InOrderTraverse_Thr(BiThrTree T, Status (*visit)(TElemType e))
{
	// T指向头结点，T的左链lchild指向根结点，右链指向中序最后一个结点
	// 中序遍历
	// T指向头结点，p指向根结点
	p = T->lchild;
	// 空树或者遍历结束时，P == T
	while(p != T)
	{
		while(p->LTag == LINK)
		{
			p = p->lchild;
		}
		if(!visit(p->data))
		{
			return ERROR;
		}
		// 当 p 没有右子树 且 不是最后一个结点时
		// 确保接下来 p 能转化为自己的后继                                                                                                                                                                   
		while(p->RTag == Thread && p->rchild != T)
		{
			p = p->rchild;
			visit(p->data);
		}
		p = p->rchild;
	}
	return OK;
}

二叉树的线索化
实质：将二叉树中的空指针改为指向前驱或者后继的线索，而前驱和后继的信息只有在遍历时才能得到，因此线索化的过程即为在遍历的过程中修改空指针的过程。
需要附设一个指针 pre 始终指向刚刚访问过的结点。

// 中序遍历二叉树T，并将其中序线索化
// Thrt为头结点，T为根结点
Status InOrderThreading(BiThrTree Thrt, BiThrTree T)
{
	// 加入头结点
	if(!(Thrt = (BiThrTree)malloc(sizeof(BiThrNode))))
	{
		exit(OVERFLOW);
	}
	// 左标志必为 link
	// 右标志 必为 Thread
	Thrt->LTag = Link;
	Thrt->Rtag = Thread;
	// 头结点右指针回指
	Thrt->rchild = Thrt;
	if(!T)
	{
		// T为空树，则头结点的左指针回指
		Thrt->ltag = Thread;
		Thrt->lchild = Thrt;
	}
	else
	{
		Thrt->lchild = T;
		pre = Thrt;
		// 递归实现线索化
		InThreading(T);
		// 对线索化过程中最后一个结点进行处理
		pre->rchild = Thrt;
		pre->RTag = Thread;
		Thrt->rchild = pre;
	}
	return OK;                                                                                                                                                                                                                                                                                                                                                                        
}

void InThreading(BiThrTree p)
{
	// 只有在访问结点的时候
	// 才能进行线性化操作。
	if(p)
	{
		// 对该结点的左子树进行线索化（递归）
		InThreading(p->lchild);
		// 对当前结点进行线索化
		if(!p->lchild)
		{
			p->LTag = Thread;
			p->lchild = pre;
		}
		// 对当前结点的前驱进行线索化
		if(!pre->rchild)
		{
			pre->RTag = Thread;
			pre ->rchild = p;
		}
		// 一旦访问了某个结点，
		// 访问完毕 当前结点 立刻变成 pre。
		pre = p;
		InThreading(p->rchild);
	}
}