卡特兰数
1. 定义与背景
卡塔兰数是组合数学中一个常出现在各种计数问题中出现的数列。由以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。
卡塔兰数的一般项公式为 
另类递归式 $ h(n)=\frac{4*n-2}{n+1}*h(n-1)$
前几项为: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …
2. 性质
* C n C_n Cn*的另一个表达形式为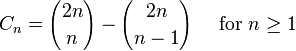 所以,C**n是一个自然数;这一点在先前的通项公式中并不显而易见。这个表达形式也是André对前一公式证明的基础。(见下文的第二个证明。)
所以,C**n是一个自然数;这一点在先前的通项公式中并不显而易见。这个表达形式也是André对前一公式证明的基础。(见下文的第二个证明。)
卡塔兰数满足以下递推关系

它也满足

这提供了一个更快速的方法来计算卡塔兰数。
卡塔兰数的渐近增长为
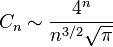
它的含义是左式除以右式的商趋向于1当n → ∞。(这可以用n!的斯特灵公式来证明。)
所有的奇卡塔兰数C_{n}都满足n = 2k − 1。所有其他的卡塔兰数都是偶数。
递推公式

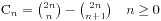
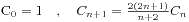
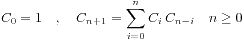
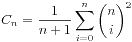
3.应用
- C n C_{n} Cn 表示长度2n的dyck word的个数。Dyck word是一个有n个X和n个Y组成的字串,且所有的部分字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY
- 将上例的X换成左括号,Y换成右括号,C**n表示所有包含n组括号的合法运算式的个数:
((())) ()(()) ()()() (())() (()())
C n C_{n} Cn表示有n+1个叶子的二叉树的个数。

- C n C_{n}





 本文详细介绍了卡特兰数的定义、性质、应用,并提供了编程求解第n个卡特兰数的方法。卡特兰数在组合数学中广泛出现,与括号表达式、二叉树、 Dyck 字符串等多个领域有密切联系。同时,文章给出了计算卡特兰数的递推公式,并探讨了其在剧场购票问题中的应用。
本文详细介绍了卡特兰数的定义、性质、应用,并提供了编程求解第n个卡特兰数的方法。卡特兰数在组合数学中广泛出现,与括号表达式、二叉树、 Dyck 字符串等多个领域有密切联系。同时,文章给出了计算卡特兰数的递推公式,并探讨了其在剧场购票问题中的应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1611
1611

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








