CMOS参考电流生成方法

互补金属氧化物半导体中精确的参考电流生成方法和电路

E. Mkrtchyan, V. Melikyan,
新思科技亚美尼亚有限公司 新思技亚美尼亚有限公司
A. Martirosyan， D. Babayan，
新思科技亚美尼亚有限公司 新思科技亚美尼亚有限公司

已评估硅的特性。作为第二个参考，选择了金属氧化物半导体（MOS）晶体管的栅极氧化层厚度。
在线性工作区，MOS晶体管的漏极电流与栅源电压的关系如下
$$ I_D = \beta(V_{GS} - V_T)V_{DS} - \frac{1}{2}\beta V_{DS}^2 $$, (1)
其中 $$ \beta = \mu C_{ox}(W/L) $$ (2)
通过尺寸调节，晶体管的线性尺寸（W，L）在工艺和温度（PT）下的变化可以保持非常小。$$ \Delta(W/L) $$ 对PT的依赖性可忽略不计。氧化层厚度 $$ t_{ox} $$ 在PT下的变化小于4.5%。公式（1）中温度相关参数（与工艺变化无关）影响最大的是载流子迁移率 $$ \mu $$。因此，公式（1）中固定温度下 $$ \beta $$ 的整体变化由 $$ \mu $$ 决定（~5%）。

考虑两个尺寸相同的在线性（三极管区）工作的 NMOS晶体管，其漏极电流之差，这两个晶体管具有不同的栅源电压1、栅源电压2和漏源电压1=Vds2（图 1）。根据(1)，MN1、MN2（图1）的漏极电流差为
$$ \Delta I = \beta(V_{GS1} - V_{GS2})V_{DS} $$ (3)
公式(3)中的所有电压均可参考带隙电压基准发生器，且在工艺、温度和电源电压（PVT）范围内具有大约 ±5% 的变化。根据公式(3)，理想情况下对 $$ \beta $$ 的温度依赖性进行补偿，将使 ±5%的变化率与 $$ \Delta I $$ 保持一致。

$$ \beta $$ 随温度的一阶依赖关系由以下方程决定
$$ \mu(T) = \mu_0(T/T_0)^{-\gamma} $$ (4)
$$ \beta(T) = \beta_0(T/T_0)^{-\gamma} $$ (5)
接下来假设将与绝对温度成正比的电压（PTAT）施加到公式（1）中的 $$ V_{DS} $$，且 $$ V_{GS1} - V_{GS2} $$ 等于 $$ V_{const} $$，其中 $$ V_{const} $$ 是与温度无关的电压。相应地，公式（1）可写为
$$ I_{D1} = \beta(V_{GS1} - V_T)V_{PTAT} - \frac{1}{2}\beta V_{PTAT}^2 $$ (6)
$$ I_{D2} = \beta(V_{GS2} - V_T)V_{PTAT} - \frac{1}{2}\beta V_{PTAT}^2 $$ (7)
其中 $$ V_{PTAT} $$ 是PTAT电压。经过上述变换后，$$ \Delta I $$ 的温度依赖性如下
$$ \Delta I = \alpha \beta V_{const} V_{PTAT} $$ (8)
其中 $$ \alpha $$ 是 $$ V_{PTAT} $$ 的温度系数。

为了在 $$ T_0 $$ 附近获得温度补偿，应将公式（8）的导数设为0，并求解 $$ V_{const} $$。
$$ \left. \frac{d(\Delta I)}{dT} \right| {T=T_0} = 0 $$ (9)
从中可得
$$ V {const} = \frac{kT_0}{q} \cdot \frac{1}{\alpha} $$, 其中 $$ k $$ 是玻尔兹曼常数，$$ q $$ 是电子电荷 (10)
根据(9)，通过为 $$ V_{const} $$ 选择适当的值（(9)中的 $$ \alpha $$ 是PTAT电压 $$ V_{PTAT} $$ 的温度系数），可以获得所需的 $$ T_0 $$ 温度，在该温度附近电流将保持平坦。因此，通过改变 $$ V_{const} $$，可以在任意期望的 $$ T_0 $$ 周围实现平坦的曲线。

3. 提出的电路

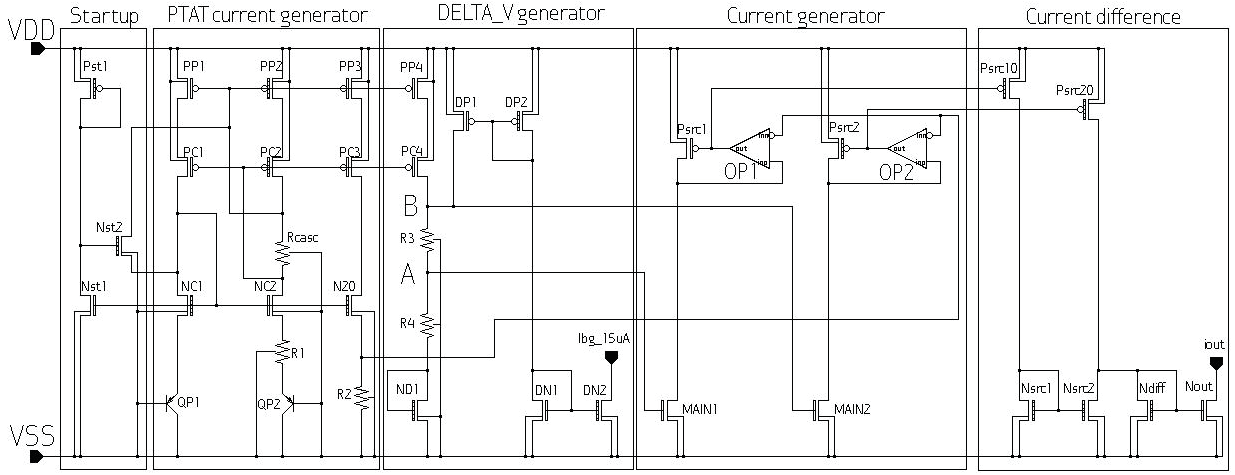
所提出的电路的实现基于两个尺寸相同的在线性区工作的NMOS晶体管（图1中的main1、main2），它们由不同的栅源电压驱动。通过Op1和Op2运算放大器，将一个与绝对温度成正比的相同电压施加到 NMOS晶体管的漏极。该电压由一个与绝对温度成正比的电流源和电阻R2（图1）产生，并施加到 Op1和Op2的参考输入端。同一个（或成倍的）与绝对温度成正比的电流通过PP4晶体管镜像，并施加到 M01、R3、R4串联支路。通过将15uA（ibg_15uA）带隙基准电流镜像到同一M01、R3、R4支路，生成一个与温度无关的电压 $$ V_{const} $$（在工艺、电压、温度（PVT）范围内变化为±5%）。流过M01、R3、 R4的总电流是带隙提供的与温度无关的电流和从与绝对温度成正比的电流源镜像而来的PTAT电流之和。

在A点和C点产生的电压差决定了main1和main2器件的工作区域。该电压差应确保所述器件在整个 PVT范围内的线性工作。A点获得的电压等于 $$ V_{PTAT} $$，并驱动栅极

main1的长度。B点的电压等于 $$ V_{PTAT} + V_{const} $$，并施加到n型主晶体管2的栅极上。$$ V_{const} $$ 用于提供驱动main1和main2所需的电压偏移。

由 $$ V_{const} $$ 引入的工艺、电压、温度（PVT）变化对main1和main2晶体管产生的电流影响相同，因此在电流差（图1）电路中，当这两个晶体管产生的电流相减时，该影响被抵消。运算放大器Op1和Op2在P型源极晶体管1和P型源极晶体管2的栅极上设置的电压，分别由流过main1和main2晶体管的电流决定。因此，P型源极晶体管10镜像了main1产生的电流，P型源极晶体管20镜像了main2产生的电流。电流差遵循公式 (6)，从而在给定的 $$ V_{const} $$ 下实现PVT补偿。$$ V_{const} $$ 的值由绝对电流（ibg_15微安）设定。图1中输出电流iout在工艺、电压、温度（PVT）变化下的波动为~±12%。

4. 实验结果

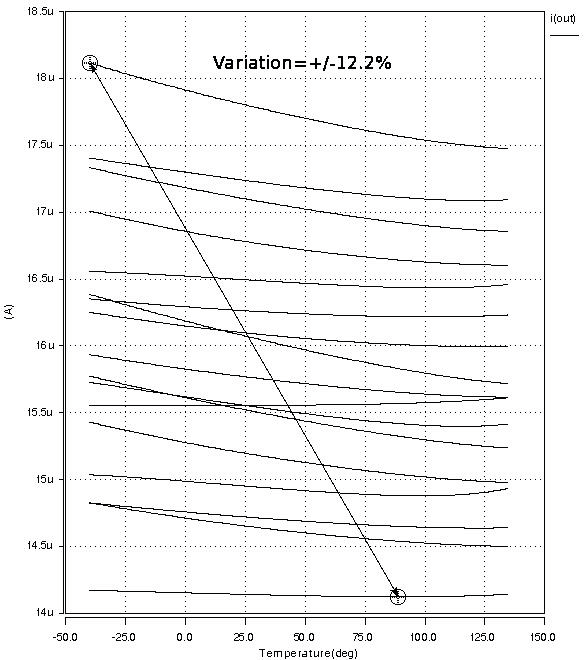
所提出的电路已在28纳米1.8伏CMOS工艺中设计，并通过HSpice仿真器建模。图2显示了PVT变化下的仿真结果。仿真中考虑了片上多晶硅电阻、MOS器件、双极型晶体管以及电源电压和温度的变化。如图所示，在‐40°C至125°C的温度范围内，输出电流的PVT变化为±12.2%。

5. 结论

本文提出了一种设计高精度参考电流电路的方法。基于该方法设计了电流发生器电路，并使用HSpice进行了仿真。为了补偿工艺变化，电路采用了两个工作在三极管区的NMOS晶体管。温度变化通过利用具有不同温度依赖特性的电流差值进行补偿。仿真结果显示，在工艺角和‐40°C至125°C温度范围内，输出电流的变化为±12.2%。