论文信息
Tsung-Yi Lin, Priya Goyal, Ross Girshick, Kaiming He, Piotr Dollár, Focal Loss for Dense Object Detection, ICCV 2017.
https://arxiv.org/abs/1708.02002
历史的发展
我们重点关注神经网络重新崛起之后的内容, 先前的内容以后也许会简单提一下.
两大门派
两大门派主要是one stage与two stage, 二者在accuracy与speed各有侧重, 但最终还是trade-off.
| one stage | two stage | |
|---|---|---|
| algorithms | YOLO, YOLT | R-CNN, SPPnet |
| accuracy | Low(30% mAP) | High(60%+ mAP) |
| speed | Fast(100+ FPS) | Slow(5 FPS) |
two stage
其主要特点是先使用某种算法(selective search, RPN, etc.)产生一系列proposal, 将这些proposal喂到某个预训练神经网络(VGG-16, ResNet, etc.)中, 之后对输出进行分类.
特别的, RPN会预分类(background vs foreground)
one stage
大多数模型会采用一系列类似于滑窗分类器或是"anchor"直接进行分类而无proposal过程.
RetinaNet
本文中的模型是基于one stage, 目的也显而易见便是为了提升accuracy.
主要贡献
提出观点: 导致one stage精确度不足的重要原因有class imbalance.
class imbalance
所谓class imbalance便是由于two stage模型大多会对bg与fg预分类, 因此bg数量不会远大于fg数量, 而one stage模型为了提升速度舍弃了proposal过程, 因此大多数模型也谈不上预分类问题,这样虽然速度提升并且使用交叉熵, 但往往还是由于easy sample(e.g. bg)远大于hard sample(e.g. fg), 往往相差2 order, 以至于easy sample的loss统治整体loss.
此前的一些解决方案
OHEM直接舍弃部分easy example, 毫无疑问会导致数据残缺, 进而影响结果
本文的解决方案
提出了一个新的loss func:
C
E
(
p
t
)
=
−
l
o
g
(
p
t
)
F
L
(
p
t
)
=
−
α
t
(
1
−
p
t
)
γ
C
E
(
p
t
)
CE(p_t) = -log(p_t)\\ FL(p_t) = -\alpha_t(1-p_t)^\gamma CE(p_t)
CE(pt)=−log(pt)FL(pt)=−αt(1−pt)γCE(pt)
其中
p
t
=
{
p
y
=
1
1
−
p
o
t
h
e
r
w
i
s
e
α
t
=
{
α
y
=
1
1
−
α
o
t
h
e
r
w
i
s
e
p_t=\left\{ \begin{aligned} p && y = 1\\ 1-p && otherwise \end{aligned} \right.\\ \alpha_t=\left\{ \begin{aligned} \alpha && y = 1\\ 1-\alpha && otherwise \end{aligned} \right.
pt={p1−py=1otherwiseαt={α1−αy=1otherwise
特别的,
C
E
CE
CE是交叉熵. 在作者的实验中发现
γ
=
2
,
α
=
0.25
\gamma = 2, \alpha = 0.25
γ=2,α=0.25时取得最好结果.
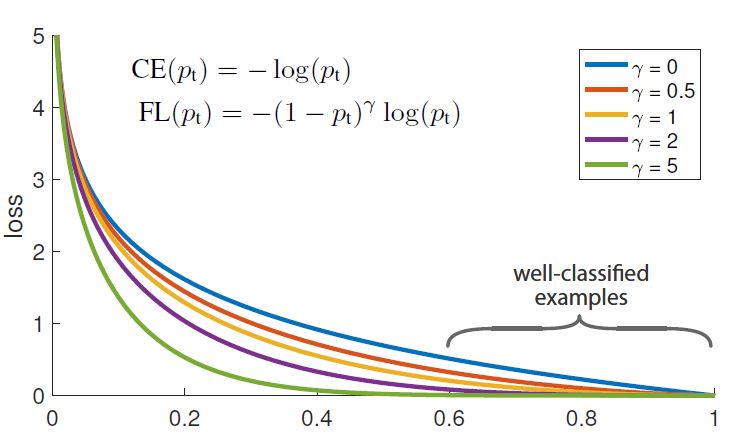
通过仿真图我们可以发现, 对于相对有把握的类别(easy sample, e.g. bg), loss设置较小, 而对于较没有把握的类别(hard sample, e.g. fg), loss较大, 这样就防止出现把握较大的类别因为数量优势统治loss.
我们从四种情况分析loss函数:
-
正确分类 & 目标项容易分类 - y = 1 , p ≈ 1 y = 1, p \approx 1 y=1,p≈1
此时 p t = p ≈ 1 p_t = p \approx 1 pt=p≈1, 而 γ > 1 \gamma > 1 γ>1, 因此 F L ( p t ) < < C E ( p t ) FL(p_t) << CE(p_t) FL(pt)<<CE(pt)
-
正确分类 & 目标项不易分类 - y = 1 , p ≈ 0 y = 1, p \approx 0 y=1,p≈0
此时 p t = p ≈ 0 p_t = p \approx 0 pt=p≈0, 而 γ > 1 \gamma > 1 γ>1, 因此 F L ( p t ) ≈ C E ( p t ) FL(p_t) \approx CE(p_t) FL(pt)≈CE(pt)
-
错误分类 & 目标项容易分类 - y = − 1 , p ≈ 1 y = -1, p \approx 1 y=−1,p≈1
此时 p t = 1 − p ≈ 0 p_t = 1 - p \approx 0 pt=1−p≈0, 而 γ > 1 \gamma > 1 γ>1, 因此 F L ( p t ) ≈ C E ( p t ) FL(p_t) \approx CE(p_t) FL(pt)≈CE(pt)
-
错误分类 & 目标项不易分类 - y = − 1 , p ≈ 0 y = -1, p \approx 0 y=−1,p≈0
此时 p t = 1 − p ≈ 1 p_t = 1 - p \approx 1 pt=1−p≈1, 而 γ > 1 \gamma > 1 γ>1, 因此 F L ( p t ) < < C E ( p t ) FL(p_t) << CE(p_t) FL(pt)<<CE(pt)
以一言蔽之, 易分类未出错的影响大量减小.
特别的, 易分类出错影响基本不减小也很合理.
额外的 - 网络构建
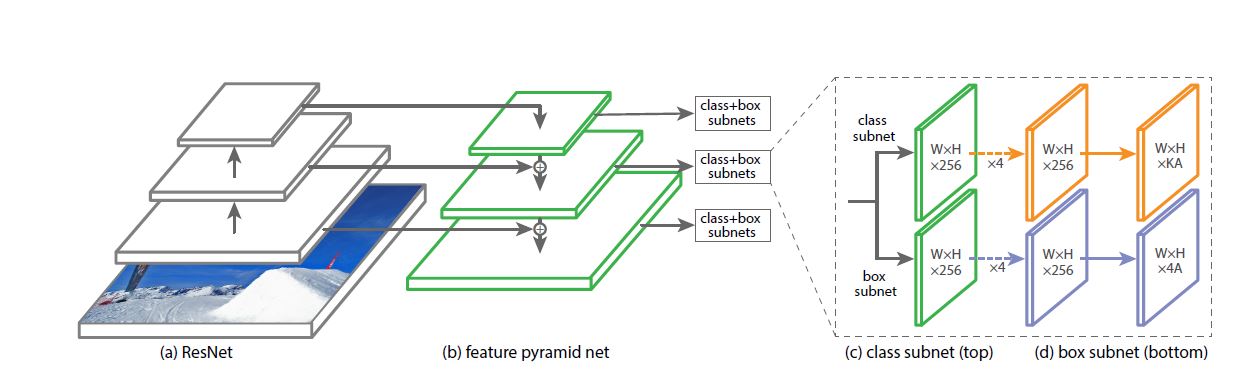
该网络很容易看出左半部分就是FPN, 而对于右半部分就是他们独创的, 很容易看出(论文中也提到了)他们分了上下两个parameter not shared卷积网络, 一个是用来classifying另一个是用来anchor box regressing(4 dims).
Initialization
Bias initialization for classification subnet:
b
=
−
l
o
g
(
1
−
π
/
π
)
b = -log(1 - \pi/\pi)
b=−log(1−π/π)
π
\pi
π是指所有初始化时所有anchor都有
π
\pi
π的把握被当作fg, 实践证明
π
=
0.01
\pi = 0.01
π=0.01较为合适.
实验结果
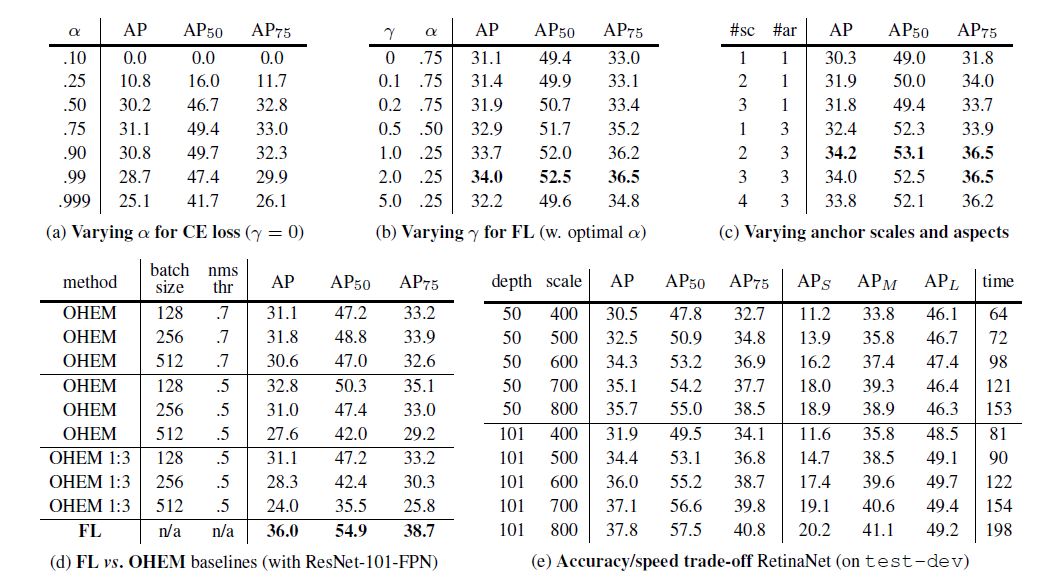
这里要补充的时OHEM 1 : 3指舍弃low probability后fg : bg.
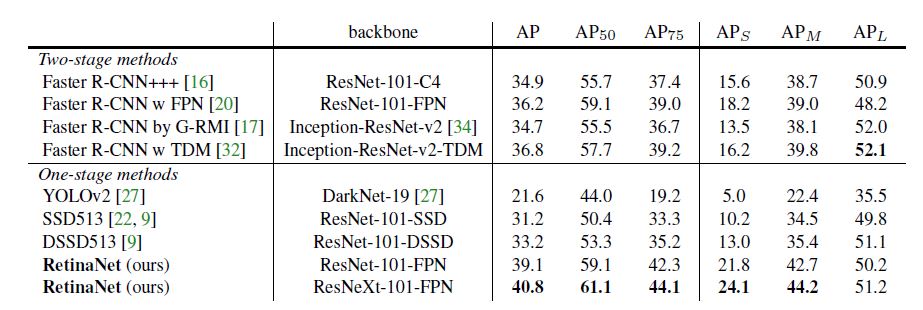
这张图的结果来看, RetinaNet也可以称得上名副其实的state-of-the-art.
Appendix
A
首先定义了:
x
t
=
y
x
,
y
∈
{
±
1
}
x_t = yx, y\in\{\pm1\}
xt=yx,y∈{±1}
其中
x
x
x表示数量.
尝试了一个Focal Loss的变体, 得出的结论用原文总结就是:
More generally, we expect any loss function with similar properties as FL or FL* to be equally effective.
B
d C E d x = y ( p t − 1 ) F L d x = y ( 1 − p t ) γ ( γ p t l o g ( p t ) + p t − 1 ) d F L ∗ d x = y ( p t ∗ − 1 ) \frac{dCE}{dx} = y(p_t - 1)\\ \frac{FL}{dx} = y(1 - p_t)^\gamma(\gamma p_t log(p_t) + p_t - 1)\\ \frac{dFL^*}{dx} = y(p_t^* - 1) dxdCE=y(pt−1)dxFL=y(1−pt)γ(γptlog(pt)+pt−1)dxdFL∗=y(pt∗−1)
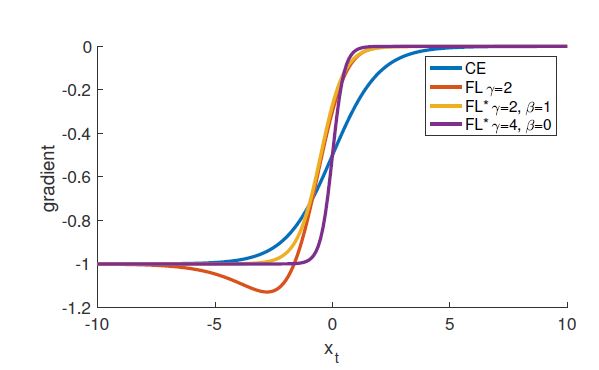
得出结论, 当 x t > 0 x_t > 0 xt>0时, FL导数比CE更接近于零.
总结
要善于发现问题的本质 - 从当时流行的方法中看one stage algorithms比不上two stage algorithms的一个重要原因.




















 621
621

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








