【深度强化学习笔记】--第二节：马尔可夫决策过程

最新推荐文章于 2025-03-21 08:05:29 发布
原创 最新推荐文章于 2025-03-21 08:05:29 发布 · 369 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#强化学习

本文深入解析了马尔可夫决策过程(MDP)的基本构造，包括状态、动作、状态转移概率、奖励函数及策略函数，强调了其马尔可夫性质，并介绍了折扣因子如何影响决策策略。同时，给出了MDP的五元组形式(S,A,P(a|s),R(s|a),γ)。

1.马尔可夫性质

马尔可夫决策过程（Markov Decision Process, MDP）独有性质即当前时刻的状态仅与前一时刻的状态和动作有关，与其他时刻的状态和动作条件独立。
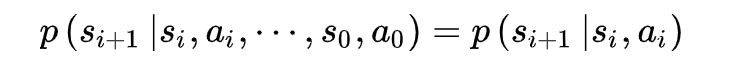
在这里插入图片描述
等式右侧的条件概率被称为MDP的状态间的转移概率 。马尔可夫性质是所有马尔可夫模型共有的性质，但相比于马尔可夫链，MDP的转移概率加入了智能体的动作，其马尔可夫性质也与动作有关

2.MDP基本组成部分

状态集合
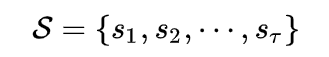
在这里插入图片描述
动作集合
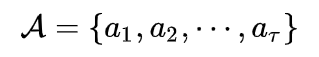
在这里插入图片描述
状态转移概率函数
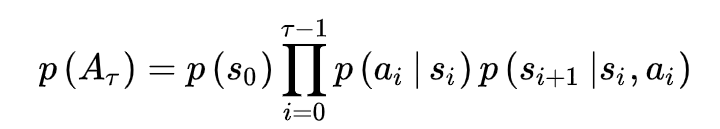
在这里插入图片描述
奖励函数
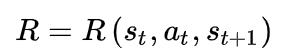
在这里插入图片描述
策略函数
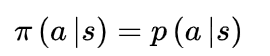
在这里插入图片描述
●折扣因子:γ∈[0,1]
◆γ=0:贪婪法,价值只由当前延时奖励决定;
◆γ=1:所有后续状态奖励和当前状态奖励同等重要;
◆γ∈(0,1):当前延时奖励的权重比后续奖励的权重大。
马尔科夫决策过程可以表示成一个五元组

MDP(S,A,P(a|s),R(s|a),γ)

强化学习从基础到进阶-案例与实践[2]：马尔科夫决策、贝尔曼方程、动态规划、策略价值迭代
丨汀、的博客
06-20 2084
【强化学习原理+项目专栏】必看系列：单智能体、多智能体算法原理+项目实战、相关技巧（调参、画图等、趣味项目实现、学术应用项目实现 专栏详细介绍：【强化学习原理+项目专栏】必看系列：单智能体、多智能体算法原理+项目实战、相关技巧（调参、画图等、趣味项目实现、学术应用项目实现对于深度强化学习这块规划为：本专栏主要方便入门同学快速掌握强化学习单智能体|多智能体算法原理+项目实战。后续会持续把深度学习涉及知识原理分析给大家，让大家在项目实操的同时也能知识储备，知其然、知其所以然、知何由以知其所以然。声明：部分项目为
【深度学习】强化学习（二）马尔可夫决策过程
2401_86518761的博客
08-08 1384
在给西瓜浇水的马尔可夫决策过程中，只有四个状态（健康、缺水、溢水、凋亡）和两个动作（浇水、不浇水），在每一 步转移后,若状态是保持瓜苗健康则获得奖赏1 ,瓜苗缺水或溢水奖赏为- 1 , 这时通过浇水或不浇水可以恢复健康状态，当瓜苗凋亡时奖赏是最小值-100 且无法恢复。分别表示导致状态转移的动作、转移概率以及返回的奖赏.容易看出，最优策略在“健康”状态选择动作 “浇水”、在 “溢水”状态选择动作“不浇水”、在 “缺水”状态选择动作 “浇水”、在 “凋亡”状态可选择任意动作。后，环境反馈给智能体的即时奖励。
马尔科夫链（Markov Chain）
大龄小白爱折腾的博客
10-27 9693
马尔科夫链原理简介
马尔可夫链在 A 股市场的量化应用(2)
最新发布
海哥谈量化
03-21 1358
昨天的小文抛砖引玉,昨晚又完善了一下,分析下马尔科夫链的相关公式与基础逻辑,看来可以融入到我的量化机器人了.#
马尔可夫性的统计检验（马氏性检验）
Fo*(Bi)的博客
08-17 1万+
马尔可夫预测法认为，只要当事物的现在状态为已知时，人们就可以预测其未来的状态，而不需要知道事物的过去状态，即马尔可夫链具有无后效性特征，这也被后人称为马尔可夫性。这一特性避开了其他预测方法在搜集历史资料时所遇到的一系列难题，使得它无论是理论上还是应用上都占有很重要的地位。 因此，检验随机过程是否具有马尔可夫性是应用马尔可夫概型分析的必要前提。 ...
深度强化学习入门：马尔可夫决策过程（井字棋案例理解）
God-Excious的博客
08-16 3092
以井字棋案例，讲解自己对于马尔可夫决策过程（MDP）的理解
强化学习笔记------第二章----马尔可夫决策过程（MDP）（超详细）
w18165269429的博客
03-31 2217
在介绍马尔可夫决策过程之前，先介绍它的简化版本：马尔可夫链以及马尔可夫奖励过程，通过跟这两种过程的比较，我们可以更容易理解马尔可夫决策过程。 Markov Process(MP) Markov Property 如果一个状态转移是符合马尔可夫的，那就是说下一个状态只取决于他当前状态，而跟他当前状态之前的状态都没有关系。 假定状态历史为ht={s1,s2,…,st}(ht包含了之前的所有状态)，如果一个状态转移是符合马尔科夫的，也就是满足如下条件： 从当前st转移到st+1这个状态，他就直接等于它之前所有的
马尔可夫决策过程-强化学习学习笔记(二)
优快云XXCQ的博客
01-19 4506
概念引入 强化学习的通俗理解 马尔可夫的通俗介绍 简介 马尔可夫决策过程 (Markov Decision Processes, MDPs)是对强化学习问题的数学描述. 马尔可夫决策过程（Markov Decision Process, MDP）是序贯决策（sequential decision）的数学模型，用于在系统状态具有马尔可夫性质的环境中模拟智能体可实现的随机性策略与回报 。MDP的得名来自于俄国数学家安德雷·马尔可夫（Андрей Андреевич Марков），以纪念其为马尔可夫链所做的研
强化学习自学指南：马尔可夫决策过程详解
在给定文件信息中，我们能够提取出有关强化学习和马尔可夫决策过程（Markov Decision Processes，MDP）的关键知识点。 首先，标题"Markov-decision-processes"直接指向了一个核心概念——马尔可夫决策过程。在强化...
OR（odd ratios）
likelet的专栏
03-20 1万+
OR值的全称是odd ratio, OR值是相对危险度，又称比值比，对于发病率很低的疾病来说，它是OR值即是相对危险度的精确估计值。 计算公式如下： Odd ratio, 95% CI 假定我们要鉴别一个基因（或者标记位点SNP）有两个等位基因（等位）:记为 Allele 1 Allele 2 Allele 1
x2检验（chi-square test）或称卡方检验
weixin_34342207的博客
10-25 6153
x2检验（chi-square test）或称卡方检验     x2检验（chi-square test）或称卡方检验，是一种用途较广的假设检验方法。可以分为成组比较（不配对资料）和个别比较（配对，或同一对象两种处理的比较）两类。     一、四格表资料的x2检验     例20.7某医院分别用化学疗法和化疗结合放射治疗卵巢癌肿患者，结果如表20-11，问两种疗法有无差别？ 表20-11 ...
T检验、F检验和统计学意义（P值或sig值）
lincy100的专栏
02-14 6160
1.T检验和F检验的由来 一般而言，为了确定从样本(sample)统计结果推论至总体时所犯错的概率，我们会利用统计学家所开发的一些统计方法，进行统计检定。 通过把所得到的统计检定值，与统计学家建立了一些随机变量的概率分布(probability distribution)进行比较，我们可以知道在多少%的机会下会得到目前的结果。倘若经比较后发现，出现这结果的机率很少，亦即是说，是在机会很少、很罕
精通Excel数据统计与分析 - 摘要 （第9章：马尔科夫链分析）
youngmiffy的博客
12-20 3880
一、马尔科夫链分析 9.1 马尔科夫链简介 马尔可夫性：系统在各个时期所处的状态是随机的，从这个时期到下个时期的状态按照一定的概率进行转移，且下个时期的状态只取决于这个时期的状态和转移概率，与之前各个时期的状态无关，这种性质称之为无后效性或马尔可夫性。 简单的马尔科夫链，利用Excel的矩阵乘法函数，或者使用规划纠结工具求解，复杂时可使用VBA编辑器编写程序。
卡方检验
Chain的博客
10-06 5397
什么是卡方检验 卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴，主要是比较两个及两个以上样本率( 构成比）以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。 它在分类资料统计推断中的应用，包括：两个率或两个构成比比较的卡方检验；多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。   例子1：四格卡方检验   以...
深度强化学习
m0_37852301的博客
09-07 459
基本概念 马尔可夫 在一个时序过程中，如果t+1时刻的状态仅取决于t时刻的状态St而与t时刻之前的任何状态都无关时，则认为t时刻的状态St具有马尔科夫性(Markovproperty)。若过程中的每一个状态都具有马尔科夫性，则这个过程具备马尔科夫性。具备了马尔科夫性的随机过程称为马尔科夫过程(Markovprocess)，又称马尔科夫链(Markovchain)。 状态转移概率矩阵 采样 从符合马尔科夫过程给定的状态转移概率矩阵生成一个状态序列的过程称为采样（sample）。 采样将得到一系列的状态转换
（二）马尔可夫决策过程
gls_nuaa的博客
03-29 4055
  从第一章中了解到强化学习中，智能体通过和环境进行交互获得信息。这个交互过程可以通过马尔可夫决策过程来表示，所以了解一下什么是MDP至关重要。   不过在了解马尔可夫决策过程之前，先要一些预备知识，它们分别叫马尔可夫性质、马尔可夫过程/马尔可夫链、马尔可夫奖励过程。   马尔可夫性质(Markov property)：如果一个状态的下一个状态只取决于当前状态，跟它当前状态之前的状态都没有关系。换句话说：未来的转移跟过去是独立的，只取决于现在。   给定一个状态的历史概念(其实就是过去状态的一个集合表示)：
机器学习——马尔可夫模型及马尔可夫决策过程（MDP）
热门推荐
zhongyoubing的博客
11-07 3万+
一、马尔可夫模型1. 马尔可夫链设表示随机变量X在离散时间t时刻的取值。若该变量随时间变化的转移概率仅依赖于它的当前值，即：也就是时候状态转移概率指依赖于前一个状态，称这个变量为马尔可夫变量，其中 为随机变量X可能的状态，这个性质称为马尔可夫性质，具有马尔可夫性质的随机过程称为马尔可夫过程。马尔可夫链是满足马尔可夫性质的随机过程，指在一段时间内随机变量X的取值序列（）满足上述性质2、转移概率马尔可夫
强化学习用于电力系统决策与控制（一）——频率调整
weixin_43753059的博客
11-03 3749
这里写自定义目录标题强化学习用于电力系统决策与控制（一）——频率调整1.频率调整（Frequency Regulation）FR2.三级频率调整结构3.如何将RL应用于FR（以AGC为例）1）环境、状态和动作：合理的创建标题，有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注脚注释也是必不可少的KaTeX数学公式新的甘特图功能，丰富你的文章UML 图表FLowchart流程图导
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值