题解-【模板】单源最短路径（弱化版）

【模板】单源最短路径（弱化版）

题目背景
本题测试数据为随机数据，在考试中可能会出现构造数据让SPFA不通过，如有需要请移步 P4779。

题目描述
如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式
输入格式：
第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：
一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例
输入样例#1：
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
输出样例#1：
0 2 4 3
说明
时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15；

对于40%的数据：N<=100，M<=10000；

对于70%的数据：N<=1000，M<=100000；

对于100%的数据：N<=10000，M<=500000。保证数据随机。

对于真正 100% 的数据，请移步 P4779。请注意，该题与本题数据范围略有不同。

样例说明：

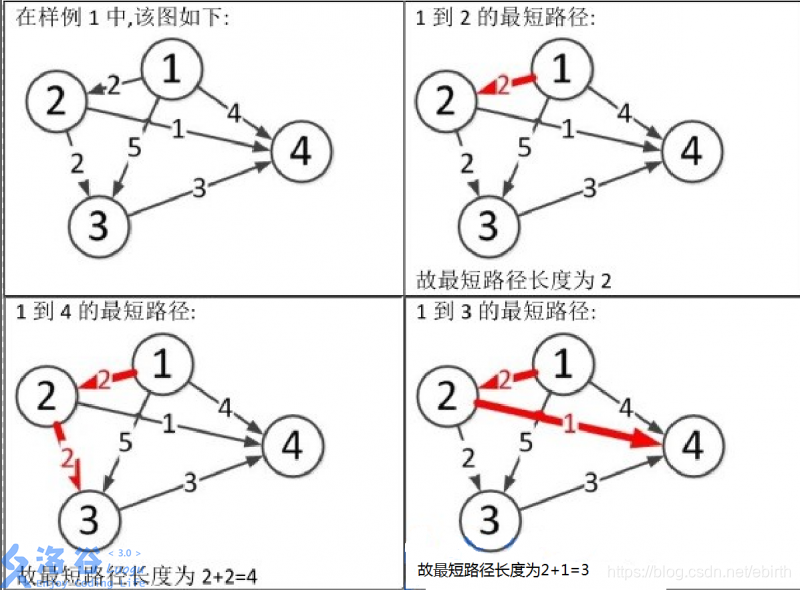
图片1到3和1到4的文字位置调换
思路：本题用SPFA算法可以完成，就是求有向图上一个原点到其他最短路的距离。
但是，这个题可能有负边权，就可以用SPFA算法来完成。原点到自身的距离为0，到其他原点