满二叉树、完美二叉树和完全二叉树概念解析 full tree&perfect tree&complete tree

因为各种教材关于树的很多定义都有较大差别，很多博客写的也很不统一，所以为了考试有个参考 有必要更新一下这篇！
本篇根据的教材是《算法导论》。

满二叉树(Full Binary Tree)

定义

所有的节点要么是叶节点（leaf node），要么是满节点（full node）。

回忆：
节点的深度 = 层数 - 1
树的高度height：任意节点的最大深度。
例如：只有一个节点的树的高度是0；空树的高度是-1。

完美二叉树 perfect binary tree

定义

直观理解：没有空位置，所有位置都被占满了。
严格定义：所有叶节点在同一层。

性质

假设一棵完美二叉树的总节点数为$n$，高度为$h$：

• 它的叶子数是：$2^h$，超过总节点数的一半
• 第k层的结点数是：$2^{k-1}$
• 总结点数是：$2^{h+1}-1$
• 高度$h=log(n+1)-1$
• 完美二叉树的总节点数一定是奇数。

完全二叉树 complete binary tree

定义

直观理解：只有最后一层，最后的位置能空出来。

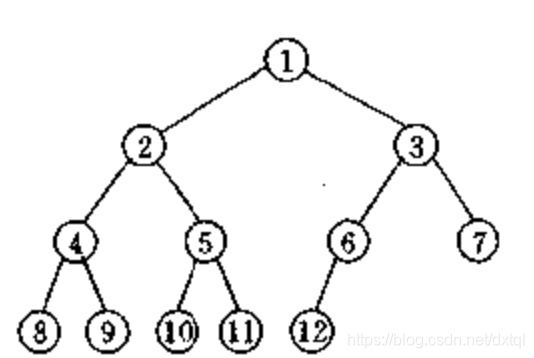
严格定义：
如果一棵树是高度为h的完全二叉树，当且仅当满足以下两种情况之一：

1. 左子树是高度为h-1的完美二叉树，右子树是高度为h-1的完全二叉树。
2. 左子树是高度为h-1的完全二叉树，右子树是高度为h-2的完美二叉树。

性质

总节点数：$n$，高度：$h$
高度 = $log(n)(向下取整)$