大厂面试高频算法题-全排列（回溯算法）

排列问题在高中数学中有学到的。n个不重复的数，全排列共有n！个。对于全排列问题，典型的解法就是回溯算法。

那么我们当时是怎么穷举全排列的呢？比方说给三个字符 [A,B,C]，你肯定不会无规律地乱穷举，一般是这样：先固定第一位为 A，然后第二位可以是 B，那么第三位只能是 C；然后可以把第二位变成 C，第三位就只能是 B 了；然后就只能变化第一位，变成 B，然后再穷举后两位……
其实这就是回溯算法，我们高中无师自通就会用，下面直接画出如下这棵回溯树：

解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考3个问题：
路径：也就是已经做出的选择。
选择列表：也就是你当前可以做的选择。
结束条件：也就是到达决策树底层，无法再做选择的条件。

下面还是通过一个决策树来说明：

为啥说这是决策树呢，因为你在每个节点上其实都在做决策。比如说你站在上图的绿色节点上，根据图上标出的 [路径] 跟 [选择列表]，可以把「路径」和「选择列表」作为决策树上每个节点的属性。我们定义的 backtrack 函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层，其「路径」就是一个全排列。

下面就是解决如何遍历这棵树，我想这个应该不难，本质上是对一个N叉树的for遍历加递归，这是回溯算法的一个基本的框架，其中的前序和后序遍历就是我们在根据问题具体写的处理逻辑了。

 /**
     * 二叉树遍历-递归
     * 前序（根左右）、中序（左根右）、后序（左右根）
     * @param root
     */
    public static void recursion(TreeNode<Object> root){
        if(null == root){
            return;
        }
        // 前序遍历1245673
        System.out.println(root.value);
        recursion(root.getLeft());
        // 中序遍历4265713
        // System.out.println(root.value);
        recursion(root.getRight());
        // 后序遍历4675231
        // System.out.println(root.value);
    }

这里递归的前序遍历一般是在进入某个节点之前做的操作，后序遍历一般就是在离开某个节点之后需要做的事情，这里使用逻辑来描述的话，就是“做出选择”和“撤销选择”，其中这个撤销选择向上回归就是一个典型的回溯算法。

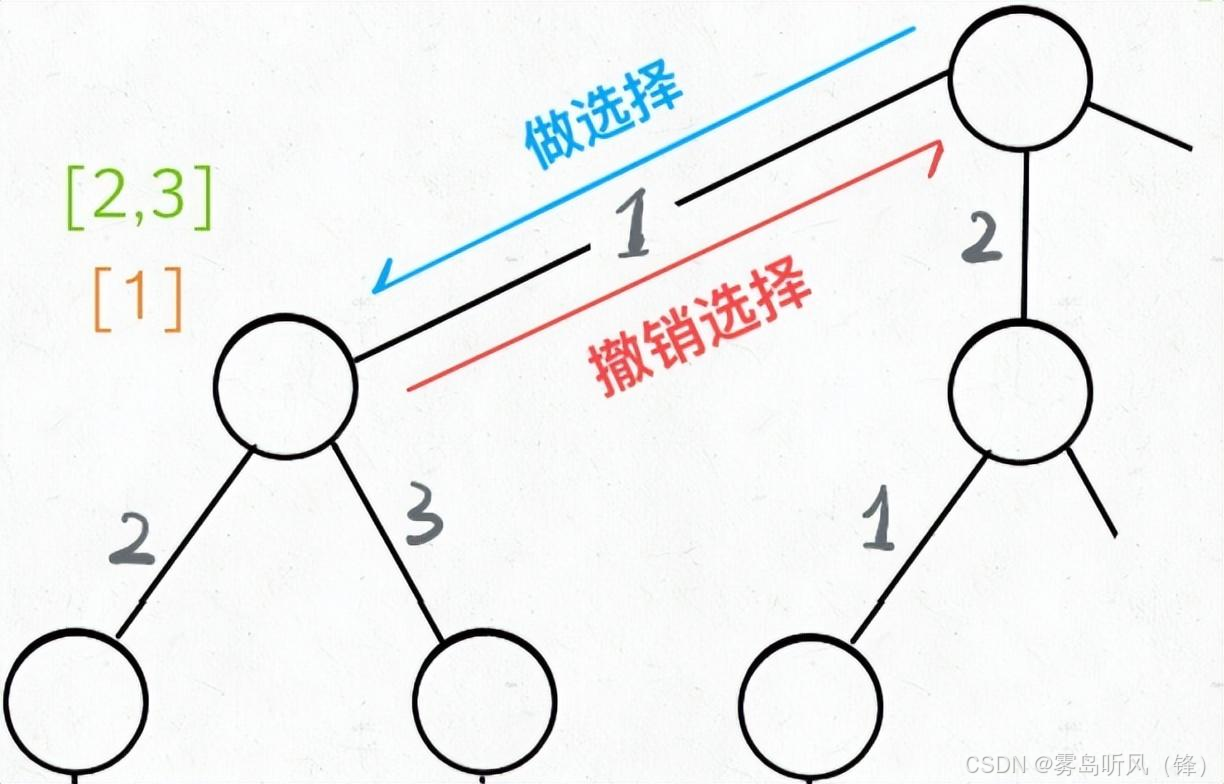通过以上的理解，我们只要在循环中，递归操作之前，做出选择，然后在递归之后，撤销之前的选择，这样我们就可以正确得到每个节点的选择列表和路径。

下面，直接上代码：

/**
     * 全排列
     * @param arr 不重复的字符数组
     * @return
     */
    public static List<List<String>> permute(String[] arr){
        if(arr.length == 0){
            return null;
        }
        // 记录结果
        List<List<String>> result = new ArrayList<>();
        // 记录路径
        List<String> track = new ArrayList<>();

        backtrack(arr,track,result);

        return result;
    }

    /**
     * 全排列-回溯算法
     * @param arr 选择列表，不存在track中的元素
     * @param track 路径
     * @param result 返回全部结果
     */
    public static void backtrack(String[] arr, List<String> track, List<List<String>> result){
        // 结束条件（arr中的元素全部在track中）
        if(arr.length == track.size()){
            result.add(new ArrayList<>(track));
            return;
        }
        for (int i = 0; i < arr.length; i++) {
            if(track.contains(arr[i])){ // 判断元素是否存在track中
                continue;
            }
            track.add(arr[i]); // 前序遍历，做选择
            backtrack(arr,track,result); // 进入下一次决策
            track.remove(track.size()-1); // 后序遍历，取消选择
        }
    }

最后总结

回溯算法就是个多叉树的遍历问题，关键就是在前序遍历和后序遍历的位置做一些操作，算法框架如下：

for 选择 in 选择列表:
    # 排除已选择的元素
    if (路径.contains(选择))
          continue;
    # 前序遍历，做选择
    路径.add(选择)
    backtrack(路径, 选择列表)
    # 后序遍历，撤销选择
    路径.remove(选择)

写 backtrack 函数时，需要维护走过的「路径」和当前可以做的「选择列表」，当触发「结束条件」时，将「路径」记入结果集。

思考，遗留问题：如果存在重复元素，如何去重？

创作不易，记得点赞+收藏 ^_^