归并排序求数组的逆序对数

将求数组的逆序对数问题穿插到归并排序，先求左部分逆序对，再求右部分的逆序对，最后在排序的过程中求跨中间的逆序对数，总的逆序对数是这三部分相加
先分：

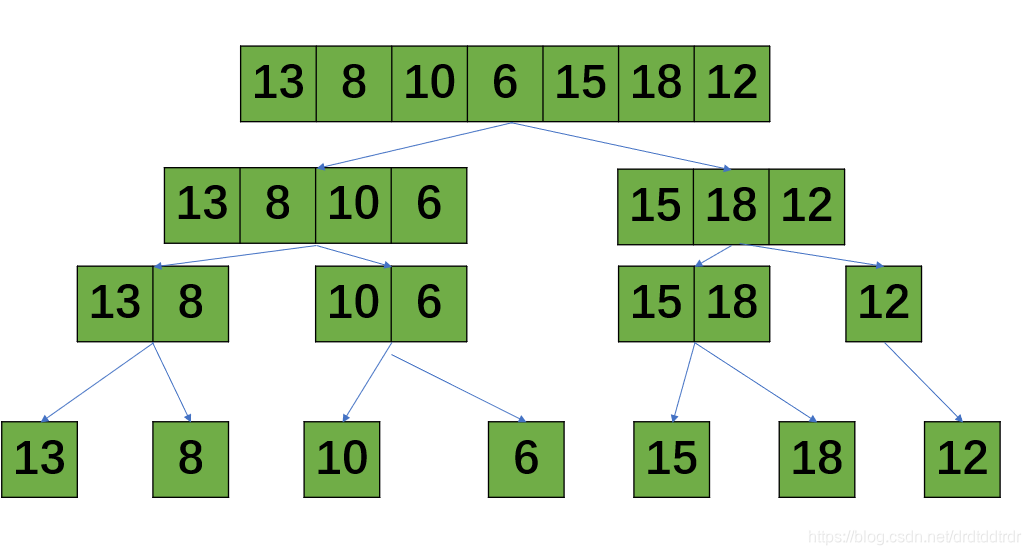
再治（S1：左部分的逆序对数；S2：右部分的逆序对数；S3：跨中间的逆序对数；下一个S1是这三个相加）

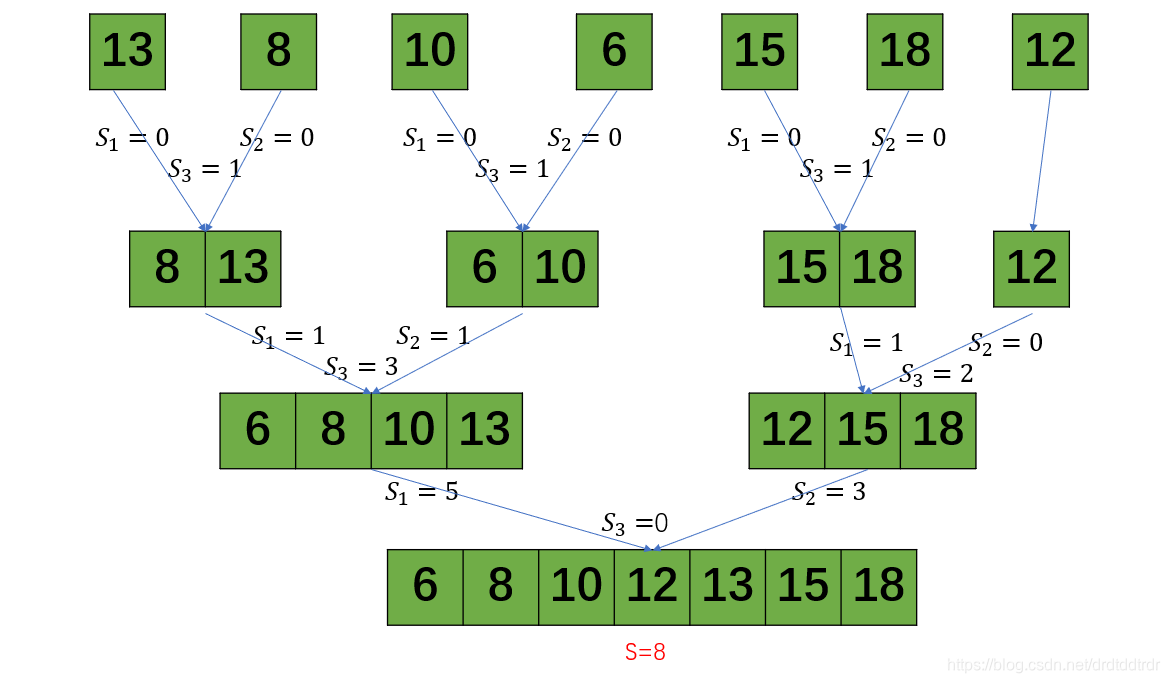
时间复杂度与归并排序一样都是nlogn；

#include<iostream>
using namespace std;

// 求跨中间逆序对数
int merge_count(int a[], int left, int mid, int right)
{
	int* b = new int[right - left + 1];          // 开辟和传进来的数组大小一致的空间，用来储存排序号的数组
	int P1 = left;                               // 原左数组的索引
	int P2 = mid+1;                              // 原右数组的索引   
	int i = 0;                                   // 新数组的索引
	int S3 = 0;
    
	// 循环遍历按顺序合并两个数组
	while (P1 <= mid && P2 <= right)
	{
		// 等于关系也不是逆序
		if (a[P1] <= a[P2])
		{
			b[i++] = a[P1++];
		}

	    // 如果是右边进去了，那么左边剩余的就是比这个进去的大的，也就是他们组成逆序对
		else
		{
			b[i++] = a[P2++];
			S3 += (mid - P1) + 1;      // 长度等于端点相减+1
		}
	}

	// 把剩余的拼接到新数组后面，这些剩余的不用再考虑逆序对了，因为前面已经考虑完了
	while (P1 <= mid)
	{
		b[i++] = a[P1++];
	}

	while (P2 <= right)
	{
		b[i++] = a[P2++];
	}


	// 把排好序的新数组给原数组，方便后面使用

	for (int i = 0; i < right - left + 1; ++i)
	{
		a[i + left] = b[i];         // 赋值从a[left]开始
	}

	delete[]b;      // 防止内存泄漏

	return S3;     // 返回结果

}

// 递归求解逆序对数
int count_inver(int a[], int left, int right)
{
	if (left >= right)
		return 0;                                  // 递归出口
	int mid = (left + right) / 2;
	int S1 =count_inver(a, left, mid);             // 求左半部分的逆序对数
	int S2 =count_inver(a, mid + 1, right);        // 求右半部分的逆序对数
	int S3 =merge_count(a, left, mid, right);      // 求跨中间的逆序对数
	return (S1 + S2 + S3);                         // 总逆序对数是三部分的逆序对数相加
}

int main()
{
	int a[7] = { 13,8,10,6,15,18,12};
	int ans = count_inver(a, 0, 6);
	cout << ans << endl;
	return 0;
}