次序选择问题

给定一个数组A，求出第k小的元素。
这是一个次序选择问题，求解方法多种，此处介绍在快排的思想上进行改造的分治算法。

原数组

原数组通过一次分解，求出随机选出的新主元的位置，该位置返回到主递归函数赋值给变量q

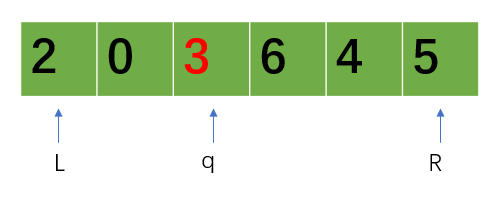
比较k和q的位置，若k在q的右边，则只对右边进行进一次拆分，若为左边则相反。直到q的位置刚好对应的是k所表达的位置，则此时q位置的元素为第k小的元素，因为它左边的都比它小，右边的都比它大。比较这一步要注意。

#include<iostream>
using namespace std;
#include<time.h>

// 随机选取主元并且把数组按照主元分解，并返回主元最后的位置（与快排完全一致）
int Randomized_Partition(int A[], int l, int r)
{

	
	int p = 0;                          // 交换媒介
	int P1 = l;
	int P2 = l;                         // 两个遍历下标 
	srand((time(NULL)));
	int s = rand() % (r - l) + 1 + l;   // 随机选取主元

	// 交换主元到末尾
	p = A[s];
	A[s] = A[r];
	A[r] = p;

	// 遍历分解原数组
	while (P2 < r)
	{
		// P2遍历到比主元小的，就把这个元素放到左边
		if (A[P2] <= A[r])
		{


			{
				p = A[P1];
				A[P1] = A[P2];
				A[P2++] = p;
				++P1;
			}

			}
		// 如果没有，就直接把P2往下；
		else
			++P2;
	}

	// 把主元放中间
	p = A[r];
	A[r] = A[P1];
	A[P1] = p;

	// 返回主元现在的位置
	return P1;
}

// 进行次序选择
int Randomized_Selection(int A[], int k,int l, int r)
{
	// 递归出口
	if (l >= r)
		return 0;

	// 分解原数组，并返回主元位置
	int p = Randomized_Partition(A, l, r);
	int x = 0;       // 保存结果

	// 判断是否找到的主元是我们要找的第k小的位置，注意这里的比较的表达式
	if (p-l+1 == k)
		return A[p];

	// 如果结果比k小，就找右边，注意这时候的k要减掉左边的元素
	if (p - l + 1 < k)
		x=Randomized_Selection(A, k - (p - l + 1), p +1, r);

	else
		x=Randomized_Selection(A, k, l, p-1);

	return x;

}

int main()
{
	int A[6] = { 3,2,5,6,0,4 };
	cout << "原数组为:";
	for (int i = 0; i < 6; ++i)
		cout << A[i] << " ";

	// 找第二小的元素
	int ans=Randomized_Selection(A,2, 0, 5);

	cout << "第二小的元素为:"<<ans<<endl;
	return 0;
}

时间复杂度：最快是n，最慢是n^2，期望是nlogn