31.岛屿的最大面积（medium）

最新推荐文章于 2025-12-05 17:02:52 发布

原创最新推荐文章于 2025-12-05 17:02:52 发布 · 889 阅读

30 ·

CC 4.0 BY-SA版权

文章标签：

#java #算法 #leetcode

1.题目链接：

695. 岛屿的最大面积 - 力扣（LeetCode）695. 岛屿的最大面积 - 给你一个大小为 m x n 的二进制矩阵 grid 。岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直的四个方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。岛屿的面积是岛上值为 1 的单元格的数目。计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。示例 1：[https://assets.leetcode.com/uploads/2021/05/01/maxarea1-grid.jpg]输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]输出：6解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。示例 2：输入：grid = [[0,0,0,0,0,0,0,0]]输出：0 提示： * m == grid.length * n == grid[i].length * 1 <= m, n <= 50 * grid[i][j] 为 0 或 1https://leetcode.cn/problems/max-area-of-island/description/2.题目描述：

给你一个大小为 m x n 的二进制矩阵 grid 。
    岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直的四个方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。
    岛屿的面积是岛上值为 1 的单元格的数目。
    计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

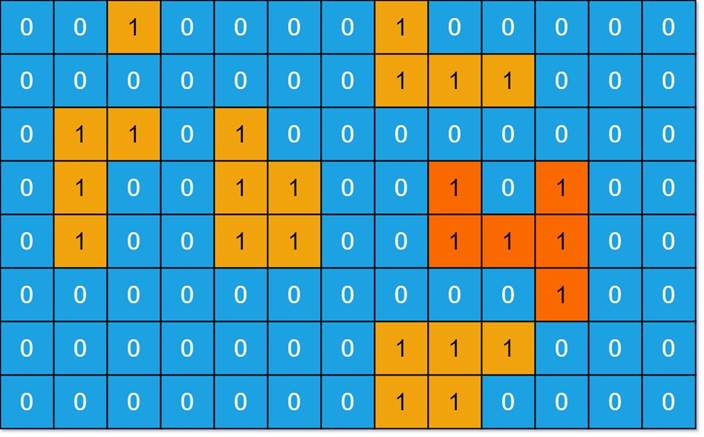
输入：

grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0], [0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：
答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：
输入：
grid = [[0,0,0,0,0,0,0,0]]
输出：0

提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 为 0 或 1

3. 算法思路：
•遍历整个矩阵，每当遇到一块土地的时候，就用「深搜」或者「宽搜」将与这块土地相连的「整个岛屿」的面积计算出来。

• •	然后在搜索得到的「所有的岛屿面积」求一个「最大值」即可。在搜索过程中，为了「防止搜到重复的土地」：
	◦	可以开一个同等规模的「布尔数组」，标记一下这个位置是否已经被访问过；
	◦	也可以将原始矩阵的 1 修改成 0 ，但是这样操作会修改原始矩阵。

4. 解法（深搜 dfs）：
算法流程：

•

主函数内：

a. 遍历整个数组，发现一块没有遍历到的土地之后，就用 dfs ，将与这块土地相连的岛屿的面积求出来；
b. 然后将面积更新到最终结果 ret 中。

•	深搜函数 dfs 中：

a. 能够进到 dfs 函数中，说明是一个没遍历到的位置；
b. 标记一下已经遍历过，设置一个变量 S = 1 （当前这个位置的面积为 1 ），记录最终的面积；
c. 上下左右遍历四个位置：

	如果找到一块没有遍历到的土地，就将与这块土地相连的岛屿面积累加到 S 上；
▪

d. 循环结束后，S 中存的就是整块岛屿的面积，返回即可。

Java算法代码：

class Solution {
    boolean[][] vis;
    int m,n;
    int[] dx = {0, 0, -1, 1};
    int[] dy = {1, -1, 0, 0};
    int count;
    public int maxAreaOfIsland(int[][] grid) {
        m = grid.length;n=grid[0].length;
        vis = new boolean[m][n];
        int ret = 0;
        for(int i = 0;i<m;i++)
            for(int j =0;j<n;j++)
            if(!vis[i][j] &&grid[i][j] ==1){
                count = 0;
                dfs(grid,i,j);
                ret = Math.max(ret,count);
            }
        return ret;
    }
    public void dfs(int [][] grid,int i,int j){
        count ++;
        vis[i][j] = true;
        for(int k =0;k<4;k++){
            int x = i+dx[k],y=j+dy[k];
            if(x>=0 && x<m&&y>=0&&y<n && !vis[x][y] &&grid[x][y] == 1)
            dfs(grid,x,y);
        }
    }
}

运行结果：