可调机械手动态解耦控制

可调串联机械手的动态解耦考虑变化的有效载荷

摘要

本文研究了具有变化负载的可调串联机械手的动态解耦问题。在无负载情况下，此类机械手可通过连杆反向旋转和质量的最优重新分配实现动态解耦。然而，引入变化的有效载荷会导致机械手动态解耦的扰动。为了消除此类扰动，本文讨论了最优控制设计。所提出的方法结合了机械与控制解决方案，改进了已有的设计概念，实现了考虑变化有效载荷的串联机械手动态解耦。通过使用MATLAB软件对所提技术的效率进行了评估。

关键词 机电设计 Serial机械手 Decoupled动力学 可调机构

1 引言

已知机器人机械手的动力学模型通常由一组非线性、强耦合的微分方程描述。复杂的动力学特性源于变化的惯性、不同关节之间的相互作用，以及科里奥利力和离心力等非线性力。非线性力会导致误差在高速下的位置响应，并且已被证明即使在低速时也具有显著影响。因此，机器人机构的动态解耦引起了研究人员的关注，并提出了不同的解决方案。

在最近的研究中 [5]，讨论了2自由度可调串联机械手的动态解耦问题。通过在具有可调长度连杆的初始结构上增加一个双Scott-Russell机构，并结合机械手连杆的相同且相反的旋转，实现了消除机械手动力学中非线性项的系数，即 [6] 与机械手连杆的相同且相反的旋转相结合，亦即 $h_1 = -h_2$（图 1）。

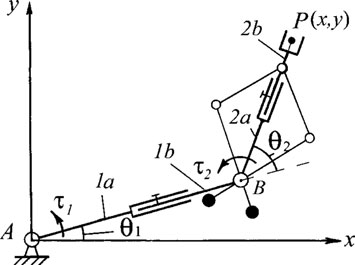
当可调串联机械手的第二连杆处于静态平衡时，即 $l_{BS2} = 0$（图1），且重力方向垂直于运动平面xOy时，运动方程可写为：

$$
\begin{bmatrix}
s_1 \
s_2
\end{bmatrix}
=
\begin{bmatrix}
I_{S2} + I_{S1} + m_1 l_{A S1}^2 + m_2 l_1^2 & I_{S2} \
I_{S2} & I_{S2}
\end{bmatrix}
\begin{bmatrix}
\ddot{h}_1 \
\ddot{h}_2
\end{bmatrix}
=
\begin{bmatrix}
a & b \
a & a
\end{bmatrix}
\begin{bmatrix}
\ddot{h}_1 \
\ddot{h}_2
\end{bmatrix}
\quad (1)
$$

其中，$a = I_{S2}$; $b = I_{S1} + m_1 l_{A S1}^2 + m_2 l_1^2$；$I_{S1}$ 是连杆1相对于其质心 $S_1$ 的轴向惯性矩；$I_{S2}$ 是连杆2相对于其质心 $S_2$ 的轴向惯性矩；$m_1$；$m_2$ 分别为连杆1 和连杆2的质量；$l_{A S1}$ 是连杆1的质心 $S_1$ 到关节中心A的距离；$l_{B S2}$ 是连杆2的质心 $S_2$ 到关节中心B的距离；$\dot{h}_1$ 是连杆1相对于基座的角加速度；$\dot{h}_2$ 是连杆2相对于连杆1的角加速度；

由这些方程可得

$$
\text{if: } \ddot{h}_1 = -\ddot{h}_2
\Rightarrow
\begin{cases}
s_1 = b \ddot{h}_1 \
s_2 = 0
\end{cases}
\quad (2)
$$

即动力学方程实现解耦，且第二个执行器扭矩被消除。

2 考虑负载的动态解耦

上述运动方程的动态解耦对应于无负载的机械手。然而，显然变化的有效载荷会在执行器上产生非线性的可变负载。

$$
\begin{cases}
s_1 = w(h_2) \ddot{h}_1 + [c_2 + b(h_2)] \ddot{h}_2 - 2a(h_2)\dot{h}_1\dot{h}_2 - a(h_2)\dot{h}_2^2 \
s_2 = [c_2 + b(h_2)] \ddot{h}_1 + c_2 \ddot{h}_2 + a(h_2)\dot{h}_1^2
\end{cases}
\quad (3)
$$

其中，

$$
a(h_2) = M_2 l_1 l_{B S2} \sin(h_2); \quad b(h_2) = M_2 l_1 l_{B S2} \cos(h_2); \quad w(h_2) = c_1 + c_2 + M_2 l_1^2 + 2b(h_2);
$$
$$
c_1 = I_{S1} + m_1 l_{A S1}^2; \quad c_2 = I_{S2} + M_2 l_{B S2}^2
$$

其中 $M_2 = m_2 + \Delta m$ 和 $l_{B S2} = \frac{\Delta m}{m_2 + \Delta m} l_2$, $\Delta m$ 是负载的质量。

因此，负载的引入导致机械手第二连杆的不平衡。根据上述提出的解决方案，动力学方程可重写为：

$$
\begin{cases}
s_1 = (I_{S1} + m_1 l_{A S1}^2 + m_2 l_1^2) \ddot{h}_1 + \Delta m l_1 [l_1 + l_2 \cos(h_2)] \ddot{h}_1 - \Delta m l_1 l_2 \sin(h_2) \dot{h}_1 \dot{h}_2 \
s_2 = \Delta m l_1 l_2 \cos(h_2) \ddot{h}_1 + \sin(h_2) \dot{h}_1^2
\end{cases}
\quad (4)
$$

显然，执行器的扭矩大大简化了，但它们仍未完全解耦。与公式(2)相比，负载补偿可通过以下方式获得：

$$
\begin{cases}
\Delta s_1 = \Delta m l_1 [l_1 + l_2 \cos(h_2)] \ddot{h}_1 - \Delta m l_1 l_2 \sin(h_2) \dot{h}_1 \dot{h}_2 \
\Delta s_2 = \Delta m l_1 l_2 \cos(h_2) \ddot{h}_1 + \sin(h_2) \dot{h}_1^2
\end{cases}
\quad (5)
$$

3 实例研究的计算机仿真

为了评估所提出技术的性能，进行了带有负载补偿和不带负载补偿的仿真。首先，为了说明负载补偿的影响，使用了开环控制系统，即一种无反馈系统。

3.1 开环控制系统

开环控制律可以表示为：

$$
\begin{cases}
s_1(t) = (a + b) \ddot{h} {1R}(t) + a \ddot{h} {2R}(t) + \Delta s_{1R} \
s_2(t) = a \ddot{h} {1R}(t) + a \ddot{h} {2R}(t) + \Delta s_{2R}
\end{cases}
\quad (6)
$$

其中，负载补偿由以下给出：

$$
\begin{cases}
\Delta s_{1R} = \Delta m l_1 [l_1 + l_2 \cos(h_{2R})] \ddot{h} {1R} - \Delta m l_1 l_2 \sin(h {2R}) \dot{h} {1R} \dot{h} {2R} \
\Delta s_{2R} = \Delta m l_1 l_2 \cos(h_{2R}) \ddot{h} {1R} + \sin(h {2R}) \dot{h}_{1R}^2
\end{cases}
\quad (7)
$$

其中，

$$
\begin{cases}
h_{1R}(t) = h^i_1 + (h^f_1 - h^i_1) \left( \frac{t}{T} \right)^3 \left(10 - 15 \frac{t}{T} + 6 \left( \frac{t}{T} \right)^2 \right) \
h_{2R}(t) = h^i_2 + (h^f_2 - h^i_2) \left( \frac{t}{T} \right)^3 \left(10 - 15 \frac{t}{T} + 6 \left( \frac{t}{T} \right)^2 \right)
\end{cases}
\quad (8)
$$

其中，$T$ 是执行轨迹所用的时间， $0 \leq t \leq T$。而 $\dot{h} {1R}, \dot{h} {2R}, \ddot{h} {1R}, \ddot{h} {2R}$ 可通过连续求导获得。

机械手的初始和最终位置为：$h^i_1 = 0.576; h^i_2 = 0$ 和 $h^f_1 = 1.92; h^f_2 = -1.344$。轨迹 $h_{1R}(t)$ 和 $h_{2R}(t)$ 是时间函数，满足 $[h_{1R}(0), h_{2R}(0)]^T = [h^i_1, h^i_2]^T$ 和 $[h_{1R}(T), h_{2R}(T)]^T = [h^f_1, h^f_2]^T$。由于轨迹由时间参数化，我们可以通过微分得到轨迹上的速度和加速度。

如 $h^f_2 = h^i_1 + h^i_2 - h^f_1 \Rightarrow \ddot{h} {2R}(t) = -\ddot{h} {1R}(t)$ 且 $\dot{h} {2R}(t) = -\dot{h} {1R}(t)$。

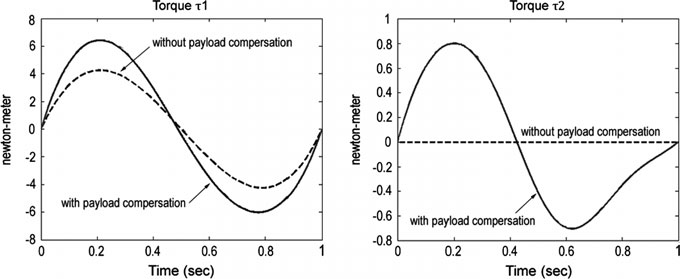
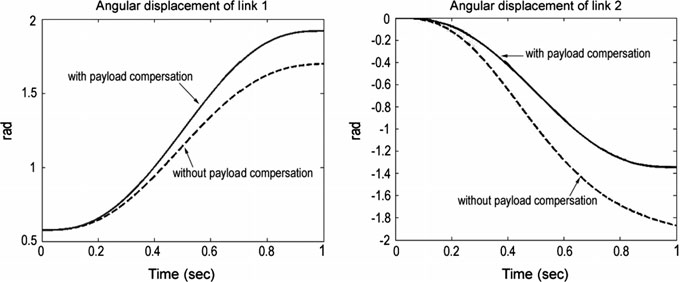
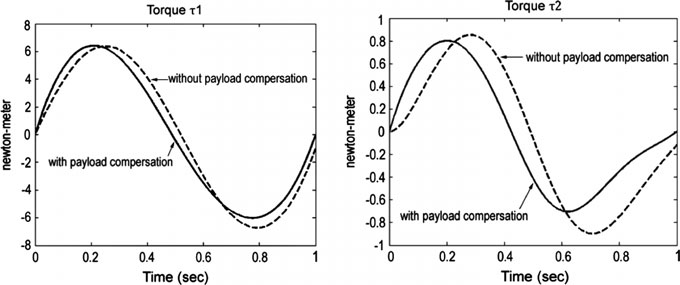
对于 $T = 1\,\text{s}$ 和 $\Delta m = 1\,\text{kg}$，第 3 节中所示机械手在 MATLAB 软件中的响应如图 2 和 3 所示。

虚线表示未进行负载补偿时机械手的扭矩和角位移，实线表示进行负载补偿后的相应参数。因此可以看出这两种情况之间存在误差。在有负载补偿的情况下，机械手的两个连杆均能准确旋转至目标角度。然而，在没有负载补偿的情况下，连杆1和连杆2的角位移误差分别为39%和16.5%。这验证了考虑负载的前馈控制的效果。因此，在无负载补偿的情况下，需要采用反馈控制来减小误差。

3.2 闭环控制系统

闭环控制律可以表示为：

$$
\begin{cases}
s_1(t) = (a + b) \ddot{h} {1R}(t) + a \ddot{h} {2R}(t) + \Delta s_{1R} \
\quad - g_{11} \left[ (a + b)(\dot{h} 1(t) - \dot{h} {1R}(t)) + a(\dot{h} 2(t) - \dot{h} {2R}(t)) \right] \
\quad - g_{12} \left[ (a + b)(h_1(t) - h_{1R}(t)) + a(h_2(t) - h_{2R}(t)) \right] \
\
s_2(t) = a \ddot{h} {1R}(t) + a \ddot{h} {2R}(t) + \Delta s_{2R} \
\quad - g_{21} \left[ a(\dot{h} 1(t) - \dot{h} {1R}(t)) + a(\dot{h} 2(t) - \dot{h} {2R}(t)) \right] \
\quad - g_{22} \left[ a(h_1(t) - h_{1R}(t)) + a(h_2(t) - h_{2R}(t)) \right]
\end{cases}
\quad (9)
$$

其中，$\Delta s_{1R}(t)$ 和 $\Delta s_{2R}(t)$ 由公式(7)给出。

常数增益元素 $g_{11}$、$g_{12}$、$g_{21}$ 和 $g_{22}$ 通过状态反馈的最优极点配置设计获得。该静态平衡的 2自由度可调串联机械手 的状态空间表示将写作：

$$
\begin{bmatrix}
\ddot{h}_1 \
\dot{h}_1 \
\ddot{h}_2 \
\dot{h}_2
\end{bmatrix}
=
\begin{bmatrix}
0 & 1 & 0 & 0 \
0 & 0 & 0 & 0 \
0 & 0 & 0 & 1 \
0 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
\dot{h}_1 \
h_1 \
\dot{h}_2 \
h_2
\end{bmatrix}
+
\begin{bmatrix}
0 & 0 \
1 & 0 \
0 & 0 \
-\frac{1}{b} & \frac{1}{a} + \frac{1}{b}
\end{bmatrix}
\begin{bmatrix}
s_1 \
s_2
\end{bmatrix}
\quad (10)
$$

可控标准型由以下两个独立的子系统给出：

$$
\begin{cases}
(a + b) \ddot{h}_1 + a \ddot{h}_2 \
(a + b) \dot{h}_1 + a \dot{h}_2
\end{bmatrix}
=
\begin{bmatrix}
0 & 0 \
1 & 0
\end{bmatrix}
\begin{bmatrix}
(a + b) \dot{h}_1 + a \dot{h}_2 \
(a + b) h_1 + a h_2
\end{bmatrix}
+
\begin{bmatrix}
1 \
0
\end{bmatrix}
s_1 \
\
\begin{bmatrix}
a \ddot{h}_1 + a \ddot{h}_2 \
a \dot{h}_1 + a \dot{h}_2
\end{bmatrix}
=
\begin{bmatrix}
0 & 0 \
1 & 0
\end{bmatrix}
\begin{bmatrix}
a \dot{h}_1 + a \dot{h}_2 \
a h_1 + a h_2
\end{bmatrix}
+
\begin{bmatrix}
1 \
0
\end{bmatrix}
s_2
\end{cases}
\quad (11)
$$

一个双积分器 $\ddot{u}(t), \dot{u}(t)$ 构成的系统是完全可控的。我们寻求使代价函数 $J = \int_0^{T_p} x^T Q x + u^T R u \, dt$ 最小化的控制律，其中矩阵 $Q$ 基于如下定义的可控性格拉米矩阵：

$$
G_c(0, T_p) = \int_0^{T_p} e^{At} B B^T e^{A^T t} dt
$$

矩阵 $Q = \left(G_c(0, T_p)\right)^{-1}$ 是对称正定的。参数 $T_p$ 假设闭环系统的极点可在S平面中位于横坐标为 $-1/T_p$ 的垂直直线左侧。

线性二次型控制器是唯一的最优解 $u(t) = -G x(t)$，即具有 $G = B^T R$ 的全状态反馈控制律，可使代价函数 $J$ 最小化。矩阵 $R$ 是代数Riccati方程：$A^T R + R A - R B B^T R + Q = 0$ 的唯一对称正定解。因此，

$$
g_{11} = g_{12} = \frac{2 \sqrt{1 + \sqrt{3}}}{T_p}; \quad g_{21} = g_{22} = \frac{2}{T_p^2 \sqrt{3}}
$$

然后，闭环特征多项式为：
$$
P(s) = s^2 + 2 \frac{\sqrt{1 + \sqrt{3}}}{T_p} s + \frac{2}{T_p^2 \sqrt{3}}
$$

如果 $P(s) = s^2 + 2\zeta \omega_n s + \omega_n^2$，我们有：$\omega_n = \sqrt{\frac{2}{T_p \sqrt{3}}}$ 和 $\zeta = \frac{\sqrt{1 + \sqrt{3}}}{\sqrt{2 \sqrt{3}}} = 0.89$

对于 $T = 1\,\text{s}$；$T_p = 0.2\,\text{s}$ 且 $\Delta m = 1\,\text{kg}$ 时，MATLAB软件得到的响应如图 4 和 5 所示。与之前的情况一样，虚线表示未进行负载补偿的机械手扭矩和角位移，实线表示进行了补偿后的相同参数。与之前的仿真一样，负载补偿能够实现机械手运动的精确复现。

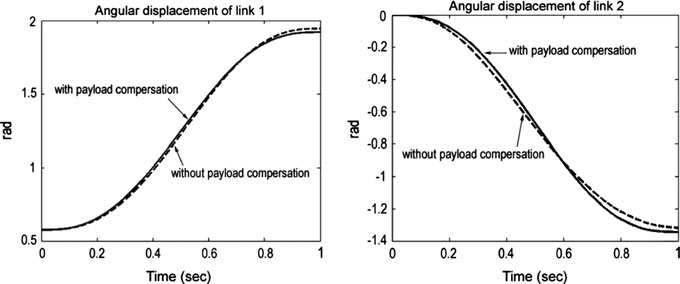
与这些结果相比，未进行负载补偿时连杆1和2的角位移误差（图4和 5）不超过2%。因此，使用反馈可以进一步减少因消除负载补偿而引起的误差。

4 结论

具有连杆可调长度的串联机械手在先前的研究中可以通过连杆反向旋转和质量的最优重新分配实现动态解耦。然而，显然引入变化的有效载荷会导致机械手动态解耦的扰动。为了确保在负载变化时机械手仍具有线性化解耦动力学，采用了一种最优控制技术。

因此，实现了考虑变化的有效载荷的机械手的完全动态解耦。为了评估所提出技术的效率，在开环控制系统（即无反馈系统）和闭环控制系统中分别进行了带有负载补偿和不带负载补偿的仿真。通过使用MATLAB软件获得的结果表明了所提出解决方案的有效性。

最后需要指出的是，与其它方案相比，所提出的设计概念能够在运动连杆的总质量相对较小增加的情况下实现具有解耦动力学的机械手，并且考虑了变化的有效载荷。该方案可在固定序列机械手的设计中得到广泛应用，以实现对夹持器运动的精确复现。