介电泳-场流分离微流控装置建模

医疗器械传感器 2018;1:e10007. wile y onlinelibrar y .com/期刊/mds3

6的| 1
htt p s://doi.or g /10.1002/mds3.10007
©2018威利期刊公司

1|引言

目前，人们对开发基于血液的非传染性疾病（NCDs）筛查方法/技术 表现出极大的兴趣，尤其是癌症的筛查（阿利克斯‐帕纳比耶雷斯和潘 特尔，2016；海策尔、佩拉基斯、盖格尔和施派歇尔，2017）。基于 血液的非传染性疾病筛查是一种快速且具有成本效益的方法，可实现 疾病的早期检测，并对患者造成最小的压力；这些特点使得基于血液 的筛查方法能够提高筛查频率。非传染性疾病的血液筛查发展依赖于 识别和分离患者血液样品中的生物标志物，包括稀有血细胞（阿利克 斯‐帕纳比耶雷斯和潘特尔，2016；海策尔等，2017）。与癌症相关 的稀有血细胞是循环肿瘤细胞（阿利克斯‐帕纳比耶雷斯和潘特尔，2016；Heitzer等， 2017）。已开发出多种基于微流控器件的方法/技术，用于识别和分 离循环中的稀有血细胞（安特福克和劳雷尔，2017；萨吉什和森， 2014）。微流控器件具有多个特性，使其非常适合从血液样品中识别 和分离循环稀有血细胞。其优势包括更高的表面积密度、增强的传递 系数以及更低的样品和试剂需求。一种用于稀有血细胞基于血液的筛 查方法/技术是场流分离（FFF）（安特福克和劳雷尔，2017；休斯， 2002）。FFF代表一类分离技术，利用垂直于流动方向的外场，将含 有不同微物体的样品分离成多个各自含有相似微物体的样品。

微物体（申德鲁克和斯莱特，2012）。已采用多种外场（包括介电泳 （DEP））来实现场流分离。外场的选择决定了微物体分离所依据的 物理特性。

介电泳是指浸没在导电介质中的中性但可极化的微物体，相对于 电场梯度空间分布所产生的受力现象（朱贝里、斯里瓦斯塔瓦和达塔， 2014；Khoshmanesh等,2011；摩根和格林，2015）。当微物体被 吸引至电场梯度最高区域时称为正向介电泳（pDEP），而被排斥至 电场梯度最低区域时称为负向介电泳（nDEP）（Jubery等,2014； Khoshmanesh等,2011；摩根和格林，2015）。在介电泳‐场流分 离微流控装置中，负向介电泳力与沉降力共同作用，使每个微物体在 微通道内移动到一个独特的垂直位置，该位置取决于微物体及其周围 介质的性质（密度、电导率和介电常数）；这导致所有具有相同介电 常数和密度的微物体形成一个单一的样品层。介电泳‐场流分离微装置 根据微物体的类型而非尺寸进行分离（Jubery等,2014；摩根和格林， 2015）。图1为典型的连续流动介电泳‐场流分离微流控装置中微物体 分离的示意图。利用介电泳进行细胞分离的优势在于，它不需要像荧 光激活细胞分选仪或磁激活细胞分选仪那样进行免疫标记，从而避免 了在芯片上集成光学元件或电磁铁及永磁体的需求（Kayani, Khoshmanesh,Ward,Mitchell,&Kalantar‐zadeh,2012；李、 黄和金，2016）。

微物体在介电泳力‐场流分离微装置中的路径取决于电场，而电场 又依赖于电极的排列方式。因此，需要针对每种电极排列单独分析微 物体路径的依赖性，正如本文所进行的研究。图2示出了本文分析的 电极排列示意图；该排列由有限长度（we）的电极组成，电极沿微通 道的整个宽度（Wch）延伸，并布置在微通道的上下壁面上。微通道 上壁面的电极和电极间隙分别与下壁面的电极间隙和电极对齐。

对颗粒流的动态建模通常采用欧拉或拉格朗日方法（埃尔戈巴希， 2003；范瓦赫姆和阿尔姆斯泰德，2003）。欧拉方法假设流体和颗 粒为相互穿透的连续介质彼此相互作用。因此，两相的控制方程类似于流体的控制方程（埃尔 戈巴希，2003；范瓦赫姆和阿尔姆斯泰德，2003）。另一方面，拉 格朗日建模将流体视为连续介质，而将颗粒视为离散实体。对于拉格 朗日方法，流体的控制方程为连续性方程和纳维‐斯托克斯方程，而每 个颗粒的行为则由牛顿第二定律描述（埃尔戈巴希，2003；范瓦赫姆 和阿尔姆斯泰德，2003）。这两种方法各有优缺点，文献中已有详细 说明（范瓦赫姆和阿尔姆斯泰德，2003）。研究人员主要采用拉格 日方法对基于介电泳的微器件中微物体的路径进行动态建模。黄、王、 贝克和加斯科因（1997）建立了一个经过实验验证的基于介电泳的微 器件静态模型，该器件采用叉指换能器（IDT）电极，用于场流分离。

李和巴希尔（2004）建立了使用IDT电极的基于介电泳的微流控装置 模型，用于捕获细胞和微粒等微物体；他们利用该模型进行了参数研 究。克拉尔、利斯、施密特和延森（2006）提出并实验验证了一种微 流控装置的准动态模型，该装置采用倾斜IDT电极实现介电泳，用于 场流分离。朱贝里和杜塔（2013）对具有独特电极构型的微流控器件 进行了基于模型的研究，以同时在垂直和水平方向上实现介电泳力。

马修、阿拉扎姆、哈桑和埃尔‐哈萨尼（2016）开发了介电泳‐场流分 离微流控装置的动态模型，其电极构型包括位于微通道顶面的无限长 电极和底面上的有限尺寸电极。青木、白井、内田和远久保（2016） 数值研究了一种带有平面IDT电极的基于介电泳的微流控装置，用于 捕获颗粒。阿里和朴（2016）对采用“液体电极”的基于介电泳的微 流控装置进行了动态建模，用于分离正常血液中的组分（红细胞、白 细胞和血小板）。

本文首次分析了微通道中微物体在图2所示电极排列下的运动路 径；文献中的几乎全部分析都涉及IDT电极。本文提出的动态模型不 同于文献中的静态模型，能够预测轴向位移以及达到稳态垂直位置所 需的时间。过去已实现微通道上下表面带有电极的微流控器件，且具 有类似特性。微加工工艺布局可用于制造本文分析的微流控装置（Li,Li,Zhang, Alici,&Wen,2014）。

2|理论

本文分析的电极排列如图2所示。方程1表示介电泳‐场流分离微流控装 置中任意微物体运动路径的控制方程（Maxey&Riley,1983）。方 程1考虑了惯性、沉降（重力与浮力相关力之差）、阻力、虚拟质量 和介电泳力的作用（Maxey&Riley,1983）。需要强调的是，大多 数基于介电泳的微流控装置处理的是稀悬浮液，因此只需分析单个微 物体的路径，而非总体浓度；该模型所基于的所有假设在文献中已有 详细说明（Mathew等人，2016）。Re[fCM]在方程2中给出，对应 于在处理微粒的微流控器件中实现负向介电泳（nDEP）的情况；操 作频率（>1 MHz）需要非常高，从而可以忽略电导率对Re[fCM]的影响 （Jubery等,2014；Khoshmanesh等,2011）。由于微流控器件中 常见的低流速，流动为充分发展流。充分发展流的速度由方程3给出 （Mathew等人，2016）。初始位移和速度由方程4给出。

(1) Ẍo+ 9μm (2ρo+ρm)R2o Ẋo− ρm (2ρo+ρm) U̇m− 9μm (2ρo+ρm)R2o Um + 2(ρo−ρm) (2ρo+ρm) G− 1.5εmRe[fCM] (2ρo+ρm) |E|2= 0

(2) Re[fCM]= Re[o−m o+2m]

(3) Um=[6 Qm αH2 ch( y Hch − y2 H2 ch) , 0] T

(4) Xo(t= 0)=[0, Hch 2] T and Ẋo(t= 0)=[32 Qm αH2 ch ,0] T

方程1所需的电场信息是基于电势计算的，电势通过拉普拉斯方 程描述，并按照文献中所述方法进行数值求解（Mathew等人， 2016）。时间步长取为10−4秒，且用于α= 20方程1。本文建立的模 型对于设计本文所述的介电泳‐场流分离微流控装置特别有用，因为 它考虑了所有相关的几何和操作参数。方程1可推广至其他电极构型， 其中电场为二维，如图2所示电极构型所对应的电场。

Khoshmanesh等人（2011）详细介绍了可用于基于介电泳分离的多 种电极构型。在将方程1扩展到图2分析之外的电极构型时，必须注意 确保E2对应于所考虑的电极构型。

3 | 结果与讨论

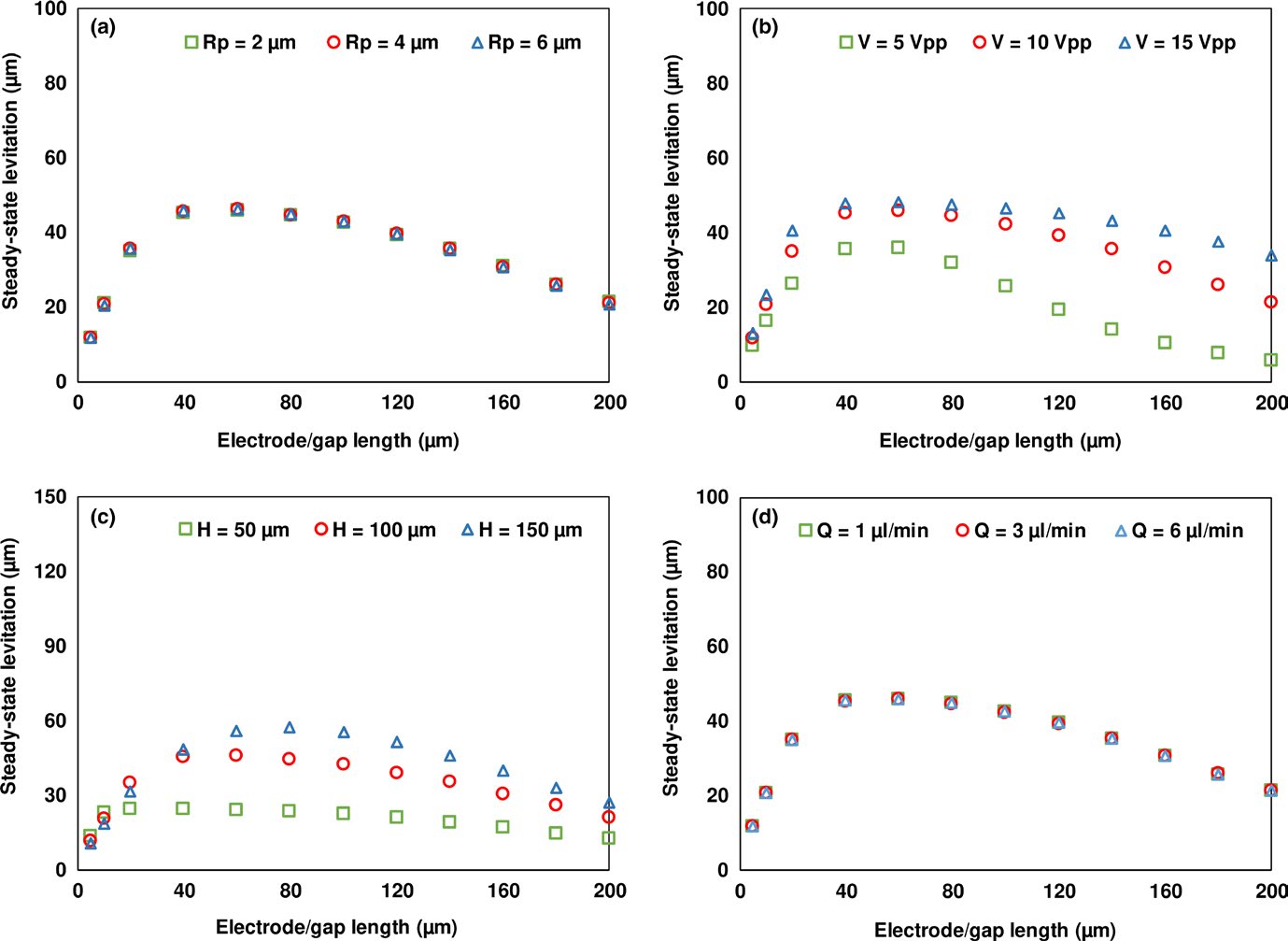
通过参数研究获得的结果在本文的下一部分中进行分析，以理解微物体稳态垂直位置与各参数之间的关系。研究采用水（μ m = 10−3 Pas，ρ m = 998 kg/m3,和 ε m =78.5）作为介质，聚苯乙烯（ρ p =1,055 kg/m3和ε p =2.55）微物体（Mathew等人，2016）。图3表示稳态垂直位置对电极和间隙尺寸的依赖关系，不受其他参数影响。随着电极和间隙尺寸的增加，稳态垂直位置起初上升至最大值，随后下降。这表明存在一个电极和间隙尺寸的阈值，超过该阈值后稳态垂直位置不再增加。在低于该阈值的电极和间隙长度范围内，电极和间隙尺寸的增加会导致垂直位置的升高；电极和间隙尺寸的增加当电极和间隙尺寸超过阈值时，垂直位置会降低。当上下电极的电极和间隙尺寸均减小至低于阈值尺寸时，每组电极的作用类似于非常长的单个电极，导致电场非均匀性下降，从而降低介电泳力和垂直位置。当电极和间隙尺寸增大并超过阈值电极和间隙尺寸时，相应电场的强度会低于阈值电极和间隙尺寸下的电场强度，从而导致介电泳力以及垂直位置的下降。

图3描绘了稳态垂直位置对各个参数的依赖关系。图3a表示在广泛的电极和间隙尺寸范围内，稳态垂直位置对半径的依赖性；可以看出，半径对稳态垂直位置的影响很小。由于沉降力和介电泳力均与微物体的半径相关，因此在沉降力与介电泳力平衡的稳态垂直位置处，半径的影响不显著。从图3b可以看出，对于所有电极和间隙尺寸，施加电压的增加会导致微物体稳态垂直位置的升高。施加电压的增加使得在整个微通道高度范围内介电泳力增强，从而增加了沉降力与介电泳力平衡点距离下壁面的距离。图3c分析了在广泛范围的电极和间隙尺寸下，微物体稳态垂直位置对微通道高度的依赖性。可以观察到，微通道高度的增加导致稳态垂直位置上升。这是因为当微通道高度减小时，介电泳力沿高度方向的衰减速率变得更陡峭，使得与介电泳力相平衡的沉降力更靠近下壁面。图3d展示了微物体稳态垂直位置对体积流量的依赖性，结果表明该影响可忽略不计。这种行为是预期之中的，因为流速仅影响水平位移，而不影响垂直位移，如方程1所示。

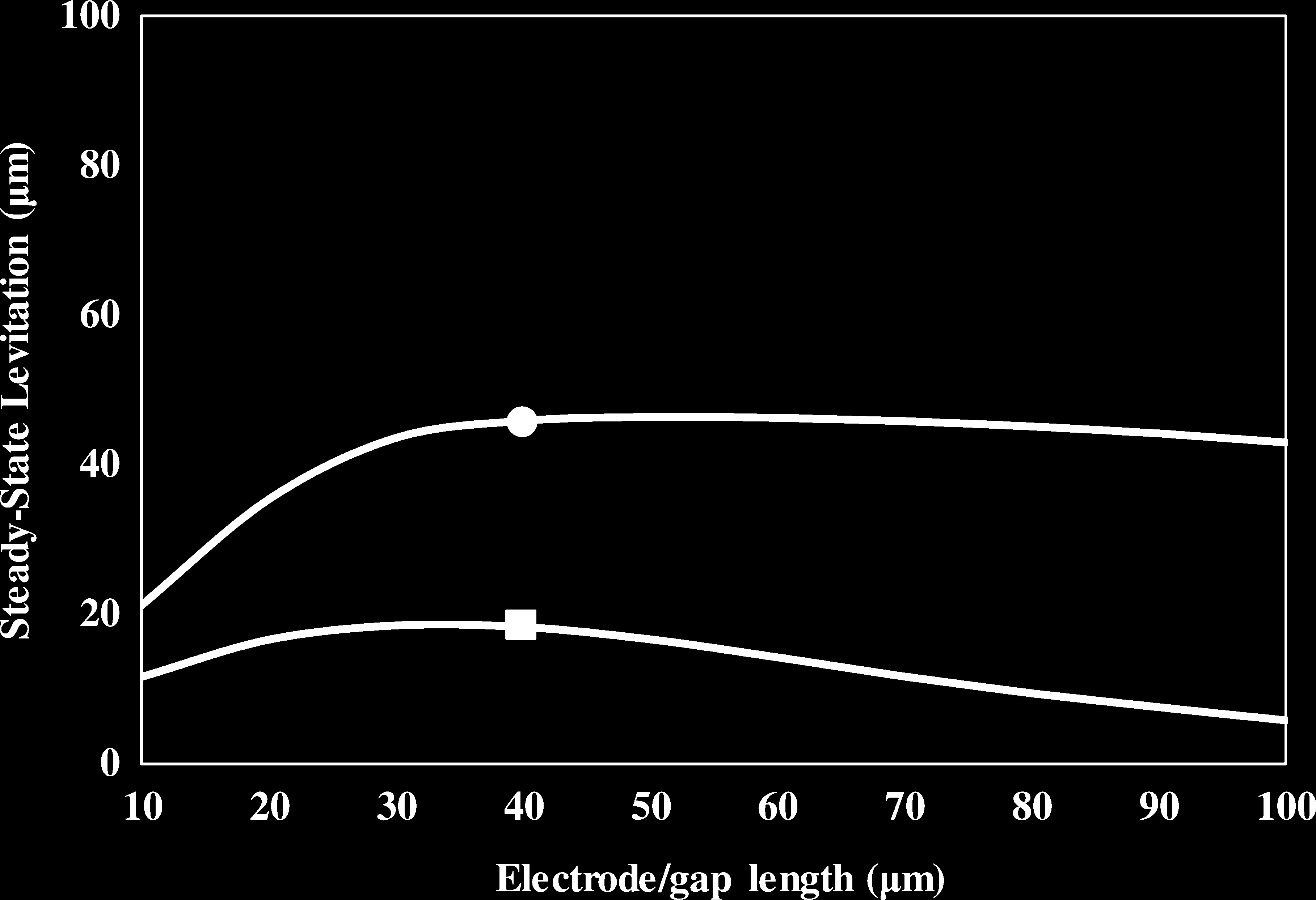
如前所述，介电泳‐场流分离微流控装置可以通过将每种微物体悬浮至特定高度来实现基于类型的选择性分离。图4展示了该介电泳‐场流分离微流控装置在按类型分离微物体方面的效能。图4显示了两种不同微物体——二氧化硅（ρ p = 2,000kg/m3 和ε p =3.5）和聚苯乙烯微粒——在其他所有参数保持不变的情况下的运动轨迹（ Khoshmanesh等，2010）。从图中可以看出，当受到介电泳力作用时，二氧化硅和聚苯乙烯微粒具有不同的悬浮高度，这使得此类微物体的异质混合物能够被分离为均质的二氧化硅样品和聚苯乙烯微粒样品。

4|结论

基于介电泳力的微装置动态模型的开发及其在场流分离中的参数研究应用本文记录了相关研究结果。参数研究使用水和聚苯乙烯微粒进行。在微通道的上下壁面放置了具有有限长度且贯穿微通道全宽度的电极；每个上部电极和电极间隙分别与下部的电极间隙和电极对齐。该模型考虑了惯性、阻力、沉降、虚拟质量和介电泳力等相关作用力。根据该模型，稳态垂直位置依赖于施加电压和微通道高度，而不依赖于微物体半径和流速。此外，模型还揭示了在其他所有参数固定的情况下，存在一个最佳电极和间隙长度，使得稳态垂直位置达到最大值。

符号说明

E=[E x,Ey] T 电场矢量，V/m
fCM 克劳修斯‐莫索蒂因子
G=[0,g]T 重力加速度矢量，米/秒2
ge 电极间隙长度，米
Hch 微通道高度，米
Qm 介质的体积流量，米3/秒
Um 介质速度矢量，米/秒
V 施加电压，Vpp
Wch 微通道宽度，米
we 电极长度，米
X o =[xo,y o] T 微物体位移矢量，米
xo 微物体在水平方向的位移方向，m
yo 微物体垂直方向位移方向 , m
α= W ch / H ch ≫1 微通道的宽高比
ρm 介质密度，kg/m3
ρ o 微物体密度，kg/m3
ε m 介质介电常数，法/米
ε o 微物体的介电常数，F/m