超低功耗双尾锁存比较器设计

用于生物医学应用的超低功耗双尾锁存比较器的设计与分析

1 引言

比较器是模数转换器的主要构成模块之一，广泛应用于多种信号处理应用中。一个新兴的应用领域是植入式医疗设备（IMD）。这类设备通常由电池供电，且能量受限严重。由于更换植入设备通常需要手术，存在风险且成本高昂，因此非常不便。为了延长电池寿命，设计超低功耗电路具有重要意义。

我们旨在为特定系统设计一款低功耗比较器，该系统为低功耗压缩采样电路。该系统涉及稀疏信号的采集，例如在小波域中具有稀疏性的心电图（ECG）信号。该系统面向低功耗无线植入式医疗设备，如心脏植入式医疗设备。由于生命体征信号变化较慢，系统对速度要求不高，而功耗是主要考虑因素。本系统采用工作在100千赫兹时钟频率下的7位逐次逼近型模数转换器，足以满足预期用途；但整个植入式医疗设备的功耗必须低于10微瓦，以支持约10年的使用时间。

本文针对功耗和开关时间，对传统双尾锁存器比较器的架构进行了优化。特别是，对该比较器进行了优化，使其能够在低电源电压下工作。电压范围为400毫伏至1伏特，时钟频率范围为50至200千赫兹。然而，所提出的比较器拓扑结构并不完全局限于该应用。根据本研究中所述工作区域附近的条件，可对比较器进行重新优化，以实现低功耗和延迟时间的优势。

锁存式感应放大器或再生式比较器以其低功耗和快速决策时间而著称，同时保持可接受的精度[1–4]。低功耗通过降低静态漏电流实现，其强正反馈提供了极快的响应速度。通常，锁存式比较器在由时钟信号启动的两个阶段中运行。第一阶段称为复位阶段，施加输入信号且正反馈被禁用；第二阶段称为再生阶段，正反馈开始工作，输出达到其最终值。

本文提出了一种新的高分辨率低功耗双尾锁存式比较器。该提出的比较器在中等频率下功耗仅为几纳瓦，适用于能源受限的应用场合，如植入式生物医学设备。本文结构如下：下一节介绍锁存比较器的常见结构；第3节描述了提出的比较器；第4节讨论并分析了所提出比较器的延迟时间；第5节给出了仿真结果，包括所提出的电路与传统双尾锁存比较器在功耗、延迟时间和反冲噪声方面的性能比较。最后，第6节给出结论。

2 锁存比较器

图1显示了一个传统锁存比较器[5, 6, 2]。该比较器工作于两个阶段：复位阶段（当时钟为低电平时）和再生阶段（当时钟为高电平时）。在复位阶段，M8和M9导通，将输出（V⁺out 和 Vo⁻ut）拉至VDD。此外，电流源M1关闭，从而消除了从VDD到地的静态电流（除可忽略的漏电流外）。在再生阶段，电流源导通，输出电压开始以与其相应输入成比例的不同速度向地放电。放电将持续，直到M6或M7的栅源电压降至M6;7的阈值电压以下，从而使其中一个导通。随后，锁存器开始工作，迫使一个输出达到VDD，另一个输出则达到地。

尽管功耗低且速度快，传统锁存比较器仍存在一些缺点。首先，晶体管的堆叠需要更高的裕压，以确保所有晶体管正常工作，这在极低电压和亚阈值应用中可能存在问题。其次，由于差分输入晶体管的漏极处存在较大的电压摆幅，导致反冲噪声相对较大[7, 6]。最后，锁存器的电流与输入晶体管共用，因此提高速度需增加电流，从而增加了功耗。因此，存在速度‐功耗权衡。

作为一种替代方案，双尾锁存比较器在[2]和[8]中被提出，如图2所示。双尾锁存比较器由两个阶段组成，并具有两个独立的电流尾。第一级采用小电流以实现低失调。第二级是带有大电流的锁存器，以提供短延迟时间。与锁存式比较器类似，双尾锁存比较器工作于两个阶段。在复位阶段（即当时钟为低电平时），两级的电流源M5和M12被关断，确保无静态功耗。

在第一阶段，M3和M4导通，将V⁺out1和Vo⁻ut1拉至VDD。因此，M6和M7被开启，输出（即V⁺out和V⁻out）被复位到地。

在再生阶段（即时钟为高电平时），电流源导通，而M3和M4关闭。因此，V⁺out1和V⁻out1将以与其相应输入成比例的不同速度放电。当第一级的某一输出降至M6或M7的阈值电压以下时，中间晶体管（M6或M7）将关闭。锁存器的正反馈开始[9]，迫使一个输出达到VDD，另一个输出则达到地。

该比较器的堆叠晶体管较少，因此可以在低电源电压下工作。此外，M6和M7在输入和输出之间提供了额外的屏蔽，降低了反冲噪声。

3 提出的比较器

图3显示了提出的比较器的结构。该比较器由三级组成。第一级是具有两对差分输入和二极管连接负载的差分放大器。其中一对差分输入为In⁺和In⁻，另一对是Vo⁺ut1和Vo⁻ut1，它们来自第二级的反馈。在第二级中，与传统的双尾锁存比较器相比，增加了两个额外的晶体管M20和M21（以灰色表示）。它们分别与第二级的输入晶体管M1和M2并联。来自第一级的Vb1和Vb2被施加到M21和M20的栅极上。M20和M21与第一级共同提供正反馈，从而提高分辨率。最后，最后一级是一个由两个背对背反相器和NMOS中间晶体管（即M6和M7）组成的快速锁存器。

类似于传统的双尾锁存比较器，该电路工作在两个阶段。在复位阶段（当时钟为低电平时），除了第一级的电流源M5和M12外，M19也被关断，因此第一级不消耗任何静态功耗。此外，Vb1和Vb2连接在一起以消除将记忆从一个决策周期转移到下一个决策周期。在再生阶段（当时钟为高电平时），M17和M18导通。Vb1和Vb2开始放电。在此阶段开始时，M17和M18具有相等的电导，因为它们的栅极电压V⁻out1和V⁺out1相同且等于VDD。然而，一段时间后，它们的电导将随对应的栅极电压成比例变化。因此，Vb1和Vb2之间的差异增大。该差异将在M20和M21中被放大。因此，V⁺out1和V⁻out1的放电速率差异将被进一步加剧。这导致更高的分辨率和更快的决策。

在再生阶段，Vb1和Vb2的电压持续下降，直到锁存器开始工作。需要注意的是，在晶体管尺寸相等的情况下，由于M17和M18的体效应，M17;18的阈值电压高于M6;7的阈值电压。这确保了当V⁺out1和V⁻out1降至中间NMOS晶体管的阈值电压以下时，M18和M17已经关断。因此，在再生阶段的空闲时间内消除了静态电流。因此，第一级仅在再生阶段的短暂部分消耗功率。

为了说明该比较器的性能是如何提升的，考虑当In⁺大于In⁻的情况。在再生阶段开始时，V⁺out1和V⁻out1从VDD向地放电。然而V⁺out1比V⁻out1放电更快。这导致在每一时刻V⁺out1都小于V⁻out1。同时，在第一级中，Vb1和Vb2根据其相应输入以不同速率放电。由于在右支路中，In⁺和V⁻out1均大于左支路中的In⁻和V⁺out1，因此Vb1比Vb2放电更快。结果，Vb1<Vb2。因此，在第二级中，V⁺out1受到Vb2(Vb1)的影响。

4 延迟时间分析

根据图4所示的提出比较器的瞬态行为，延迟时间可以分解为两部分。在第一部分（tsw）期间，输出电容以负指数形式呈指数充电至某一特定值。在第二部分（tlatch）中，正反馈启动，输出以正指数形式迅速变化，直至达到其最终值（图4(a)）。延迟时间可表示为

$$ t_{delay} = t_{sw} + t_{latch} \quad (1) $$

其中，tsw被视为从时钟上升沿到锁存器开始工作之间的时间间隔。如果在tsw时刻输出端的差分电压为ΔV₀，则锁存器的传播延迟时间为（见[1]）

$$ t_{latch} = \tau \ln \frac{V_{DD}}{2\Delta V_0} \quad (2) $$

其中τ是锁存器的时间常数，等于R_out C_L，而R_out是锁存器的输出电阻。

根据公式(2)，传播延迟时间与ΔV₀的倒数成对数关系。关于锁存级开始时间存在不同的观点。在一些文章中，它被认为是锁存器中交叉耦合反相器的n沟道晶体管（即M8和M9）的输出之一达到阈值电压的时刻[9, 4]。然而，在中等和弱反型区，这一假设似乎不够准确。考虑到亚阈值行为[10,11]，正反馈的起始时间被定义为锁存级中某一反相器内的p型和n型沟道晶体管的漏极电流相等的时刻。这就是交叉耦合反相器的切换阈值。

图4(b)展示了锁存级中背对背反相器的漏极电流。在再生阶段，即时钟信号为高电平时，M12导通，且I12在M10和M11之间均分（I10=等于I11）。由于M8和M9在此阶段开始时处于关断状态，M10和M11的漏极电流分为两路：一路流向负载电容（CL），另一路流向中间晶体管M6;7。随着V⁺out1和V⁻out1的降低，M6;7的栅源电压从VDD逐渐下降至地。因此，M6;7的漏极电流随之减小，直至完全关断。与此同时，负载电容开始充电，直到其中一个晶体管M8或M9导通。锁存器开始再生，连接在导通晶体管漏极上的负载电容放电至地，而连接在关断晶体管上的负载电容则充电至VDD。

我们的仿真结果表明，在锁存器中的交叉耦合反相器的p沟道和n沟道晶体管的电流相等时，输出电压的二阶导数近似为零。这可以通过比较图4(b)中的电流和图4(c)中输出电压的一阶导数来确认。大约在= 35.004 μs，即点(a)，当电流I9和I11相等时，一阶导数的梯度（或二阶导数）变为零。该结果表明延迟时间由两部分组成。此外，电路的行为在点(a)处发生变化。

本文中，tsw被假定为M9(M8)和M11(M10)的漏极电流相等的时刻（图4(b)）。此时，M7(M6)的亚阈值电流被忽略。

在In⁺大于In⁻的情况下，可通过将M9和M11的亚阈值漏极电流相等来计算t＝tsw时刻V⁺out的相应电压（即Vsw）。MOSFET的亚阈值电流由以下公式给出

$$ I_{sub} = I_0 \exp \left( \frac{V_{GS} - V_{Th}}{nV_T} \right) \quad (3) $$

其中，V_T是热电压（300K时为≈26毫伏），V_Th是阈值电压，n是亚阈值斜率[10,11]。此外，当VGS等于阈值电压时，I0是晶体管的漏极电流。对于NMOS晶体管，I0由（见[10]）得出

$$ I_0 = 2\mu_n c_{ox} \frac{W}{L} nV^2_T \quad (4) $$

其中μ_n为电子迁移率，c_ox为单位面积栅氧化层电容。对于PMOS晶体管，式(4)中的μ_n应替换为空穴迁移率μ_p。通过考虑I11 ≈ I12 / 2并将I9与I11, Vsw相等，可计算出

$$ V_{sw} = V_{Thn} + nV_T \ln \frac{I_{12}}{2I_0(9)} $$

$$ I_0(9) = 2\mu_n c_{ox} \frac{W}{L}_9 nV^2_T \quad (5) $$

在公式(5)中，Vsw的第一部分是背对背反相器的n沟道晶体管的阈值电压，第二部分是一个对数函数，其输入在亚阈值区始终小于1。因此，第二部分为负电压。所以，I12与I0(9)的比值越小，比较器的切换电压就越低。这可以通过减小(W/L)12/(W/L)9的比值得到。

为了计算ΔV₀，需结合大信号和小信号的差分输出电流表达式

$$ \Delta I_{out} = I_{10} - I_{11} $$
$$ = I_0(10;11) \left[ \exp \left( \frac{V_{GS10} - V_{Thp}}{nV_T} \right) - \exp \left( \frac{V_{GS11} - V_{Thp}}{nV_T} \right) \right] $$
$$ = g_{m6}V⁺ {out1} - g {m7}V⁻_{out1} \quad (6) $$

其中V_Thp是M10;11的阈值电压。最后，通过在t=tsw时求解式(6)，并将V⁺out和V⁻out分别设为Vsw和(Vsw - ΔV₀)来计算ΔV₀。

$$ \Delta V_0 = nV_T \ln \left[ \frac{g_{m6;7}\Delta V_{out1} \exp \left( \frac{V_{Thp} + V_{Thn} - V_{DD}}{nV_T} \right)}{\frac{I_{12}}{2I_0(8;9)} I_0(10;11)} + 1 \right] \quad (7) $$

其中ΔV_out1定义为V⁺out1 - V⁻out1。上述方程表明，ΔV₀与中间晶体管M6和M7的跨导、ΔV_out1以及I12呈对数关系。由于该比较器中的ΔV_out1受到两对晶体管的影响，因此相较于传统双尾锁存比较器更大。这导致ΔV₀更大，从而使得t_latch更短。

5 仿真结果

提出的比较器在0.18μm CMOS技术下设计并进行仿真，温度为27°C。在上一节中，ΔV₀通过公式（7）进行了理论计算。为了验证这些分析与仿真结果一致，ΔV₀（由公式（7）提取）与仿真结果进行了对比。图5展示了ΔV₀随差分输入电压变化的计算和仿真结果。电源电压和共模电压分别为0.5和0.25伏特。在公式（7）中，假设M6和M7工作在饱和区。由于电源电压为0.5伏特，M6和M7工作在亚阈值区（M6和M7的阈值电压约为0.52伏特）。因此，为了计算g_m6;7，使用了以下方程，该方程表示MOSFET在饱和区和亚阈值区的跨导。

$$ g_m = \frac{\partial I_{sub}}{\partial V_{GS}} = \frac{I_0}{nV_T} \exp \left( \frac{V_{GS} - V_{Th}}{nV_T} \right) \quad (8) $$

要计算亚阈值斜率，首先从仿真中提取亚阈值斜率因子（S）。通过dVGS/d(logId)[11]可获得S。然后，根据以下公式计算亚阈值斜率（见[11]）

$$ n = \frac{V_T \ln(10)}{S} \quad (9) $$

此外，ΔV_out1在公式（7）中是通过仿真作为输入电压的函数进行测量的。最后，I12由公式（3）计算得出，其中VGS被视为VDD。注意，在锁存阶段开始时，V_GS6;7和V_SG12等于VDD。此外，V_DS6;7和V_SD12接近于零。因此，对于大于V_Th的电源电压，M6, M7和M12不再工作在亚阈值区，而应使用强反型的等效方程，取代公式（8）和（3）。如图5所示，计算结果与仿真结果，特别是对于低输入电压的情况，具有良好的一致性。

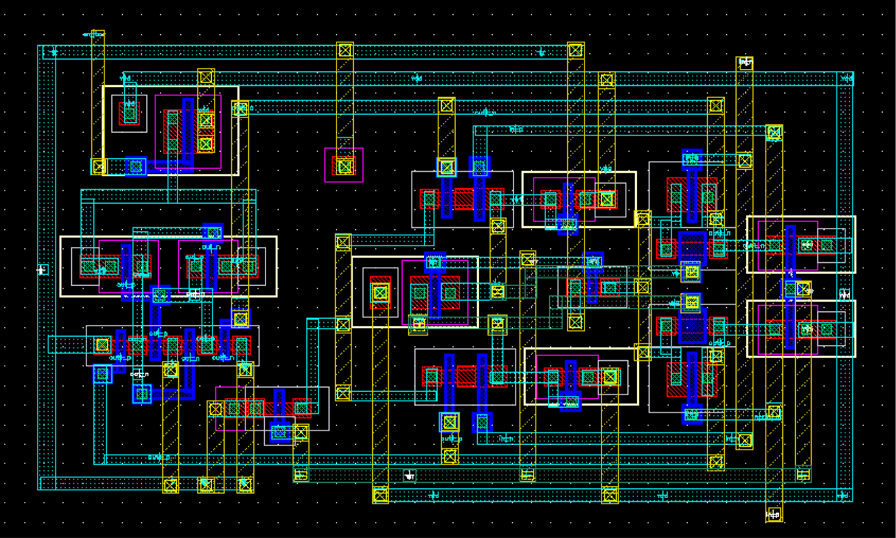
为了展示提出的比较器性能的提升，在0.18μm CMOS技术下对传统双尾锁存比较器在27°C温度和100kHz时钟频率下进行了仿真。在两个比较器中，锁存级晶体管采用相同的尺寸。其他晶体管经过调整，以获得在VDD= 0.6V和Vcm= 0.35V时相等的输入参考失调标准偏差7.5mV。图6显示了该比较器与传统比较器瞬态行为的仿真结果对比。在提出的比较器中，通过降低t_sw并增加ΔV₀来减少总延迟时间。图7显示了提出比较器的版图。面积约为11μm×19μm。图8展示了作为电源电压函数的提出比较器和传统双尾锁存比较器的布局后仿真功耗结果。在此仿真中，时钟频率为100kHz。电源电压从400毫伏至1伏特变化，差分输入电压设为5毫伏。该仿真在两种不同的共模输入电压下进行。实线表示共模电压位于电源电压中间时的结果，虚线表示共模电压比VDD/2高50毫伏时的结果。

当共模输入电压为VDD/2时，传统的双尾锁存比较器的功耗明显高于提出的电路。例如，在VDD= 0.6V时，传统比较器的功耗为4.49纳瓦，而提出的电路仅为1.56纳瓦（降低65%）；或者在最坏情况下，当电源电压为700毫伏时，传统比较器的功耗增加到5纳瓦，是提出电路功耗的2.63倍。当共模输入电压增加至VDD/2＋50毫伏时，传统比较器的功耗有所降低，但在580至770毫伏的电源电压范围内，提出的比较器仍然具有更低的功耗。

图9显示了在不同电源电压下的版图后仿真延迟时间。在此仿真中，延迟定义为时钟信号上升沿与输出信号穿过电源电压中间值时刻之间的时间差。相同的定义用于在后续仿真中获得延迟时间。如图所示，当电源电压从400毫伏增加到1伏特时，两个电路的延迟均减小。通常情况下，当Vcm = VDD/2时，提出的比较器相比传统比较器具有更短的延迟时间。此外，在Vcm = VDD/2＋50毫伏时，提出的比较器在470毫伏电源电压下能更快地做出判决。

根据图8、9所示的仿真结果，提出的比较器相比传统比较器在功耗和延迟方面有所改善。提出的电路中的附加反馈减少了延迟时间，从而显著降低了瞬态时间。动态比较器的峰值功耗出现在瞬态期间。在固定电流源中，瞬态时间的减少会导致功耗降低。然而，当电源电压增加时，由于附加级的存在，提出比较器的总电流增加，因此功耗增加（见图8中的蓝色曲线）。

尽管锁存比较器具有低功耗和快速判决的优点，但它们通常会受到反冲噪声的影响[7, 12, 6, 13]。在锁存式比较器中，内部节点的大电压变化会耦合到输入端，从而干扰输入电压，这种现象称为反冲噪声。反冲噪声可能导致显著的动态失调，甚至使比较器输出错误，降低分辨率[12, 14]。为了评估反冲噪声，前一级电路采用戴维南等效电阻建模[15]此处视为8 kΩ（图10）。

为了确保考虑反冲噪声的最坏情况，仿真在两种不同情况下进行：首先仿真在200MHz时钟频率和1V电源电压（Vcm = 500mV）下进行。图11(a)显示了差分输入电压，从300mV变化到-10毫伏，在t=50ns时。由于反冲噪声的影响，差分输入电压在时钟信号的任何跳变沿都会产生微小波动。在t=50ns之前，传统比较器的输入电压在时钟信号的下降沿处峰值为7.6毫伏（见图11(b)）。提出的比较器对应的值为5.9毫伏。在t=50ns之后，当差分输入电压为-10毫伏时，反冲噪声的影响几乎可以忽略不计，因为在传统比较器和提出的比较器中其峰值分别为0.6毫伏和0.8毫伏。

第二次仿真在20MHz时钟频率和600mV电源电压下进行（图12(a)）。如布局后仿真结果所示，在这种情况下，反冲噪声的影响与1V电源电压的情况相比要小得多。当差分输入电压为300mV时，传统双尾锁存比较器中反冲噪声的峰值为0.34毫伏，提出的比较器中为0.31毫伏（见图12(c)）。在t=0.5μs后，当差分输入电压等于-10 mV时，两个电路中由反冲噪声引起的峰值都很小（见图12(b)）。

介绍了多种降低反冲噪声的方法。最有效的方法是在比较器前使用预放大器，以避免从输出到输入的直接通路[16, 17]。然而，额外的预放大器会增加静态功耗。另一种降低反冲噪声的方法是在再生阶段通过使用MOS开关将输入晶体管的漏极与输出节点隔离[18, 15, 17]。或者，可以在再生阶段断开输入[19]。在[15, 12, 14]中采用了中和技术。该技术在每个输入晶体管的漏极与另一个输入晶体管的栅极之间添加一对交叉耦合电容器。这些电容器的作用能有效减小反冲噪声。通常，电容器的取值选择与输入晶体管的栅-漏电容相等[12]。在[15]和[14]中，采用两个n沟道晶体管作为中和电容。提出的比较器得益于自中和技术，因为存在一条从漏极到每个输入晶体管的漏极连接到另一个晶体管的栅极。例如，将M1和M2作为主要的输入晶体管，M1（M2）的漏极通过M20（M21）和M16（M15）的栅-漏电容连接到M2（M1）的栅极。与具有相同尺寸输入晶体管的传统锁存比较器相比，这降低了反冲噪声的影响。

在400次运行中进行考虑工艺和失配偏差的蒙特卡洛仿真，得到提出的比较器的失调电压标准偏差为7.57毫伏（见图13）。我们确认，在最坏情况下，传统比较器也获得了相似的标准偏差（数据未显示）。在这些仿真中，VDD、Vcm和fClk分别为0.6、0.35伏特和100千赫兹。为了估计输入参考失调，将一个在2毫秒内从-30到30毫伏变化的斜坡信号作为差分输入电压施加。当比较器输出发生从0到1的跳变时，失调电压被认为等于差分输入电压。

通常情况下，失调电压取决于晶体管尺寸。使用较小的晶体管会导致更低的功耗或更快的电路。同时，较小的晶体管会导致更高的失调电压。需要对由失配误差引起的失调电压进行分析，以验证或改进设计。通过使用蒙特卡洛仿真表明，我们降低功耗和延迟时间的尝试并未使失调电压恶化。

图14(a, b)展示了所提出的比较器在功耗和传播延迟方面的工艺角仿真结果。如图所示，在FF角下，提出的比较器具有最高的功耗和最短的延迟时间。此外，在SS角下，其功耗最低且速度最慢。

图15(a, b)描述了所提及比较器在输入共模电压变化下的布局后仿真结果，包括功耗和延迟时间。在此仿真中，时钟频率为100千赫兹，电源电压为0.6伏特，共模电压从0.2至0.59伏特变化。与传统比较器相比，提出的比较器的功耗和延迟时间受输入共模电压变化的影响较小。图16(a, b)显示了在工艺偏差条件下进行400次运行的蒙特卡洛仿真结果，针对功耗和延迟时间。工艺偏差导致功耗的标准偏差为29.94皮瓦。这表明功耗受工艺偏差的影响不显著。

功耗和(b) 延迟随共模电压的变化（VDD=600毫伏，ΔVin =5毫伏，fClk = 100千赫兹）)

表1总结了该比较器与[7, 20]和[9]中提出的电路设计的规格对比。所有电路均包含锁存结构。由于大多数电路在功耗和速度之间存在权衡，因此还计算了功耗延迟积(PDP)和每次转换能耗，以实现更全面的比较。

比较器特性	[20]	[7]	[9]	提出的
拓扑结构	双尾锁存比较器	带自适应电源控制电路	双尾锁存比较器	双尾锁存式比较器
技术	600纳米	65纳米	0.18微米	0.18微米
电源电压 (V)	5	0.8	0.8	0.6
反冲噪声 (mV)	–	3–6.2	13	0.3
延迟时间	5毫伏输入时为5皮秒	100微伏输入电压时为1.17纳秒	670皮秒（5毫伏输入）	5毫伏输入时为8.3纳秒
总平均功率	2.7微瓦在100千赫兹	191.2纳瓦在15兆赫	–	1.56纳瓦在100千赫兹
PDP（飞焦）	0.0135	0.2	–	0.0172
每次转换能量 (pJ)	0.027	0.0126	0.24	0.0156
输入参考偏移电压 (mV)	0.053	–	7.8	7.57

6 结论

本文提出了一种新的超低功耗双尾锁存比较器。该提出的比较器适用于400毫伏至1伏特之间的电源电压。为了检验所提出电路的性能，将其结果与传统双尾锁存比较器进行了比较。此外，通过解析方法获得了初始输出电压对设计参数的依赖关系，这有助于优化所设计的电路。仿真结果显示，当共模电压为电源电压的一半时，功耗显著降低。在600毫伏电源电压下，与传统比较器相比，提出的比较器功耗降低了65.2%，同时输入参考失调为7.5毫伏。由于具有自中和特性，在0.6伏电源电压和20兆赫时钟频率下，提出的比较器反冲噪声比传统比较器减少了11.76%。当电源电压为1伏特、时钟频率为200兆赫兹时，反冲噪声进一步降低了22%。随着共模电压的增加，提出的比较器的功耗没有明显变化。然而，尽管传统比较器的功耗显著降低，但仍与提出的电路相当。