POJ 2976最简单的 01分数规划

最新推荐文章于 2021-03-23 20:24:54 发布

原创最新推荐文章于 2021-03-23 20:24:54 发布 · 203 阅读

0 ·

CC 4.0 BY-SA版权

分数规划专栏收录该内容

3 篇文章

订阅专栏

本文介绍了解决特定数学问题的两种算法——二分法和Dinkelbach算法，并通过示例代码详细展示了这两种算法的实现过程。二分法通过不断缩小解的空间来逼近最优解，而Dinkelbach算法则通过迭代更新初始解逐步优化。

题目：给出n个a和b，让选出n-k个使得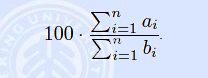这里写图片描述最大。

二分法（二分一个mid看是否存在这样的一组解，不断缩小区间逼近最优值）

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long ll;
#define eps 1e-6
#define inf 1e12
const int maxn=1010;
int n,k;
int a[maxn],b[maxn];
double y[maxn];
bool check(double x)
{
    for(int i=1;i<=n;i++)
        y[i]=a[i]-b[i]*x;
    sort(y+1,y+n+1);
    double sum=0;
    for(int i=1;i<=k;i++)
        sum+=y[n-i+1];
    return sum>0;
}

void solve()
{
    double l=0,r=inf;
    while(r-l>eps)
    {
        double mid=(l+r)/2;
        if(check(mid))
            l=mid;
        else r=mid;
    }
    printf("%.0f\n",l*100.0);
}

int main()
{
    while(~scanf("%d%d",&n,&k))
    {
        if(n+k==0) break;
        k=n-k;
        for(int i=1;i<=n;i++)
            scanf("%d",&a[i]);
        for(int i=1;i<=n;i++)
            scanf("%d",&b[i]);
        solve();
    }
    return 0;
}

Dinkelbach算法（本质是一种迭代算法，基于这样的思想：不去二分答案，而是先随便给定一个答案，然后根据更优的解不断移动答案，逼近最优解。理论上它比二分快些。在这个算法中，一般将ans初始化为0）

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long ll;
#define eps 1e-6
#define inf 1e12
const int maxn=1010;
struct node{
    int a,b;
    double y;
}s[maxn];
bool cmp(const node &a,const node &b)
{
    return a.y>b.y;
}
int n,k;
double Dinkelbach()
{
    double ans=0,x=0,U,D;
    while(1)
    {
        x=ans;
        for(int i=1;i<=n;i++)
            s[i].y=s[i].a-s[i].b*x;
        sort(s+1,s+n+1,cmp);
        U=D=0;
        for(int i=1;i<=k;i++)
        {
            U+=1.0*s[i].a;
            D+=1.0*s[i].b;
        }
        ans=U/D;
        if(fabs(ans-x)<eps)
            return ans;
    }
}

int main()
{
    while(~scanf("%d%d",&n,&k))
    {
        if(n+k==0) break;
        k=n-k;
        for(int i=1;i<=n;i++)
            scanf("%d",&s[i].a);
        for(int i=1;i<=n;i++)
            scanf("%d",&s[i].b);
        printf("%.0f\n",Dinkelbach()*100.0);
    }
    return 0;
}