CSP-J系列【2024】P11229 [CSP-J 2024] 小木棍题解

题目描述

小 S 喜欢收集小木棍。在收集了 n 根长度相等的小木棍之后，他闲来无事，便用它们拼起了数字。用小木棍拼每种数字的方法如下图所示。

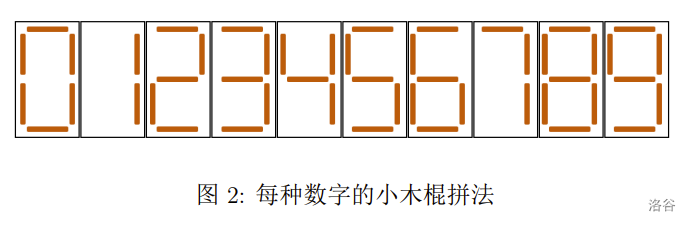
现在小 S 希望拼出一个正整数，满足如下条件：

• 拼出这个数恰好使用 n 根小木棍；
• 拼出的数没有前导 0；
• 在满足以上两个条件的前提下，这个数尽可能小。

小 S 想知道这个数是多少，可 n 很大，把木棍整理清楚就把小 S 折腾坏了，所以你需要帮他解决这个问题。如果不存在正整数满足以上条件，你需要输出 −1 进行报告。

输入格式

本题有多组测试数据。

输入的第一行包含一个正整数 T，表示数据组数。

接下来包含 T 组数据，每组数据的格式如下：

一行包含一个整数 n，表示木棍数。

输出格式

对于每组数据：输出一行，如果存在满足题意的正整数，输出这个数；否则输出 −1。

输入输出样例

输入 #1复制

5
1
2
3
6
18

输出 #1复制

-1
1
7
6
208

说明/提示

【样例 1 解释】

• 对于第一组测试数据，不存在任何一个正整数可以使用恰好一根小木棍摆出，故输出 −1。
• 对于第四组测试数据，注意 0 并不是一个满足要求的方案。摆出 9、41 以及 111 都恰好需要 6 根小木棍，但它们不是摆出的数最小的方案。
• 对于第五组测试数据，摆出 208 需要 5+6+7=18 根小木棍。可以证明摆出任何一个小于 208 的正整数需要的小木棍数都不是 18。注意尽管拼出 006 也需要 18 根小木棍，但因为这个数有前导零，因此并不是一个满足要求的方案。

【数据范围】</