LCA：倍增

最新推荐文章于 2024-10-10 23:56:11 发布

原创最新推荐文章于 2024-10-10 23:56:11 发布 · 371 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#C++ #图论

博客介绍了LCA（最近公共祖先）的概念，即在树中两个节点的最近公共祖先。还阐述了LCA的几种解决方法，包括向上标记法、倍增法和树链剖分，分析了各方法的时间复杂度，并给出了部分代码示例。

lca

先给张图（声明luogu版权）
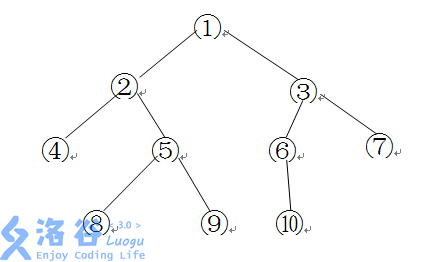
在这里插入图片描述
lca是什么呢，就是在一棵树里，两个节点的最近公共祖先
比如说，在上图中，4和5的lca就是2，8和10的lca就是1（很好理解对吗）

lca主要有这样一些解决的方法

向上标记法
顾名思义，从x向上走，走到根节点，标记。从y向上走，走到根节点，标记，第一次遇到标记过的点时，就是lca(x,y)
但是…时间上…卡一卡可以卡到O(n)
还是太慢了

倍增法

一个非常实用的算法
设f(x,k)为x的2^k辈祖先，显然f(x,0) is x’s father
另外，f(x,k)=f(f(x,k-1),k-1)
这里可以使用一个dfs进行预处理，复杂度为O(n log n)

inline void dfs(int u,int fa){
	f[u][0]=fa;
	depth[u]=depth[fa]+1;
	for(int i=1;(1<<i)<=depth[u];i++) f[u][i]=f[f[u][i-1]][i-1];
	for(int i=head[u];~i;i=e[i].next) if(e[i].to!=fa)dfs(e[i].to,u);
}

接下来就是查询，是一个在线的操作，每次查询复杂度为log(n)
伪代码：

first let depth[x]>=depth[y]
second let depth[x]=depth[y]
if x=y print x
else push x,y up to there LCA's sons
print x's father
版权归属：kkksc03&&chen_zhe

真代码：

inline int lca(int x,int y){
	if(depth[x]<depth[y]) swap(x,y);
	while(depth[x]>depth[y]) x=f[x][lg[depth[x]-depth[y]]-1];
	if(x==y) return x;
	_Rep(k,lg[depth[x]]-1,0) if(f[x][k]!=f[y][k]) x=f[x][k],y=f[y][k];
	return f[x][0];
}

这里因为有查询log的操作，这里是加了一个常数优化

Rep(i,1,n) lg[i]=lg[i-1]+(1<<lg[i-1]==i);

这里应该挺好理解的，就不多说了

完整代码 luogu LCA模板

# include <cstdio>
# include <algorithm>
# include <cstring>
# include <cmath>
# include <climits>
# include <iostream>
# include <cstring>
# include <queue>
# include <vector>
# include <set>
# include <map>
# include <cstdlib>
# include <stack>
# include <ctime>
using namespace std;

# define Rep(i,a,b) for(int i=a;i<=b;i++)
# define _Rep(i,a,b) for(int i=a;i>=b;i--)
# define mct(a,b) memset(a,b,sizeof(a))
# define gc getchar()
typedef long long ll;
const int N=5e5+5;
const int inf=0x7fffffff;
inline int read(){
	int s=0,w=1;
	char c=gc;
	while(c<'0'||c>'9'){if(c=='-')w=-1;c=gc;}
	while(c>='0'&&c<='9')s=s*10+c-'0',c=gc;
	return s*w;
}
int n,m,s;
int head[N],cnt,lg[N],f[N][20],depth[N];
struct Edge{
	int to,next;
}e[N<<1];

inline void add(int x,int y){
	e[++cnt]=(Edge){y,head[x]},head[x]=cnt;
}

inline void dfs(int u,int fa){
	f[u][0]=fa;
	depth[u]=depth[fa]+1;
	for(int i=1;(1<<i)<=depth[u];i++) f[u][i]=f[f[u][i-1]][i-1];
	for(int i=head[u];~i;i=e[i].next) if(e[i].to!=fa)dfs(e[i].to,u);
}

inline int lca(int x,int y){
	if(depth[x]<depth[y]) swap(x,y);
	while(depth[x]>depth[y]) x=f[x][lg[depth[x]-depth[y]]-1];
	if(x==y) return x;
	_Rep(k,lg[depth[x]]-1,0) if(f[x][k]!=f[y][k]) x=f[x][k],y=f[y][k];
	return f[x][0];
}

int main()
{
	mct(head,-1);
	n=read(),m=read(),s=read();
	Rep(i,1,n-1){
		int u=read(),v=read();
		add(u,v);
		add(v,u);
	}
	
	dfs(s,0);
	
	Rep(i,1,n) lg[i]=lg[i-1]+(1<<lg[i-1]==i);
	
	Rep(i,1,m){
		int u=read(),v=read();
		printf("%d\n",lca(u,v));
	}
	return 0;
}