低成本SDR实现纳秒级飞机信号TOA估计

使用低成本软件定义无线电接收机实现飞机信号的纳秒级到达时间估计

摘要

飞机和无人机信号的精确到达时间（TOA）估计对于多种应用至关重要，包括飞机/无人机跟踪、空中交通数据验证和自定位。本文的研究重点是可在低成本软件定义无线电（SDR）接收机上运行的到达时间估计方法，这类接收机广泛部署于模式S / 广播式自动相关监视的众包传感器网络（如OpenSky网络）。我们实验评估了基于与重建的消息模板进行互相关的经典到达时间估计方法，发现这些方法对于此类信号并非最优。我们提出了两种替代方法，在使用低成本SDR接收机捕获的真实世界模式S / 广播式自动相关监视信号上表现出更优的性能。其中最佳方法达到1.5纳秒的标准偏差误差。

引言

飞机和无人驾驶航空器持续发射无线信号，用于空中交通管制和防撞。这些信号要么作为对二次监视雷达（SSR）询问的应答而发送，要么自动以周期性方式发送（广播式自动相关监视）。这两类信号均通过所谓的模式S 数据链[12]在1090兆赫无线电频率上传输。

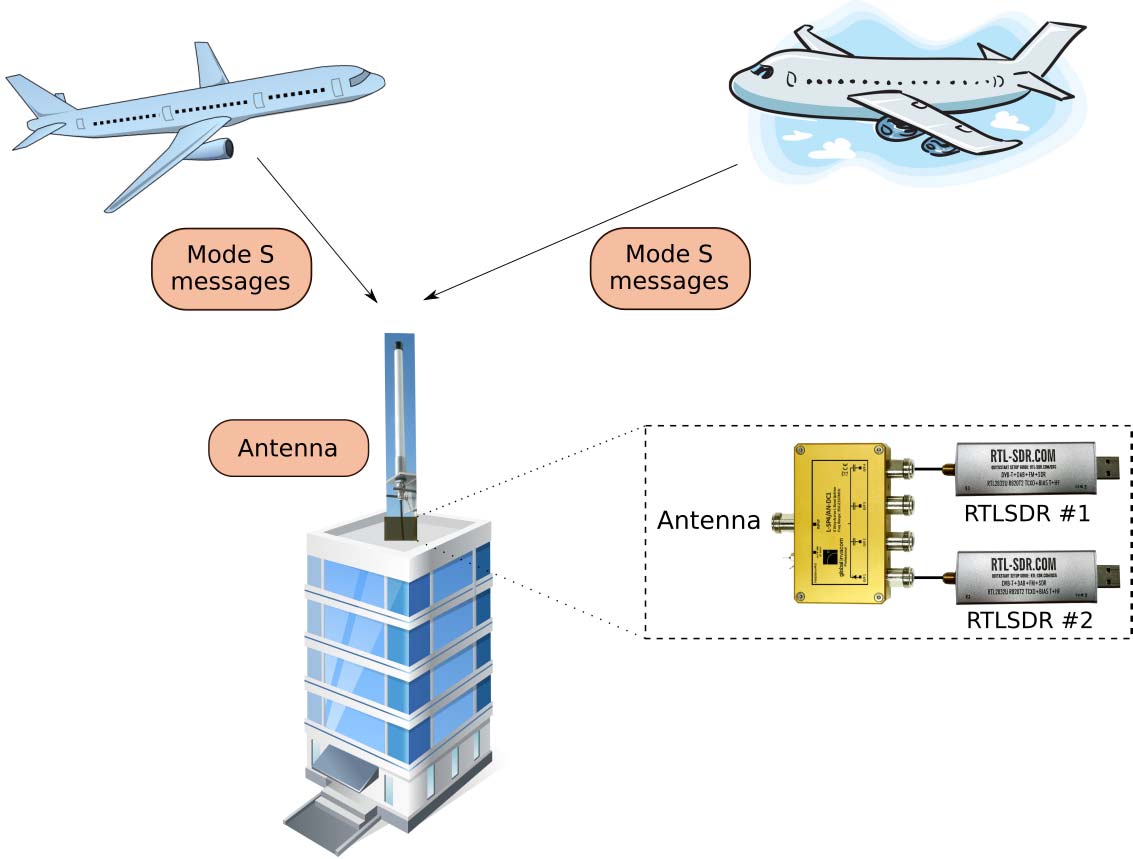
在过去的几年中，出现了一些传感器网络项目，这些项目利用大量低成本的软件定义无线电（SDR）接收机（例如 OpenSky网络[20], Flightaware[5], Flightradar24[6]以及其他许多系统）来收集上述信号。这些传感器网络可利用模式S信号的到达时间（TOA）实现多种应用，包括飞机定位 [20, 22], 空中交通数据验证[13, 16, 17, 19, 21], 以及自定位[15]。

在这些应用中，一组协同工作的接收机本地测量到达信号的到达时间（TOA），然后将这些数据发送到中央计算服务器。通过对同一信号在不同接收机处到达时间（TOA）的联合处理，中央服务器能够估计发射机的位置、接收机的位置，或信号发射的精确时间。

这些应用的精度在很大程度上取决于到达时间估计的精度，为了将定位精度估计到几米以内，必须以纳秒级精度来估计到达时间。本工作的目标是提供一种针对S模式信号的到达时间估计方法，即使使用诸如广泛应用的低成本软件定义无线电接收机，也能实现纳秒级精度。

RTL-SDR 软件狗 [3]。我们表明，在S模式信号的特定背景下，基于与重建信号模板进行互相关来实现到达时间估计的现有方法并非最优。事实上，规范对数据包内每个符号的形状和位置所允许的宽松容差范围（最大达 ± 50 ns）会对接收机处整个数据包波形的重建引入不确定性。

我们提出了两种替代方法，可在提高精度的同时降低计算负载。我们在真实世界信号迹线上测试了不同的到达时间估计变体，这些信号迹线是使用RTL-SDR捕获的，而 RTL-SDR目前是市场上最便宜的软件定义无线电设备，被众包传感器网络广泛使用。我们的结果表明，最优的提出的方法可实现1.5纳秒的标准偏差误差的到达时间估计。我们进一步发现RTL-SDR设备的有限动态范围（小于50 dB，采用8位模数转换器（ADC）和固定的自动增益控制器（AGC））是主要的性能瓶颈，并证明对于未因设备有限动态范围而发生削波的信号，可实现亚纳秒精度。

2 背景

本节介绍了我们依赖的飞机信号的背景知识，以及经典到达时间估计方法的局限性。

2.1 模式S信号格式

接下来我们简要回顾飞机在1090 MHz信道上传输的二次雷达模式S [18]应答以及ADS-B消息的物理层格式。这两种数据包格式均由一个持续时间为8 μs的前导码和一个长度为112比特或56比特（仅适用于其他二次雷达模式S应答）的有效载荷组成，传输速率为1 Mbps，总持续时间分别为120 μs或64μs。信息比特采用简单的二进制脉冲位置调制（BPPM）方式进行调制，如图1所示：符号周期 1 μs被划分为两个“码片”，每个码片为0.5 μs，其中高到低跳变和低到高跳变分别编码比特“1”和“0”。从图 1可以明显看出，BPPM调制产生两种不同持续时间的脉冲，此后分别记为“I型”和“II型”。I型脉冲的标称持续时间为一个码片周期，由比特序列“00”、“11”和“10”产生。前导码由四个I型脉冲组成。另一方面，II型脉冲的标称持续时间为两个码片周期，仅由“01”序列产生。平均而言，我们

对于112比特的有效载荷，预期大约有112/2= 56个I型脉冲和112/ 4= 28个II型脉冲。

然后，实值基带信号被调制到1090兆赫载波频率上并进行无线传输。在接收端，解码过程仅依赖于信号幅度，因为在 BPPM中，信号相位 不携带任何信息。

2.2 标准到达时间方法的局限性

在加性高斯白噪声（AWGN）信道中，到达时间估计的标准 “教科书”方法是使用相关滤波器[14]：将接收信号与对应于源信号的已知模板进行互相关，取互相关模最大的时间点作为到达时间估计。

相关方法依赖于以下假设：源信号可以在接收机处基于信号规范和有效载荷比特信息被非常精确地重建，其中有效载荷比特为p m。在此假设下，相关方法即为最大似然估计器（ MLE）[14]。然而，在实际的S模式信号情况下，该假设存在问题。事实上，标准规范允许数据包内每个脉冲的位置存在高达 ±50纳秒的抖动：对于解码过程而言，如此高的容差值实际上可忽略不计，但对于实现纳秒级精度的到达时间估计任务来说则不可忽略。至于每个脉冲的形状，脉冲的持续时间和上升时间允许有50纳秒的容差，下降时间甚至允许高达150纳秒的容差，同时脉冲幅度最多可变化2分贝（约60%）。如此宽松的容差范围会引入对源信号中脉冲形状和位置预测的不确定性。

考虑到S模式信号通常以高信噪比被接收，这种不确定性可能远超过加性噪声的影响。因此，采用已知数据包模板的基于相关的方案不再能保证是最优的，这促使人们寻求其他更精确的方法。

3 我们的到达时间估计方法

在本节中，我们首先描述基于解码后的有效载荷和接收信号样本进行到达时间估计的一般方法，然后介绍所测试的不同到达时间估算法。

3.1 信号采集架构

在软件领域，高精度到达时间估计过程可被视为在接收机内部可选调用的一个附加功能，且独立于主解码过程。因此，它可以在任何传统接收机之上实现，包括但不限于广泛采用的开源工具 dump1090[1]。所提出方案的整体框图如图2所示。传统接收机以采样率f s采集的复数同相和正交（IQ）样本流作为输入（对于RTL-SDR硬件，f s= 2.4 MHz）。传统接收机试图检测并解码接收到的数据包，若成功，则输出解码后的比特序列p m以及检测到的数据包的起始IQ样本指示。

记sm为对应整个数据包的复数IQ样本序列。该序列包含约300个样本，因为我们还在数据包前后额外选取了几个样本，以减轻边缘效应。样本向量sm和解码后的比特向量p m构成我们到达时间估计模块的输入。

3.2 提出的方法：相关脉冲和PeakPulse

下文将介绍两种专门为S模式信号设计的新型到达时间估计算法。对于一个通用的数据包 m，我们将其整个数据包（前导码和有效载荷）中的脉冲总数记为 Km。复数采样点输入向量 sm首先以因子 N进行上采样，并转换为向量 s′ m（有关上采样过程的综述，参见例如 [10]）。为了说明这一点，图3绘制了在实际追踪数据中找到的一个通用数据包对应的两个向量幅度片段，即 |sm| （上图）和 s′ m （下图）。

所提出算法的关键在于，每个数据包内第k个通用脉冲的实际时间位置ˆτ k是独立于其他脉冲进行估计的，无需重构整个数据包的模板。对于每个脉冲k ≥ 2，

我们计算各个偏移量 Δτ k def =ˆτ k −τ k，即相对于（估计的）第一个脉冲位置的估计脉冲位置与标称脉冲位置之间的差值。最后，对脉冲偏移进行平均以获得最终的到达时间估计：

ˆt= τˆ1+ 1 Km − 1 ÕKm k=2 Δτk (1)

两种提出的变体在获取单个脉冲位置估计的方法以及所考虑的脉冲类型上有所不同。在标记为相关脉冲的第一种变体中，每个脉冲位置通过将上采样向量s′ m与相应的标称脉冲形状进行脉冲级互相关来确定。最终平均中同时考虑了I型和II型脉冲。

在第二种变体中，标记为PeakPulse，通过简单地选取脉冲间隔内的局部最大值点来确定各个脉冲的位置，无需进行互相关操作。在此变体中仅考虑I型脉冲，而忽略II型脉冲。这是因为II型脉冲具有较低曲率，因此其局部峰值无法像I型脉冲那样可靠地识别。

4 评估方法

本节介绍我们如何评估新方法。首先，我们介绍用作比较参考的其他竞争方法。然后，我们展示使用商用低成本硬件的测试平台设置。最后，我们详细介绍在给定设置下用于实证评估到达时间测量方法精度的实验流程。

4.1 其他用于比较的方法

4.1.1 与完整数据包模板的互相关：CorrPacket

这是使用已知信号模板的标准互相关方法。对于每个数据包m，从解码比特p m重构完整数据包模板，然后与输入信号的幅度进行互相关。此处同样采用因子为N的上采样以实现亚采样精度。

在模板中，第k个脉冲位于标称时间τ k处。关于脉冲形状，我们测试了两种不同变体：“矩形”（R）和“平滑”（S）。这两个版本将分别表示为CorrPacket/R和CorrPacket/S。矩形脉冲的标称持续时间分别为Type-I脉冲0.5 μ秒和Type-II脉冲 1 μ 秒，且上升/下降时间为零。矩形脉冲掩码仅由“0”和“1” 值表示，因此与其他向量的乘法简化为元素选择，从而降低计算负载。“平滑”形状对应于低通滤波器的输出，其通带为 2.4兆赫——与RTL-SDR接收器的带宽相匹配——当输入信号为符合规范[11]、最小下降/上升时间为50纳秒的标称I型/II型 脉冲时。

4.1.2 基于 dump1090 的现有实现

我们还评估了开源工具 dump1090[1] 的可变性分支所报告的时间戳的精度。此外，我们在我们的迹线上测试了 Eichelberger 等人 在最近的 ACM SenSys’17 论文 [15] 中采用的方法，该方法同样基于 dump1090。代码检查显示，该方法基于与部分数据包模板 （包含前导码和四分之一有效载荷）在频域中实现的互相关，使用矩形脉冲和升采样因子 N= 25。

4.2 测试平台设置

实验设置由两个相同的传感器组成，通过功分器和等长电缆连接到同一根天线。传感器位于建筑物的屋顶上，如图4所示。

每个传感器由一个RTL-SDRv3 “Silver” 型号[4]连接至 Raspberry Pi-3[2]构成。自动增益控制增益被设置为一个固定值，并手动调节以最大化数据包解码率。采样率设置为f s = 2.4MHz，这是我们设备在不丢失样本的情况下能够达到的最高采样率。每个I/Q 样本以8位表示。完整的IQ样本流被录制一次，并多次离线处理。我们的结果基于2017年8月2日在图恩（瑞士）09:41采集的5分钟样本轨迹。使用dump1090 开源工具[1]在两个传感器上均正确解码的广播式自动相关监视报文数量为26445个，来自59架不同的飞机。

4.3 评估指标

在本节中，我们简要描述了用于评估不同到达时间估计方法精度所采用的方法。该问题并不简单，因为我们的接收机未同步且“真实”的到达时间未知。因此，我们开发了一种评估方法，能够在没有真实值的情况下量化到达时间的精度。

用 tm , i 表示数据包 m 到接收机 i 的 真实 绝对到达时间，用 ˆ tm , i 表示相应的 测量 到达时间（由待测方法）。通常，测量值 ˆtm,i 受到两种不同的误差源影响，即时钟误差和测量噪声：

ˆtm, i= tm, i+ ξ i(t)|t=tm, i + ϵm, i. (2)

术语ξ i(t)用于建模接收机时钟与绝对时间参考之间的时钟误差，并可通过一个随时间缓慢变化的函数进行建模。其大小取决于设备的硬件特性，特别是本地振荡器的稳定性。

术语ϵ m,i表示到达时间估计过程中的测量噪声，由一个零均值且方差为 σ2TOA的随机变量建模。到达时间估计的精度定义为噪声方差的倒数，与时钟误差无关。本研究的目标是降低 σ2TOA。抵消时钟误差分量的问题不在本文的研究范围内。

此处只需指出，可通过采用带有GPS驯服振荡器（GPSDO）的接收机来减轻时钟误差，或者在后处理中对其进行估计和补偿[7–9]。

接下来，我们将阐述一种实验方法，用于量化经验到达时间标准差ˆσTOA，即使存在非零的时钟误差分量。首先，我们需要消除式（2）中未知的真实绝对到达时间tm,i。由于我们使用两个连接到同一根天线的相同接收机，可以设tm,1= tm, 2 = tm，然后将两个传感器处的到达时间测量值相减，得到相应的时间差：

Δˆt m def = ˆt m,2 − ˆt m,1 = Δξ(tm)+ Δϵ m (3)

其中 Δξ(t) def = ξ 2( t) − ξ 1( t)表示复合时钟误差，Δϵ m def = ϵ m,2 − ϵ m,1为具有方差 σ 2 Δϵ = 2σ 2 到达时间的复合测量误差。在短时间尺度下，在过程 Δξ(t)的相干时间内，时钟误差表现为系统误差，即一种可估计并消除的bias项，以便

5 数值结果

我们现在展示在测试平台上评估的不同到达时间估计方法的精度结果。

5.1 误差分布

在图5中，我们绘制了测试轨迹中所有数据包使用不同到达时间估计方法得到的残差 Δϵ的经验累积分布函数（ECDF）。相应的到达时间误差标准差ˆσTOA的值列于表1的最左列。

对于计算负载较为关键的应用，有必要研究不同方法在升采样因子取中等值时的性能（N= 25）。对于CorrPacket和 CorrPulse，我们采用具有二进制0/1值的矩形脉冲形状，以实现较低计算负载。参考图5(a)，我们观察到提出的 PeakPulse算法达到了RMSEΔϵ= 3.15 ns，不到传统 CorrPacket/R方法的一半。值得注意的是，该优异结果是在没有进行互相关操作的情况下获得的。图6显示了不同升采样因子N下的ˆσTOA。我们观察到，随着N的增加，提出的方法 PeakPulse和CorrPulse/R的精度提升更快，优于 CorrPacket/R。这些结果表明，在计算负载至关重要的情况下，应优先选择PeakPulse方法。

接下来，我们考虑那些拥有充足计算能力的应用场景，其主要目标是最大化精度，而无需担心计算负载。对于这些应用场景，可以方便地采用更高的上采样因子（在本例中为N= 83），并且对于互相关方法，可使用更为复杂的“平滑”脉冲形状。后者更接近于通过RTL-SDR前端传输后的实际脉冲形状，因此相比简单的“矩形”形状能带来稍高的精度，这一点可以从表1中得到验证。这些方法的残差Δϵ的经验累积分布函数（ ECDF）如图5(b)所示。可以看出，所提出的CorrPulse/S方法比经典的CorrPacket/S方法具有更高的精度，并实现了RMSE Δϵ = 2.16 ns，对应ˆσTOA = 1.51 ns。

5.2 误差与信号强度

接下来，我们研究信号强度对使用最精确方法（即CorrPulse/S N= 83）获得的到达时间误差的影响。对于任意数据包m和传感器i，我们用γ m,i表示所有脉冲的脉冲高度平方的平均值——作为到达数据包强度的指标。此外，我们用β m,i表示在接收机中因一个或多个对应的IQ样本使ADC饱和而导致削波的脉冲数量。

在图7中，我们针对每个单独的数据包m绘制了使用 CorrPulse/S(N= 83) 获得的残差误差绝对值 |Δϵ m| 与两个传感器之间的平均信号强度γ m def = (γ m,1 + γ m,2)/2 的关系。每个数据包被分为三个类别之一：当 γ m ≤ 0.04 时标记为“L”类；当 mini=1,2 β m,i ≥ 10 时标记为“H”类；其余所有数据包标记为“M”类。这三个类别在图7中分别用黑色、红色和蓝色标记表示。各类别下每种方法得到的估计的到达时间误差标准差列于表1中。一端，“L”类低强度数据包的定时估计受到量化噪声的影响；另一端，高强度接收的数据包则受到模数转换器削波这种失真的影响，明显降低了定时精度。正如预期，这两类在所有方法下均产生较大的误差。介于两者之间的是“M”类数据包，其信号强度很好地匹配了动态范围：对于此类数据包，提出的方法实现了 ˆσTOA = 0.79 ns 的到达时间精度。

在我们的迹线中，少于60%的所有数据包属于“M”类。通过使用更优硬件，特别是增加模数转换器位数和更大的动态范围，可以调整自动增益控制增益，从而提高落入该类别的数据包比例，进而提升整体精度。

上述结果表明，接收分组度量γ m,1 和 β m,i 可用于为每一次到达时间测量TOA measurement ˆtm,i 提供预期精度的指示，影响每个单独测量的误差方差ˆσ²m,i。通过这种方式，以到达时间测量为输入（例如用于位置估计）的算法可以最优地加权每个单独的输入测量值，如加权最小二乘法[23]中所采用的方法。

最后，我们发现在每一类中，经验误差分布与高斯分布非常接近，如图8中的正态Q-Q图所示。这证明了基于输入的到达时间测量[7], 进行位置估计问题时采用最小二乘法（LS）是合理的，因为当输入误差服从正态分布时，最小二乘法解与最大似然估计一致。

估计方法	ˆσTOA[纳秒] 所有数据包	ˆσTOA[纳秒] L	ˆσTOA[纳秒] M	ˆσTOA[纳秒] H
传统的 dump1090	45.20	44.94	45.19	45.43
SenSys’17，N= 25	5.90	6.11	5.88	5.78
CorrPacket/R, N= 25	4.98	5.48	4.85	4.94
CorrPacket/R, N= 83	2.14	3.04	1.78	2.35
CorrPacket/S, N= 83	2.07	3.00	1.68	2.275
CorrPulse/R, N= 25	1.89	2.75	1.56	1.86
CorrPulse/R, N= 83	1.63	2.72	1.04	1.77
CorrPulse/S, N= 83	1.51	2.60	0.79	1.77
PeakPulse, N= 25	2.20	3.36	1.70	2.23
PeakPulse, N= 83	2.12	3.44	1.62	2.17

表1：到达时间误差标准差的经验估计 ˆσTOA。

6 结论与展望

我们提出了两种新型S模式信号到达时间估计方法的变体，这两种方法不依赖于与完整数据包模板进行长时间互相关。其中精度最高的变体，即CorrPulse/S，仅对单个脉冲执行短时互相关操作。另一种变体，即PeakPulse，计算更轻量，无需任何互相关操作，且在中等升采样因子下也能良好工作。我们已经证明，此类算法即使使用当前最廉价的SDR硬件（即RTL-SDR）捕获的实际信号，也能实现纳秒级精度的到达时间估计。进一步分析测试结果表明，使用RTL-SDR时影响到达时间估计精度的主要限制因素是有限动态范围——由于8位模数转换器和固定自动增益控制导致动态范围小于50 dB，从而导致大量数据包发生削波或淹没于量化噪声中。对于接收信号强度处于接收机动态范围内的情况，CorrPulse/S可实现亚纳秒精度。可以预期，使用更优硬件能够进一步提高精度。

PeakPulse方法已用C语言实现，集成于dump1090接收机中，并以开源形式发布¹。

¹ http://github.com/openskynetwork/dump1090‐hptoa