数组归纳
1. 滑动窗口
- 关键字:"子串"、"连续"、"子xxx(如子数组)"
- 例子:
209. 长度最小的连续子数组、76.最小覆盖子串 - 套路:维护一个左指针l、右指针r,通过不断扩张和收缩来满足题目约束
-
- 左指针扩张:右指针
r++往右走,把元素纳入窗口 - 右指针收缩:如果窗口内条件不满足(如和太大/字符不满足),移动左指针
l++缩小窗口
- 左指针扩张:右指针
2. 双指针
- 例子:
283. 移动零、11. 盛最多水的容器 - 套路:
-
- 快慢指针:右指针扫描,判断条件并交换或记录
- 双指针夹逼:左右两端向中间收缩,更新或记录条件
3. 前缀和
- 定义:前缀和数组
s,其中
-
s[0] = 0(类似哨兵节点)s[i] = nums[0] + nums[1] + ... + nums[i-1]
- 用途:任意区间
[l, r]的和 =s[r+1] - s[l]
-
- 相当于把"求区间和"的问题转化为"两个前缀和相减"
- 例子:
53. 最大子数组和、238. 除自身以外数组的乘积
4. 区间问题
- 概念: 是一类需要处理区间区间关系的题目,本质上是处理多个
[l、r]的关系 - 套路:一般用排序做预处理,因为区间没有顺序时不好比较,排好序后才能高效遍历、合并
- 例子:
56. 合并区间
5. 数组操作
- 定义:将数组算法题中一些不具通用性的思想归为该类,主要记住方法即可
-
189. 轮转数组:学会数组拷贝函数41. 缺失的第一个正数:原地哈希
209.长度最小的连续子数组
题目:

解答:滑动窗口
思路:滑动窗口,满足时r扩张,不满足时l收缩
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int left = 0;
int sum = 0;
int result = Integer.MAX_VALUE; // 记录当前最小长度
// # 模板:右指针扩张
for (int right = 0; right < nums.length; right++) {
sum += nums[right];
// # 模板:左指针收缩,如果总和大于target(满足条件)
while (sum >= target) {
result = Math.min(result, right - left + 1);
sum -= nums[left++];
}
}
return result == Integer.MAX_VALUE ? 0 : result;
}
}
76.最小覆盖子串
题目:

学习:int[]代替Set、substring()左闭右开
- 可以用数组代替哈希表的功能,如题有char(含大小写)的情况,直接用
int[128]配合isCover()判断是否覆盖 String.substring()是左闭右开
解答:滑动窗口
思路:滑动窗口,用cntS、cntT记录字母出现次数,如果覆盖其子串更短,则记录
class Solution {
public String minWindow(String S, String t) {
int[] cntS = new int[128]; // s 子串字母的出现次数
int[] cntT = new int[128]; // t 中字母的出现次数
for (char c : t.toCharArray()) {
cntT[c]++;
}
char[] s = S.toCharArray();
int m = s.length;
int ansLeft = -1; // 记录要返回的l(初始化为不可能值,用于判断是否返回失败)
int ansRight = m; // 记录要返回的r
int left = 0;
for (int right = 0; right < m; right++) { // #模板:扩展右指针
cntS[s[right]]++;
// 判断是否覆盖
while (isCovered(cntS, cntT)) {
// 如果找到更短的子串,记录此时的左右端点
if (right - left < ansRight - ansLeft) {
ansLeft = left;
ansRight = right;
}
// # 模板:收缩左指针(同时收缩记录)
cntS[s[left]]--;
left++;
}
}
return ansLeft < 0 ? "" : S.substring(ansLeft, ansRight + 1);
}
private boolean isCovered(int[] cntS, int[] cntT) {
for (int i = 'A'; i <= 'Z'; i++) {
if (cntS[i] < cntT[i]) {
return false;
}
}
for (int i = 'a'; i <= 'z'; i++) {
if (cntS[i] < cntT[i]) {
return false;
}
}
return true;
}
}
283.移动零:
题目:

解答:双指针-快慢指针
思路(记方法):双指针,右指针找到最近的非零元素,与左边界交换;左指针维护一个左边界(所有零在这个边界上或它右边),每次交换一个非零元素到左边界,左边界右移
class Solution {
public void moveZeroes(int[] nums) {
int n = nums.length, left = 0, right = 0;
// # 模板:右指针扫描
while (right < n) {
if (nums[right] != 0) {
swap(nums, left, right);
left++;
}
right++;
}
}
public void swap(int[] nums, int left, int right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
}
11.盛最多水的容器
题目:

解答:双指针-双指针夹逼
思路:两指针在左右边界,每次较短一根向中间移动,并更新最大容量
- 为什么两个指针初始化在两边:因为这是最左和最右,而最优情况一定是这两指针之间的两个柱子
- 为什么每次移动较短的那根:移动哪一根都是减少1宽度,那么移动短的一根得到的结果显然更大
public class Solution {
public int maxArea(int[] height) {
int l = 0, r = height.length - 1;
int ans = 0;
while (l < r) {
int area = Math.min(height[l], height[r]) * (r - l);
ans = Math.max(ans, area);
if (height[l] <= height[r]) {
++l;
}
else {
--r;
}
}
return ans;
}
}
53.最大子数组和
题目:

解答:前缀和
思路:计算最大子数组和,只需要计算该数组的终点前缀和-起点前缀和,而起点前缀和越小越好。所以遍历数组,维护一个当前最小前缀和,遍历到的元素求前缀和并当作终点前缀和进行计算
class Solution {
public int maxSubArray(int[] nums) {
int ans = Integer.MIN_VALUE;
int minPreSum = 0;
int preSum = 0;
for (int x : nums) {
preSum += x; // 当前的前缀和:上一位前缀和 + x
ans = Math.max(ans, preSum - minPreSum); // 当前子数组是否更大
minPreSum = Math.min(minPreSum, preSum); // 维护最小前缀和
}
return ans;
}
}
238.除自身以外数组的乘积
题目:
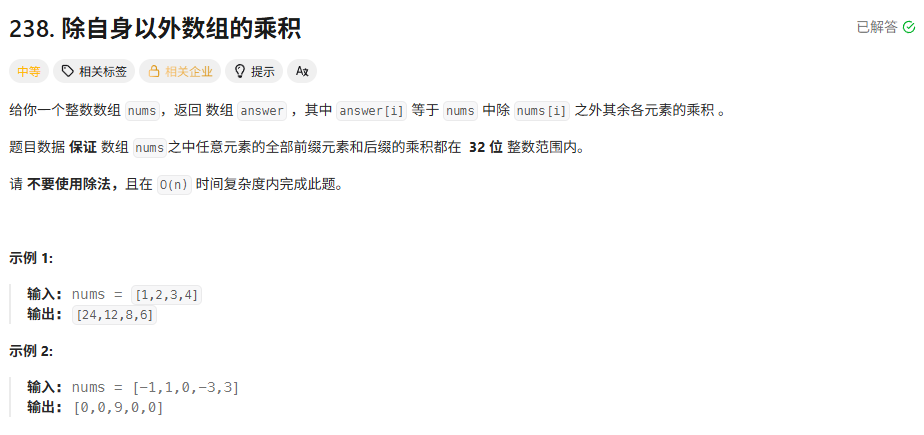
解答:"前缀和"思想
思路(记方法):answer = 左边的总乘积 * 右边的总乘积,那么维护前缀和(前缀积)数组和后缀和数组,相乘即得到答案
class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] anwser = new int[n];
int[] pre = new int[n]; // 前缀积
pre[0] = 1;
int[] suf = new int[n]; // 后缀积
suf[n - 1] = 1;
for (int i = 1; i < n; i++) {
pre[i] = pre[i - 1] * nums[i - 1];
}
for(int i = n - 2; i >= 0; i--) {
suf[i] = suf[i + 1] * nums[i + 1];
}
for (int i = 0; i < n; i++) {
anwser[i] = pre[i] * suf[i];
}
return anwser;
}
}
56.合并区间
题目:

解答:区间问题
思路:
- 先将
intervals按左端点排序(方便后续遍历与合并) - 先将第一个区间作为待合并区间,遍历数组,比较当前区间的左端点是否在合并区间之间,判断是否合并
-
- 合并:更新待合并区间的右端点
- 不合并:不符合条件,收集结果并将下一区间作为待合并区间
如下,把ans最后一个元素当作待合并区间
class Solution {
public int[][] merge(int[][] intervals) {
Arrays.sort(intervals, (p, q) -> p[0] - q[0]); // 左端点从小到大排序
List<int[]> ans = new ArrayList<>();
for (int[] p : intervals) {
int m = ans.size();
// 如果可以合并,则判断并更新待合并区间的右端点
if (m > 0 && p[0] <= ans.get(m - 1)[1]) {
ans.get(m - 1)[1] = Math.max(ans.get(m - 1)[1], p[1]);
} else { // 不相交,无法合并,则收集结果
ans.add(p);
}
}
return ans.toArray(new int[ans.size()][]);
}
}
189.轮转数组
题目:

学习:数组拷贝函数System.arraycopy()
System.arraycopy(nums, l2, ans, 0, n - l2);
nums:源数组l2:源数组的起始复制位置(即从nums[l2]开始复制)ans:目标数组0:目标数组的起始粘贴位置(即粘贴到ans[0]开始)n - l2:要复制的元素个数
解答:数组操作-加k取余实现轮转
思路(记方法):只需要抓住规律即可,配合取余进行赋值,用数组拷贝拷贝回原数组
class Solution {
public void rotate(int[] nums, int k) {
int n = nums.length;
int[] newArr = new int[n];
for (int i = 0; i < n; ++i) {
// +k表示轮转次数,取余表示超界时返回起点再轮转
newArr[(i + k) % n] = nums[i];
}
System.arraycopy(newArr, 0, nums, 0, n);
}
}
41.缺失的第一个正数
题目:

解答:数组操作-原地哈希
技巧:如果没有限制空间,可以放进哈希表并遍历得到最小正数;但是限制了空间,可以采用"原地哈希"来节省空间
思考:数组长度为n,则"最小正数"最小值为n+1,即整个数组为1 -> n
思路:遍历nums数组,如果当前nums[x]符合1 ≤ x ≤ n,而且nums[x]对应位置nums[nums[x] - 1]还没有放过,则交换x和nums[x] - 1下标元素;但是,交换之后,x位置的新值也可能需要交换去别的地方,所以需要while循环,直到x位置的值不符合交换条件,才算解决了x位置,才能继续往后递归
class Solution {
public int firstMissingPositive(int[] nums) {
int n = nums.length;
// 1.将每个数 x 放到下标 x-1 的位置
for (int i = 0; i < n; i++) {
// 只放范围在(1 ≤ x ≤ n)的x,超范围的不用管
// 已经放过的不用重复放,避免循环
while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
int tmp = nums[nums[i] - 1];
nums[nums[i] - 1] = nums[i];
nums[i] = tmp;
}
}
// 2.如果nums[i] != i+1,说明 i+1 就是缺失的最小正整数
for (int i = 0; i < n; i++) {
if (nums[i] != i + 1) {
return i + 1;
}
}
// 3.如果都在正确位置,返回 n+1
return n + 1;
}
}




















 869
869

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








