速通回溯算法：套路总结+实战练习

回溯算法归纳

框架：

几乎所有回溯题都遵循同一个框架：

void dfs(参数...) {
    if (递归出口) {
        收集结果;
        return;
    }

    for (选择 : 可选的选项们) {
        做选择;      // 加入路径
        dfs(...);   // 递归下一层
        撤销选择;    // 回溯
    }
}

三个关键步骤：

1. 做选择：把一个元素加到“路径”里
2. 递归：进入下一层，继续处理后续问题
3. 撤销选择：恢复现场，把这个元素拿掉，回到上一步

可以把回溯看作“试错 + 回退”：先大胆尝试，如果走不通就退回上一步，换一条路继续

分类：

我们可以把常见回溯问题分成几类：

1. 排列类（可回退）

• • 例子：46. 全排列
  • 特点：路径的元素可以重新选择前面排除过的（只要没用过就行），所以不需要维护start下标
  • 用 visited 或 onPath 数组来记录哪些元素已经用过

1. 子集类/组合类（不回退）

• • 例子：78. 子集、39. 组合总和
  • 特点：路径的元素只能往后选，不能回退去选前面已经排除的，所以需要维护start下标

1. 构造类（有效性约束生成）

• • 例子：22. 括号生成
  • 特点：不需要遍历候选集合，从空状态逐步构造一个满足约束的解，每一步的选择有合法性条件，不合法就不递归

1. 切割类（分割字符串）

• • 例子：131. 分割回文串
  • 特点：路径是分割点，不能回退到前面，需要维护start

1. 棋盘搜索类（二维DFS）

• • 例子：79. 单词搜索
  • 特点：需要标记走过的位置，注意这里的模板顺序会有差别

剪枝：即检查当前是否合法，如果不合法则提前退出遍历，是一种优化手段

---

46.全排列

题目：

解答：排序类回溯

排列类回溯：允许重新选择之前排除过的，不需要维护start下标，只需要维护visited数组

思路：遍历数组，如果元素不在路径path中，则添加进路径，递归后进行回溯移除该元素

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();
        List<Integer> path = Arrays.asList(new Integer[nums.length]);
        boolean[] onPath = new boolean[nums.length];
        
        dfs(0, nums, ans, path, onPath);
        return ans;
    }

    private void dfs(int i, int[] nums, List<List<Integer>> ans, List<Integer> path, boolean[] onPath) {
        // # 模板：定义递归出口
        if (i == nums.length) {
            ans.add(new ArrayList<>(path)); // 注意，这里需要拷贝（⭐）
            return;
        }
        
        for (int j = 0; j < nums.length; j++) { // # 模板：遍历
            if (!onPath[j]) { 
                // # 模板；做选择（将元素加入路径）
                path.set(i, nums[j]);
                onPath[j] = true;

                // # 模板：递归下一层
                dfs(i + 1, nums, ans, path, onPath); 

                // # 模板：回溯（恢复现场）
                onPath[j] = false;
                // path 无需回溯：因为遍历递归中，path第i个元素会被直接覆盖
            }
        }
    }
}

---

78.子集

题目：

解答：子集类回溯

子集类回溯：不允许重新选择前面排除过的，需要维护start下标（用于递归中传递当前位置）

思路：维护start下标用于递归，每次递归都收集结果；path长度不定所以用List维护

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();
        dfs(nums, 0, new ArrayList<>(), ans);
        return ans;
    }

    private void dfs(int[] nums, int start, List<Integer> path, List<List<Integer>> ans) {
        // # 模板：递归出口（收集结果，这里每次递归都收集）
        ans.add(new ArrayList<>(path));

        // # 模板：遍历
        for (int i = start; i < nums.length; i++) {
            // # 模板：做选择
            path.add(nums[i]);

            // # 模板：递归
            dfs(nums, i + 1, path, ans);

            // # 模板：回溯，按下标移除最后一个元素
            path.remove(path.size() - 1);
        }
    }
}

---

39.组合总和

题目：

解答：子集类回溯

子集类/组合类回溯：不允许重复选择之前已选的元素，维护start下标用于递归

组合类相比子集类，多了一个"和为target"的条件，需要配合剪枝进行优化（不符合条件后，跳过本轮递归）

思路：维护一个remain变量记录距离target还剩多少，配合剪枝进行优化

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates); // 排序便于剪枝
        List<List<Integer>> ans = new ArrayList<>();
        
        dfs(candidates, 0, target, new ArrayList<>(), ans);
        return ans;
    }

    private void dfs(int[] candidates, int start, int remain, List<Integer> path, List<List<Integer>> ans) {
        // # 模板：定义递归出口，收集结果
        if (remain == 0) {
            ans.add(new ArrayList<>(path));
            return;
        }

        // # 模板：遍历
        for (int i = start; i < candidates.length; i++) {
            // # 模板：做选择，
            int val = candidates[i];
            if (val > remain) break; // 剪枝：因为candidates是顺序的，所以往后都不用遍历了
            path.add(val);

            // # 模板：递归
            dfs(candidates, i, remain - val, path, ans); // 传 i 允许重复使用

            // # 模板：回溯
            path.remove(path.size() - 1);
        }
    }
}

---

22.括号生成

题目：

解答：构造类回溯

构造类回溯：不需要遍历数组，逐步构建符合条件的结果，每一步都需要判断是否符合条件

学习：这一类回溯，一般都是根据条件维护一些变量等，在每次递归时判断是否合法

思路：维护left、right变量表示左、右括号的数量。当左括号小于n，则可以放左括号；当右括号小于左括号，则可以放右括号（可以记一下）

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> ans = new ArrayList<>();
        
        dfs(new StringBuilder(), 0, 0, n, ans);
        return ans;
    }

    private void dfs(StringBuilder path, int left, int right, int n, List<String> ans) {
        // # 模板：定义递归出口，收集结果
        if (path.length() == 2 * n) {
            ans.add(path.toString());
            return;
        }

        // # 模板：（根据条件是否合法）做选择
        if (left < n) { // 可以放左括号
            path.append('(');

            // # 模板：递归
            dfs(path, left + 1, right, n, ans);

            // # 模板：回溯
            path.deleteCharAt(path.length() - 1);
        }
        
        if (right < left) { // 可以放右括号
            path.append(')');

            // # 模板：递归
            dfs(path, left, right + 1, n, ans);

            // # 模板：回溯
            path.deleteCharAt(path.length() - 1);
        }
    }
}

---

79.单词搜索

题目：

解答：棋盘搜索类

棋盘搜索类：在二维数组上操作，需要标记已访问的元素

思路：把二维数组每个元素当作递归起点，判断当前元素是否合法，并向四个方向递归，最后返回结果

class Solution {
    public boolean exist(char[][] board, String word) {
        int m = board.length, n = board[0].length;
        char[] w = word.toCharArray();

        // 遍历整个二维数组，每一个都当作起点
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (dfs(board, w, 0, i, j)) {
                    return true;
                }
            }
        }
        return false;
    }

    private boolean dfs(char[][] board, char[] w, int idx, int r, int c) {
        // # 模板：过滤失败条件
        if (r < 0 || r >= board.length || c < 0 || c >= board[0].length) {
            return false;
        }
        if (board[r][c] != w[idx]) {
            return false;
        }

        // # 模板：定义递归出口（word最后一个字母，结束递归）
        if (idx == w.length - 1) {
            return true;
        }

        // # 模板：做选择，选择当前元素（因为符合条件）
        char saved = board[r][c];
        board[r][c] = '\0'; 

        // # 模板：遍历（四个方向的递归可以看成遍历）
        // # 模板：递归
        boolean found = dfs(board, w, idx + 1, r + 1, c)
                || dfs(board, w, idx + 1, r - 1, c)
                || dfs(board, w, idx + 1, r, c + 1)
                || dfs(board, w, idx + 1, r, c - 1);

        // # 模板：回溯（将保存的saved设置回去）
        board[r][c] = saved;

        // # 模板：定义递归出口
        return found;
    }
}

---

131.分割回文串

题目：

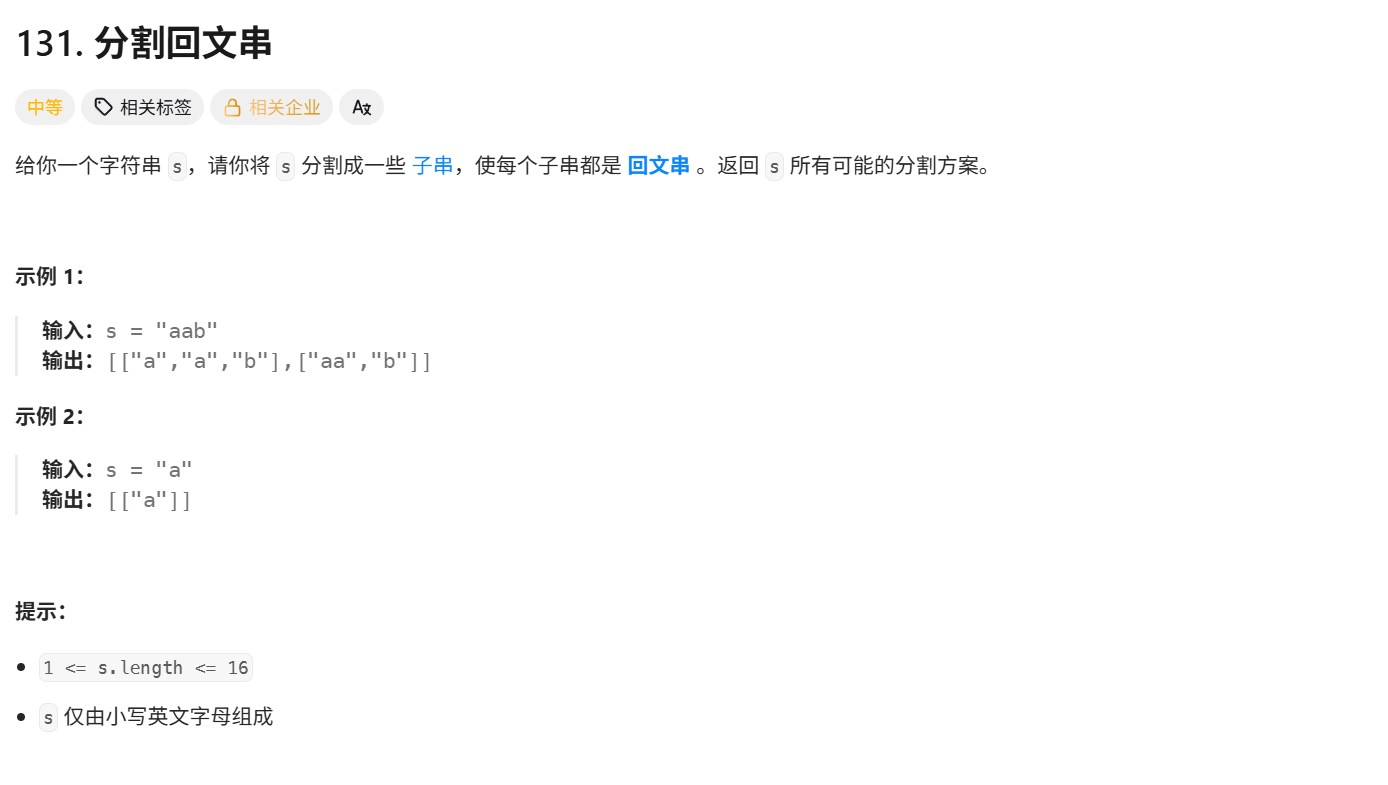
解答：切割类回溯

切割类回溯：路径是分割点，不能回退到前面，需要维护start

思路：维护start下标，如果当前是回文串则切，然后递归；如果不是回文串则剪枝（if判断直接continue也行），直接遍历下一个元素

class Solution {
    public List<List<String>> partition(String s) {
        List<List<String>> ans = new ArrayList<>();
        
        dfs(s, 0, new ArrayList<>(), ans);
        return ans;
    }

    private void dfs(String s, int start, List<String> path, List<List<String>> ans) {
        // # 模板：递归出口，收集结果
        if (start == s.length()) {
            ans.add(new ArrayList<>(path));
            return;
        }

        // # 模板：遍历
        for (int end = start; end < s.length(); end++) {
            // # 模板：剪枝，必须是回文串才能继续
            if (!isPalindrome(s, start, end)) continue;

            // # 模板：做选择，加入当前子串
            path.add(s.substring(start, end + 1));

            // # 模板：递归
            dfs(s, end + 1, path, ans);

            // # 模板：回溯
            path.remove(path.size() - 1);
        }
    }

    // 辅助方法：判断 s[l..r] 是否是回文
    private boolean isPalindrome(String s, int l, int r) {
        while (l < r) {
            if (s.charAt(l++) != s.charAt(r--)) return false;
        }
        return true;
    }
}