《李宏毅机器学习》task2
1.偏差和方差
学习误差由偏差和方差而产生
-
偏差与方差分别是用于衡量一个模型泛化误差的两个方面;
模型的偏差,指的是模型预测的期望值与真实值之间的差;
模型的方差,指的是模型预测的期望值与预测值之间的差平方和; -
偏差用于描述模型的拟合能力;
方差用于描述模型的稳定性。
记在训练集 D 上学得的模型为
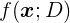
模型的期望预测为
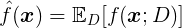
偏差(Bias)
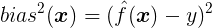
方差(Variance)
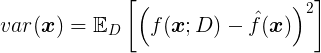
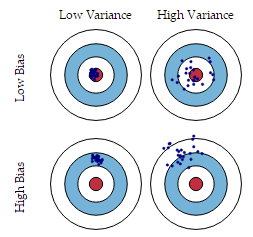
bias描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距,简单讲,就是在样本上拟合的好不好。要想在bias上表现好,low bias,就得复杂化模型,增加模型的参数,但这样容易过拟合 (overfitting),过拟合对应上图是high variance,点很分散。low bias对应就是点都打在靶心附近,所以瞄的是准的,但手不一定稳。
varience描述的是样本上训练出来的模型在测试集上的表现,要想在variance上表现好,low varience,就要简化模型,减少模型的参数,但这样容易欠拟合(unfitting),欠拟合对应上图是high bias,点偏离中心。low variance对应就是点都打的很集中,但不一定是靶心附近,手很稳,但是瞄的不准。
在机器学习中,一般将样本分成独立的三部分训练集(train set),验证集(validation set)和测试集(test set)。其中,测试集用来检验最终选择最优的模型的性能如何。
过拟合,欠拟合
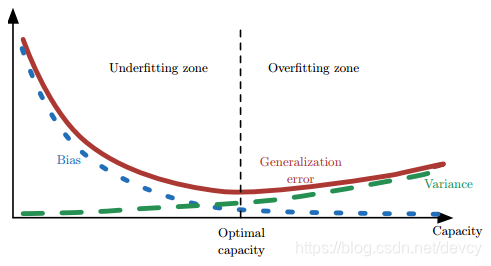
当训练不足时,模型的拟合能力不够(数据的扰动不足以使模型产生显著的变化),此时偏差主导模型的泛化误差;
随着训练的进行,模型的拟合能力增强(模型能够学习数据发生的扰动),此时方差逐渐主导模型的泛化误差;
当训练充足后,模型的拟合能力过强(数据的轻微扰动都会导致模型产生显著的变化),此时即发生过拟合(训练数据自身的、非全局的特征也被模型学习了)
2.鞍点,全局最优和局部最优
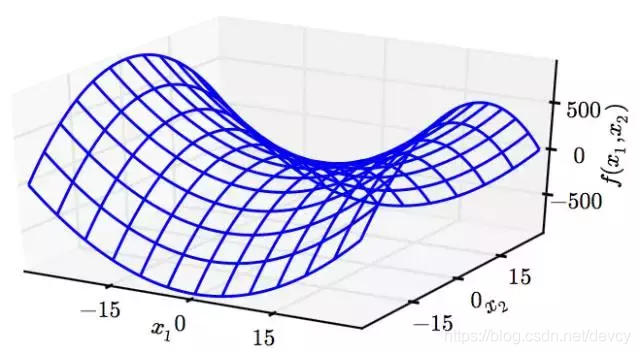
3.梯度下降
Mini-Batch与SGD
全量梯度下降法(Batch gradient descent)
全量梯度下降法每次学习都使用整个训练集,因此每次更新都会朝着正确的方向进行,最后能够保证收敛于极值点,凸函数收敛于全局极值点,非凸函数可能会收敛于局部极值点,缺陷就是学习时间太长,消耗大量内存。
SGD一轮迭代只用一条随机选取的数据,尽管SGD的迭代次数比BGD大很多,但一次学习时间非常快。
SGD的缺点在于每次更新可能并不会按照正确的方向进行,参数更新具有高方差,从而导致损失函数剧烈波动。不过,如果目标函数有盆地区域,SGD会使优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点,这样对于非凸函数,可能最终收敛于一个较好的局部极值点,甚至全局极值点。
缺点是,出现损失函数波动,如下图所示,并且无法判断是否收敛
SGD相比BGD收敛速度快,然而,它也的缺点,那就是收敛时浮动,不稳定,在最优解附近波动,难以判断是否已经收敛。这时折中的算法小批量梯度下降法,MBGD就产生了,道理很简单,SGD太极端,一次一条,为何不多几条?MBGD就是用一次迭代多条数据的方法。
并且如果Batch Size选择合理,不仅收敛速度比SGD更快、更稳定,而且在最优解附近的跳动也不会很大,甚至得到比Batch Gradient Descent 更好的解。这样就综合了SGD和Batch Gradient Descent 的优点,同时弱化了缺点。总之,Mini-Batch比SGD和Batch Gradient Descent都好。
Batch与Mini-Batch,SGD的区别
如何根据样本大小选择哪个梯度下降
写出SGD和Mini-Batch的代码
4.交叉验证
5.归一化
6.回归模型评价指标
SSE(误差平方和):The sum of squares due to error
R-square(决定系数):Coefficient of determination
Adjusted R-square:Degree-of-freedom adjusted coefficient of determination





 博客围绕机器学习展开,介绍学习误差由偏差和方差产生,阐述过拟合、欠拟合情况。讲解鞍点、全局最优和局部最优,重点分析梯度下降,对比全量、SGD、Mini - Batch方法,还提及交叉验证、归一化和回归模型评价指标。
博客围绕机器学习展开,介绍学习误差由偏差和方差产生,阐述过拟合、欠拟合情况。讲解鞍点、全局最优和局部最优,重点分析梯度下降,对比全量、SGD、Mini - Batch方法,还提及交叉验证、归一化和回归模型评价指标。
















 417
417

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








