李宏毅机器学习-task2

• 理解偏差和方差

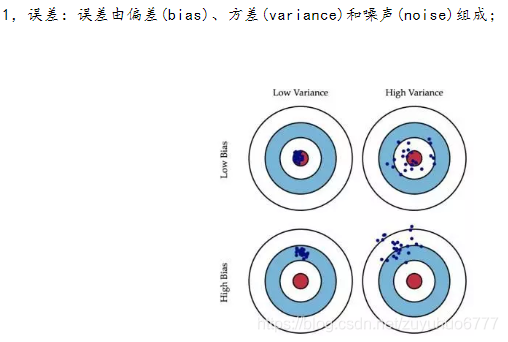
1.1，偏差：

  偏差度量了学习算法的期望预测与真实结果的偏离程度，刻画了学习算法本身的拟合能力。也即，偏差（Bias）描述了预测值（估计值）的期望与真实值之间的差距，偏差越大，越偏离真实数据。偏差可看做是“有监督的”，有人的知识参与的一个指标。即：高偏差是欠拟合

1.2，方差：

  方差度量了同样大小的训练集的变动所导致的学习性能的变化，刻画了数据扰动所造成的影响。也即，方差（Variance）描述的是预测值的变化范围，离散程度，也就是离其期望值的距离，方差越大，数据的分布越分散。

即高方差是过拟合。方差可看做是“无监督的”，客观的指标。

1.3，噪声：

  噪声表达了当前任务上任何学习算法所能达到的期望泛化误差的下界，刻画了学习问题本身的难度。

 

 

 

• 学习误差为什么是偏差和方差而产生的，并且推导数学公式

•  

• 过拟合，欠拟合，分别对应bias和variance什么情况

过拟合：bias很小，而variance很大，说明模型过于复杂，把训练样本的自身的非全局特征都学过去了。
欠拟合：bias很大。模型太简单，对训练样本的一般性质没有学到位。

 

• 学习鞍点，复习上次任务学习的全局最优和局部最优

定义：

目标函数在此点上的梯度为0，但从该点出发的一个方向是函数的极大值点，而在另一个点方向是函数的极小值点。

 

 

• 解决办法有哪些

•  

• 梯度下降

 

 

 

 

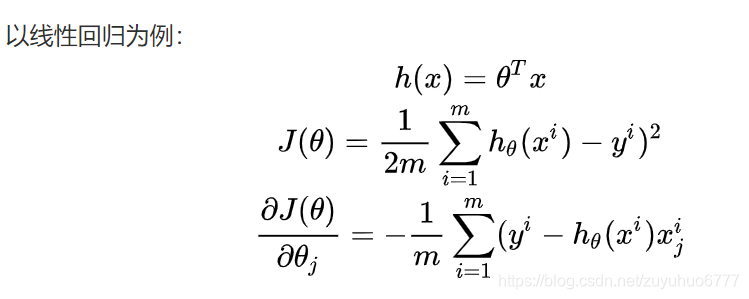
• 学习Mini-Batch与SGD

• 学习Batch与Mini-Batch，SGD梯度下降的区别

• 如何根据样本大小选择哪个梯度下降(批量梯度下降，Mini-Batch）

• 写出SGD和Mini-Batch的代码

• 学习交叉验证

先将数据集D划分成k个大小相似的互斥子集：
每个子集的分布尽量保持一致
训练时，每次使用个子集作为训练集，1个子集作为测试集，这样就有种选择，进行次训练和测试，返回个结果的均值。
一般也称为k折交叉验证法，可以取5,10,20等。
子集的划分可能存在多种方式，为了减小因样本划分不同而引入的差别，折交叉验证通常需要随机使用不同的划分重复次，并取均值，这叫做次折交叉验证。
越大，模型的实际训练效果与样本数据集的期望预测结果越相似，特别的，当等于中全部样本个数时，意味着只保留一个样本作为训练集，也被称为留一法。
留一法的评估结果比较准确，但是在样本较大时很费时间。

 

• 学习归一化

归一化之后，等高线比较“圆”，寻优过程更加平缓，更容易收敛。
归一化的公式：
标准化公式：
归一化和标准化的本质都是线性变换，先压缩，后平移，线性变换不会改变数值的排序，反而还能提高数据的表现。

• 学习回归模型评价指标