一句话理解可导与连续的关系

有一条经典的语句 “可导一定连续，但连续不一定可导”。看起来前半句好理解，但后半句很难让人理解。不妨来个反例，一讲就明白了。
要获得更多有趣而又通俗的微积分知识，请学习《人人可懂的微积分——用动态、微观、累加的观点来看待微积分》，清华大学出版社出版。

函数$|x|$的图形如图 1 所示，看起来明显是连续的，在 “$x=0$” 时，函数图形有突变。这时，${\lim }_{x\to 0}|x|$的值是存在的，因为无论从左看还是从右看，函数的极限值都是 0，因此${\lim }_{x\to 0}|x|=0$。

但是此时，${\lim }_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$却不存在。因为从左边看，函数实际上是 “-x”，斜率是 - 1；从右边看，函数实际上是 “x”，斜率是 1，那导数值到底是多少？导函数选谁？相互之间产生了矛盾，此时也就意味着函数$|x|$不可导。

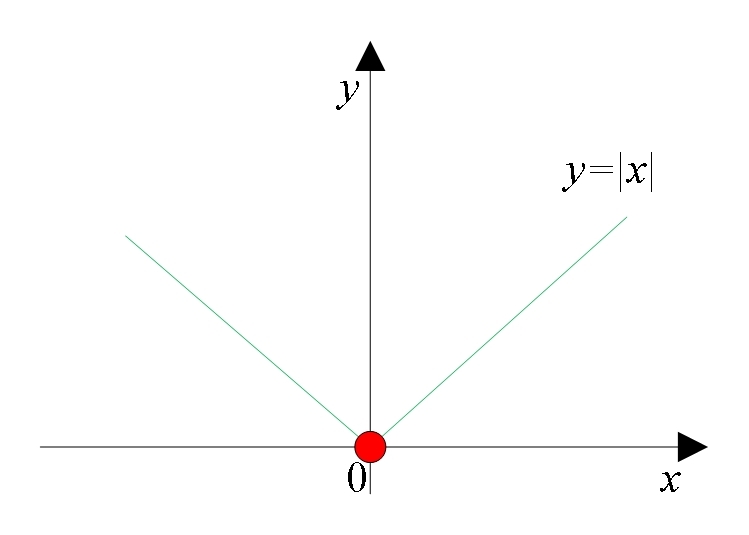
图 1 一个连续但不可导的函数示例
要获得更多有趣而又通俗的微积分知识，请学习《人人可懂的微积分——用动态、微观、累加的观点来看待微积分》，清华大学出版社出版。