Chapter3 Markov Decision Processes(MDP)

参考了《Reinforcement Learning: An Introduction》和
David Silver强化学习公开课，
这一章主要来自David Silver的ppt，建议直接看ppt，我只把容易犯错的地方点出来了

---

马尔科夫过程是强化学习的基础

---

Finite Markov Decision Processes

Markov property

A state $S_t$ is Markov if and only of

$$\mathbb{P}[S_{t+1}|S_t]=\mathbb{P}[S_{t+1}|S_1,\cdots,S_t]$$

• The state captures all relevant information from the history
• Once the state is know, the history may be thrown away
• i.e. The state is a sufficient statistic of the future

A Markov process is a memoryless random process, i.e. a sequence of random states $S_1,S_2,\cdots$ with the Markov property.
Markov Process

A Markov Process (or Markov Chain) is a tuple $\langle S,P \rangle$

• S is a (finite) set of states
• P is a state transition probability matrix, $P_{ss^\prime}=\mathbb{P}[S_{t+1}=s^\prime|S_t=s]$

A Markov reward process is a Markov chain with values.
Markov Reward Process

A Markov Process (or Markov Chain) is a tuple $\langle S,P,\color{red}{R,\gamma} \rangle$

• S is a (finite) set of states
• P is a state transition probability matrix, $P_{ss^\prime}=\mathbb{P}[S_{t+1}=s^\prime|S_t=s]$
• $\color{red}{\text{R is a reward function, $R_s=E[R_{t+1}|S_t=s]$}}$
• $\color{red}{\gamma \text{ is a discount factor, }\gamma \in [0,1]}$

注意这里$P_{ss^\prime}$的定义，是指从状态$s$到$s^\prime$的概率

后面常因为名字(return)忘记这个的定义，跟上面的单个Reward不一样
Return

The return $G_t$ is the total discounted reward from time-step t.

$$G_t=R_{t+1}+\gamma R_{t+2}+\cdots=\sum_{k=0}^{\infty} \gamma^k R_{t+k+1}$$

• The discount $\gamma \in [0,1]$ is the present value of future rewards
• The value of receiving reward R after k+1 time-steps is $\gamma^k R$
  
  • $\gamma$ close to 0 leads to “myopic(近视)” evaluation
  • $\gamma$ close to 1 leads to “far-sighted(远见)” evaluation
    后面提到的很多方法都是看的很远(远见)的

Value Function

The state value function v(s) of an $\color{red}{\text{MRP}}$ is the expected return starting form state s

$$v(s)=\mathbb{E}[G_t|S_t=s]$$

确实有必要看一下MRP的Bellman Equation，并与MDP对比。在MRP中没有考虑任何关于action的事情。因为MDP才是强化学习的主角，所以不看David Silver的ppt中的MRP实例了，容易对后面MDP的理解造成误解。
简单看一下Bellman Equation

$$\begin{align*} v(s) & = \mathbb{E} [G_t|S_t=s] \\ & = \mathbb{E} [R_{t+1}+\gamma v(S_{t+1})|S_t=s] \end{align*}$$
MRP的状态转换，没有任何action的影响，我们在后面MDP中会考虑actions的影响

$$v(s)=R_s+\gamma \sum_{s^\prime \in S} P_{ss^\prime} v(s^\prime)$$
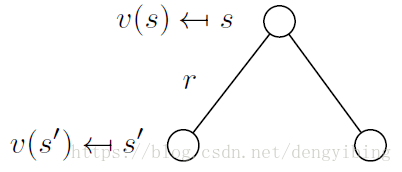
其实观察上式，上面计算的是动态规划，而注意到Bellman Equation又称为动态规划方程，上面的计算就很容易理解了

---

A Markov decision process (MDP) is a Markov reward process with decisions. It is an environment in which all states are Markov.
Markov Decision Process

A Markov Process (or Markov Chain) is a tuple $\langle S,\color{red}{A},P,R,\gamma \rangle$

• S is a (finite) set of states
• A is finite set of actions
• P is a state transition probability matrix, $P^{\color{red}{\text{a}}}_{ss^\prime}=\mathbb{P}[S_{t+1}=s^\prime|S_t=s, A_t=\color{red}{\text{a}}]$
• R is a reward function, $R^\color{red}{\text{a}}_s=E[R_{t+1}|S_t=s, A_t=\color{red}{\text{a}}]$
• $\gamma$ is a discount factor, $\gamma \in [0,1]$

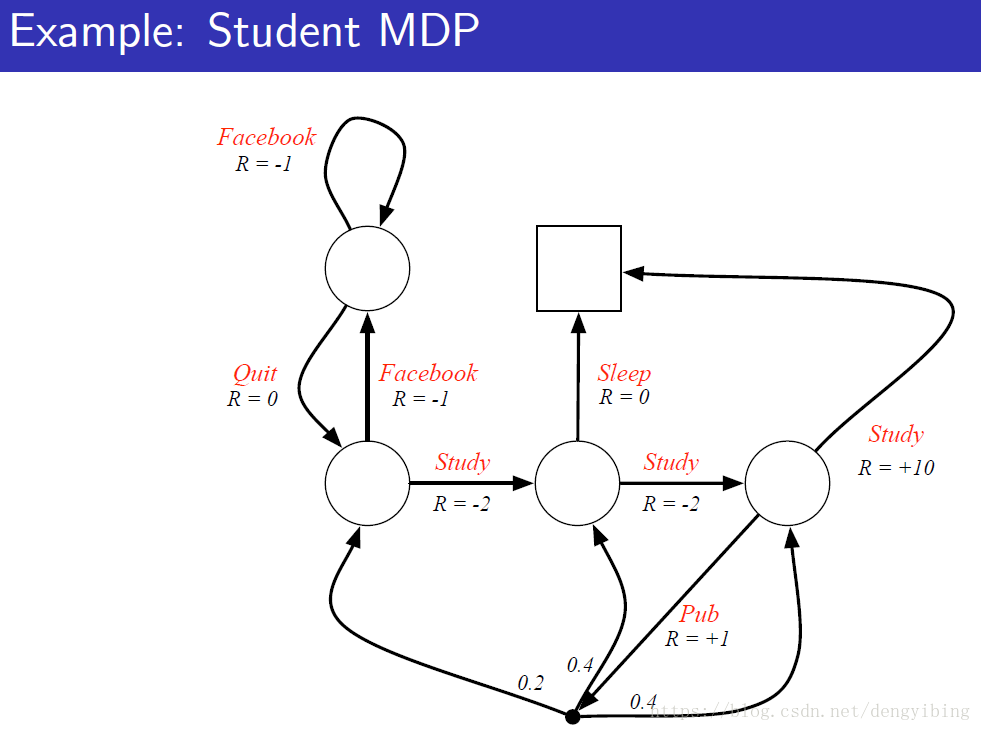
注意与上面MRP的区别，这里的黑点是执行一个action之后到达的中间状态，后面用$q(s,a)$来定义此状态，黑点到达后面的状态$s^\prime$的概率就是上面MDP中定义的那个$P^a_{ss^\prime}=\mathbb{P}[S_{t+1}=s^\prime|S_t=s, A_t=a]$

Policy

A policy $\pi$ is a distribution over actions given states,

$$\pi(a|s)=\mathbb{P}[A_t=a|S_t=s]$$

• A policy fully defines the behaviour of an agent
• MDP policies depend on the current state (not the history)
• i.e. Policies are stationary (time-independent), $A_t \sim \pi(\cdot |S_t), \forall t \gt 0$
• Given an MDP $M=\langle S,A,P,R,\gamma \rangle$ and a policy $\pi$
• The state sequence $S_1,S_2,\cdots$ is a Markov reward process $\langle S,P^{\pi} \rangle$
• The state and reward sequence $S_1,R_2,S_2,\cdots$ is a Markov reward process $\langle S,P^{\pi},R^{\pi},\gamma \rangle$
• where
  $$P^\pi_{s,s^\prime}=\sum_{a \in A} \pi(a|s)P^a_{ss^\prime}\\ R^\pi_s=\sum_{a \in A} \pi(a|s)R^a_s$$

要特别注意policy的distribution的定义，因为在后面讲的off-policy方法的概念中，生成样本的policy和目标policy是不同的

Value Function这个是针对MDP的

The state-value function $v_{\pi}(s)$ of an MDP is the expected return starting from state $s$, and then following policy $\pi$

$$v_{\pi}(s)=\mathbb{E}_{\pi}[G_t|S_t=s]$$

The action-value function $q_{\pi}(s,a)$ is the expected return
starting from state $s$, taking action $a$, and then following policy $\pi$

$$q_{\pi}(s|a)=\mathbb{E}_{\pi}[G_t|S_t=s,A_t=a]$$

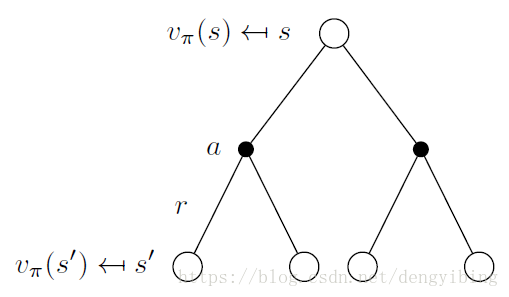
Bellman Expectation Equation for $V^{\pi}$

$$v_{\pi}(s)=\sum_{a \in A} \pi(a|s)q_{\pi}(s,a)$$
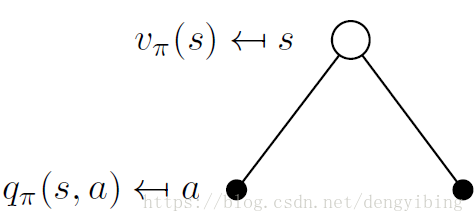
Bellman Expectation Equation for $Q^{\pi}$

$$q_{\pi}(s,a)=R^a_s+\gamma \sum_{s^\prime \in S}P^a_{ss^\prime} v_{\pi}(s^\prime)$$

$$v_{\pi}(s)=\sum_{a \in A} \pi(a|s)(R^a_s+\gamma\sum_{s^\prime \in S} P^a_{ss^\prime} v_{\pi}(s^\prime))$$

$$q_{\pi}(s,a)=R^a_s+\gamma \sum_{s^\prime \in S}P^a_{ss^\prime} \sum_{a^\prime \in A} \pi(a^\prime|s^\prime)q_{\pi}(s^\prime,a^\prime)$$

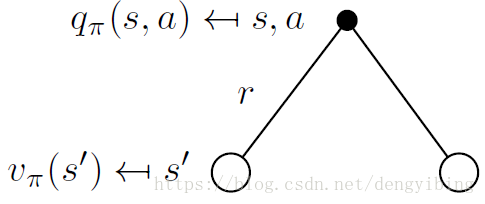
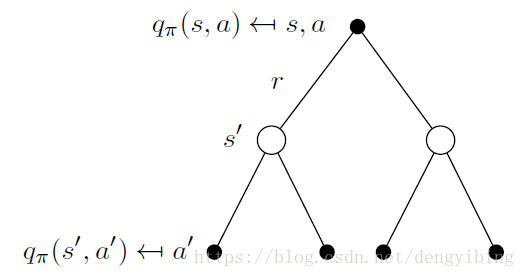
Optimal Value Function

The optimal state-value function $v_*(s)$ is the maximum value function over all policies

$$v_*(s)=\underset{\pi}{\max} v_{\pi}(s)$$

The optimal action-value function $q_*(s,a)$ is the maximum action-value function over all policies

$$q_*(s,a)=\underset{\pi}{\max} q_{\pi}(s,a)$$

只要知道了$q_*$问题就解决了，比知道$v_*$更方便。还有注意的是，上面是在所有的$\pi$(policy)中选择使得 $q$ 最大的$\pi$(policy)，这就是值给出了最佳policy的概念，当然是没有很直接的办法得到结果的，后面将针对上述问题介绍各种逼近的方法

Optimal Policy
Dene a partial ordering over policies

$$\pi \geq \pi^\prime \ \text{if}\ v_{\pi}(s) \geq v_{\pi^\prime}(s), \forall s$$

Finding an Optimal Policy
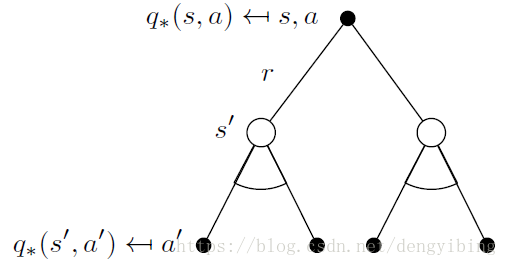
An optimal policy can be found by maximising over $q_*(s,a)$,

$$\pi_*(a|s)= \begin{cases} 1 & \text{if a = }\underset{a\in A}{arg\max} q_*(s,a)\\ 0 & \text{otherwise} \end{cases}$$
如果我们知道了$q_*(s,a)$，那么我就可以马上得到optimal policy

Optimal Bellman Expectation Equation

$$\begin{align*} v_{\pi}(s) & \doteq \mathbb{E}_{\pi}[G_t|S_t=s] \\ & = \mathbb{E}_{\pi}[\sum_{k=0}^\infty{\gamma^k R_{t+k+1}|S_t=s}] \\ & = \sum_a \pi(a|s) \sum_{s^\prime}\sum_r p(s^\prime ,r|s,a)[r+\gamma \mathbb{E}_{\pi}[G_{t+1}|S_{t+1}=s^\prime]] \\ & = \sum_a \pi(a|s) \sum_{s^\prime, r} p(s^\prime ,r|s,a)[r+\gamma v_{\pi}(s^\prime)], \text{ for all $s \in S$} \end{align*}$$

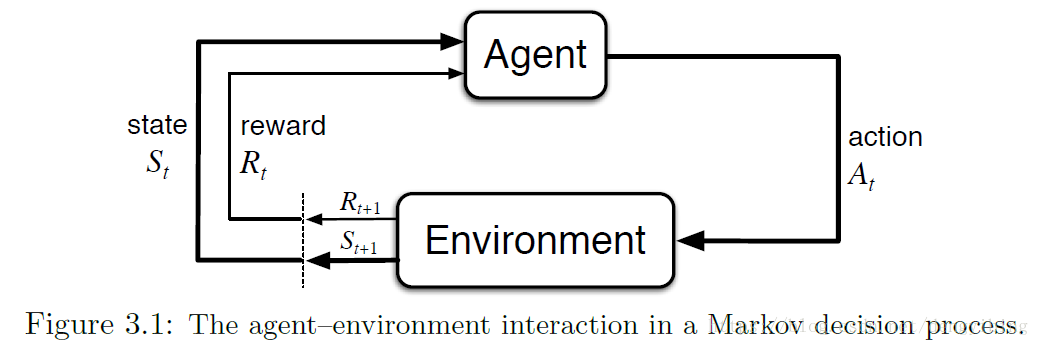
The Agent-Environment Interface

• The learner and decision maker is called the agent.
• The thing it interacts with, comprising everything outside the agent, is called the environment.

MDP和agent一起生成的sequence或者trajectory

$$S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, R_3,\cdots$$

以下函数定义了MDP的动态性，agent处于某个状态s，在该状态下采取行动a，然后到达状态$s^\prime$，并获得奖励r。这个公式是MDP的关键。这个四参数的函数可以推导出任何东西

$$p(s^\prime,r|s,a) \doteq \Pr\{S_t=s^\prime,R_t=r|S_{t-1}=s,A_{t-1}=a\}$$

for all $s^\prime$, $s\in S$, $r\in R$, and $a\in A(s)$

其中有

$$\sum_{s\prime \in S}\sum_{r\in R}p(s^\prime,r|s,a)=1, \text{ for all $s\in S$, $a \in A(s)$}$$

3.2 Goals and Rewards

agent的目的就是最大化它收到的全部rewards

3.5 Policies and Value Functions

state-value function for policy $\pi$

$$\begin{align*} v_{\pi}(s) & \doteq E_{\pi}[G_t|S_t=s] \\ & = E_{\pi}[\sum_{k=0}^\infty{\gamma^k R_{t+k+1}|S_t=s}] \\ & = \sum_a \pi(a|s) \sum_{s^\prime}\sum_r p(s^\prime ,r|s,a)[r+\gamma E_{\pi}[G_{t+1}|S_{t+1}=s^\prime]] \\ & = \sum_a \pi(a|s) \sum_{s^\prime, r} p(s^\prime ,r|s,a)[r+\gamma v_{\pi}(s^\prime)], \text{ for all $s \in S$} \end{align*}$$

action-value function for policy $\pi$

$$q_{\pi}(s,a) \doteq E_{\pi}[G_t|S_t=s,A_t=a]=E_{\pi}[\sum_{k=0}^\infty{\gamma^k R_{t+k+1}|S_t=s,A_t=a}]$$

对于任何policy $\pi$和任何状态$s$，state-value和其可能的后继状态的state-value之间存在以下一致性条件

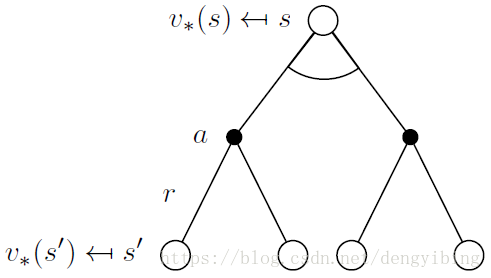
3.6 Optimal Policies and Optimal Value Functions

optimal state-value function

$$v_*(s) \doteq \underset{\pi}{\max} v_{\pi}(s)$$
optimal action-value function

$$q_*(s,a) \doteq \underset{\pi}{\max} q_{\pi}(s,a)$$

写出关于$v_*$的$q_*$

$$q_*(s,a) = E[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_t=s,A_t=a]$$

Bellman optimality equation

$$v_*(s) = \underset{a \in A(s)}{\max} q_{\pi_*}$$

---

$$\begin{align*} v_*(s) & = \underset{a \in A(s)}{\max} q_{\pi_*}(s,a) \\ & = \underset{a}{\max} E_{\pi_*}[G_t|S_t=s,A_t=a] \\ & = \underset{a}{\max} E_{\pi_*}[R_{t+1}+\gamma G_{t+1}|S_t=s,A_t=a] \\ & = \underset{a}{\max} E[R_{t+1}+\gamma v_*(S_{t+1})|S_t=s,A_t=a] \\ & = \underset{a}{\max} \sum_{s^\prime ,r} p(s^\prime,r|s,a)[r+\gamma v_*(s^\prime)] \end{align*}$$

---

$$\begin{align*} q_*(s,a) & = E[R_{t+1}+\gamma \underset{a^\prime}{\max} q_*(S_{t+1},a^\prime)|S_t=s,A_t=a] \\ & = \sum_{s^\prime ,r} p(s^\prime,r|s,a)[r+\gamma \underset{a^\prime}{\max} q_*(s^\prime, a^\prime)] \end{align*}$$