无线通信信道建模：时变与多径模型详解与比较（以及接收信号什么情况下能做N点FFT）

在无线通信的各个应用场景下，对无线信道建模往往是开展研究的第一步。

然而，对于无线信道建模的方式有多种多样。在什么条件下，该选择什么样的建模方式让人头疼。太复杂的建模难以推进研究，太简化的模型又无法表达信道特性。

本文针对$h(\tau )$、$h(t,\tau )$、$h(n)$、$\sum h_i(t)$、$\sum h_i(\tau )$、$H$（Töplitz矩阵）等多种常见的无线信道建模方式进行一一解析，分析其应用场景的全面性，从覆盖场景的全面化角度重新排序。

此外，还针对经典的问题**“时域卷积=频域乘积”**进行讨论：

接收信号$y=h\ast x+n$究竟在什么条件下，可以无失真的表示为$Y=HX+N$

一、无线信道建模

以下信道模型按全面性降序排列

① $h(t,\tau )$——时变信道冲激响应

$h(t,\tau )$是时变信道的冲激响应，表示信道在时间 $t$ 和时延 $\tau$ 上的响应。是最全面的模型
输出信号：$$y(t)=x(t)\ast h(t,\tau )=\int x(t-\tau )h(t,\tau )d\tau$$

$h(t,\tau )$是关于时间 $t$ 和时延 $\tau$ 的二维函数，该怎么理解呢？

• 在每个时刻$t_0$，信道响应$h(t_0,\tau )$随着不同径的时延$\tau$的变化都不同，捕获了多径效应
• 对于任意一条径${\tau }_0$，信道响应$h(t,{\tau }_0)$随着时间$t$的变化而变化，捕获了时变效应

② ${\sum }_i{h}_i(t)\delta (\tau -{\tau }_i)$——时变多径信道

${\sum }_i{h}_i(t)\delta (\tau -{\tau }_i)$是时变信道的离散多径模型，增益 $h_i(t)$ 随时间变化，时延 ${\tau }_i$ 固定。
输出信号：
$$y(t)=\sum _i{h}_i(t)x(t-{\tau }_i)$$
${\sum }_i{h}_i(t)\delta (\tau -{\tau }_i)$是$h(t,\tau )$的一种特例，它表示信道的多径是有限且固定的，每条路径的增益随时间变化。

③ $h(\tau )$——时不变信道冲激响应

$h(\tau )$表示时不变信道的冲激响应，仅依赖时延 $\tau$，它表示，无论时间$t$如何变化，信道在每条径上的响应都是不变的。

输出信号：
$$y(t)=x(t)\ast h(\tau )=\int x(t-\tau )h(\tau )d\tau$$

$h(\tau )$是时变信道冲激响应模型$h(t,\tau )$的一个特例，是从时变变成了时不变。

适用于固定或慢变信道。描述多径传播但不考虑时间变化。

④ ${\sum }_i{h}_i\delta (\tau -{\tau }_i)$——时不变多径信道

${\sum }_i{h}_i\delta (\tau -{\tau }_i)$是时不变信道的离散多径模型，增益 $h_i$ 固定，时延 ${\tau }_i$ 离散

输出信号：
$$y(t)=\sum _i{h}_{i}x(t-{\tau }_i)$$

${\sum }_i{h}_i\delta (\tau -{\tau }_i)$是 $h(\tau )$的一种特例，它表示信道的多径是有限且固定的，每条路径的增益固定。

⑤ $h(n)$——离散时间信道冲激响应

$h(n)$是$h(\tau )$的离散化版本，适用于数字通信系统，依赖离散时间 $n$。
输出信号：
$$y(n)=\sum _{k}x(n-k)h(k)$$
由于离散化的原因，$h(n)$不能表示连续时延$\tau$的多径，受到采样间隔$T_s$的影响，它能表示的多径时延只能是采样间隔$T_s$的整数倍，无法表示小数倍。

⑥ $\mathbf{H}$——离散时间卷积矩阵

$\mathbf{H}$ 是基于 $h(n)$ 构建的Töplitz矩阵，表示离散时间信道的卷积操作，适用于线性时不变系统。

输出信号：
$$\mathbf{y}=\mathbf{H}\mathbf{x}+\mathbf{n}$$
$$\left[\begin{array}{c}y(1)\\ y(2)\\ \cdot \cdot \cdot \\ y(N)\end{array}\right]=\left[\begin{array}{cccc}h(1)& 0& \cdot \cdot \cdot & 0\\ h(2)& h(1)& \cdot \cdot \cdot & 0\\ \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot \\ h(N)& h(N-1)& \cdot \cdot \cdot & h(1)\end{array}\right]\left[\begin{array}{c}x(1)\\ x(2)\\ \cdot \cdot \cdot \\ x(N)\end{array}\right]$$

这么一看是不是很直观，把复杂的卷积运算换成矩阵乘法，方便处理。不过我这个写法还不对，这么写漏掉了前一个信号的拖尾效应。因为卷积是会拉长信号长度的，这么写成矩阵的形式就有偏差，严谨的写法如下：


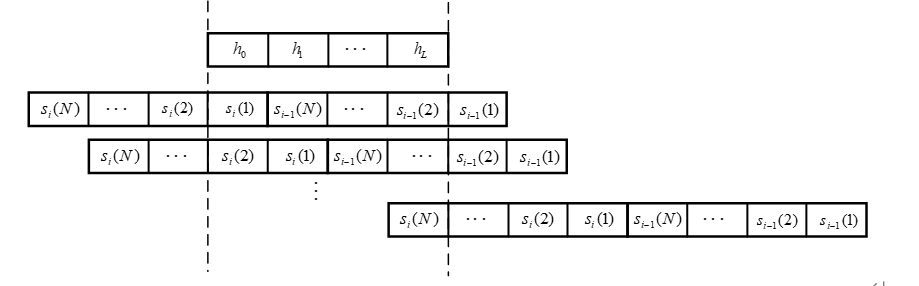
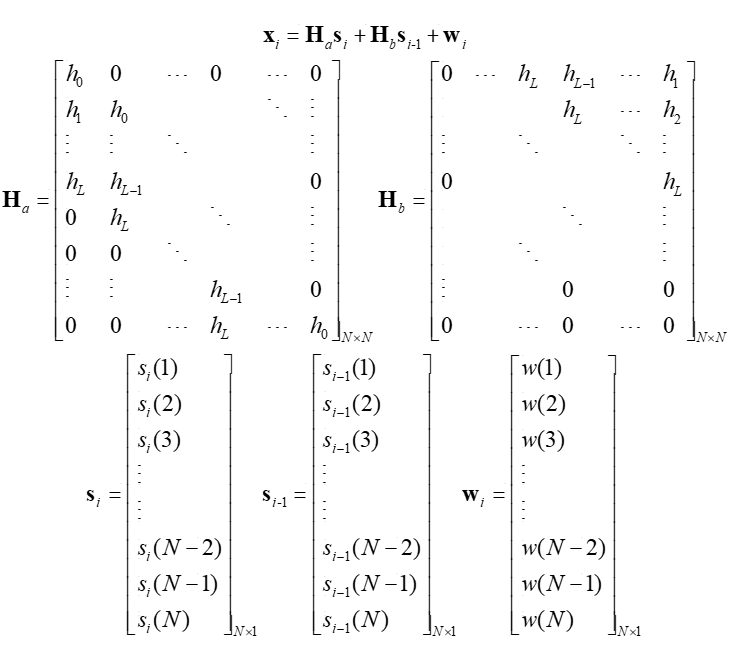
其中，${\mathbf{H}}_a$为 信道矩阵，表示信道对第i个周期信号的影响， ${\mathbf{H}}_b$也是 信道矩阵，表示信道对第i-1个周期信号 造成的拖尾影响。
则一组接收信号中既包含了当前周期目标信号的成分，也包含了前一个周期的信号 的成分，这是多径衰落信道中不可避免的多径干扰。

有点复杂，不过好处是做FFT的时候，信道矩阵可以对角化，此处不再赘述。

总结与比较

总结

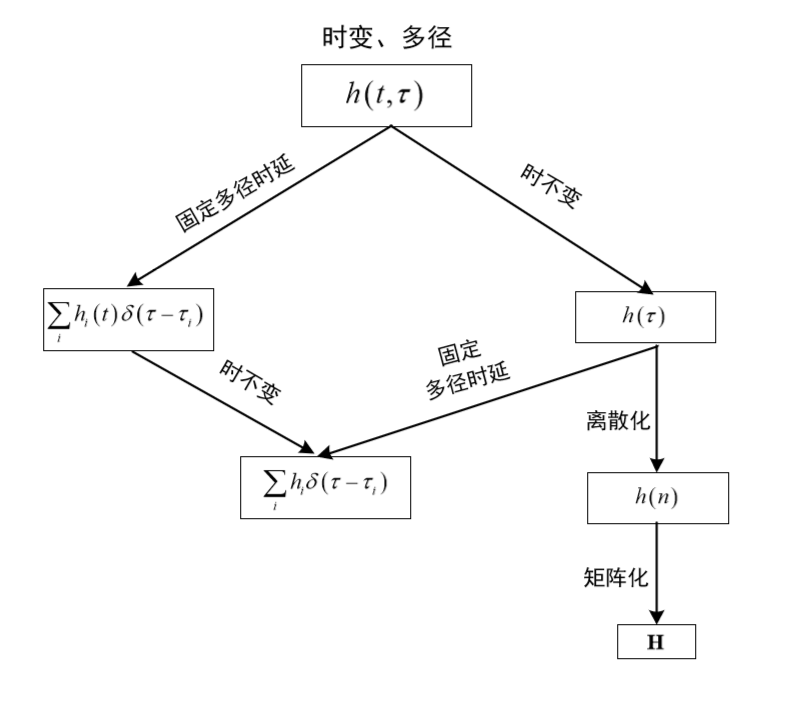
比较

序号	信道模型	适用性	模型说明	局限性
1	$h(t,\tau )$	适合高速移动通信场景，如5G、UWB、复杂时变信道	描述信号在时间t和时延τ上的响应，适用于时变信道	模型复杂，计算成本高
2	${\sum }_i{h}_i(t)\delta (\tau -{\tau }_i)$	适合高速移动通信场景，如城市移动通信、瑞利衰落	描述时变信道中离散多径分量的时变增益	假设时延固定，无法描述连续时延分布
3	$h(\tau )$	适合固定或慢变信道，如室内Wi-Fi、有线信道	描述时不变信道的时延响应，适用于多径传播	无法描述时变特性
4	${\sum }_i{h}_i\delta (\tau -{\tau }_i)$	适合城市环境固定无线通信，如GSM、CDMA	描述时不变信道中的离散多径分量	仅限于离散多径，无法描述连续时延
5	$h(n)$	适合数字通信系统，如OFDM、数字基带处理	离散时间域的信道冲激响应，基于采样	受限于采样精度
6	$\mathbf{H}$ (Töplitz矩阵)	适合MIMO、信道均衡等矩阵运算场景	基于h(n)构建的Töplitz矩阵，表示离散卷积	仅适用于LTI系统，应用特定

二、接收信号能否直接做N点FFT

对这样一个离散接收信号模型：
$$y(n)=x(n)\ast h(n)=\sum _{k=1}^{L}x(n-k)h(k)$$

信号长度N，信道长度L，输出长度N+L-1。即经过信道，信号被拉长了。

根据线性时不变系统的“时域卷积=频域乘积”的理论
(注意，一定要是线性时不变系统，所以信道响应必须是时不变的)
应该有：
$$Y(k)=x(k)\cdot h(k)$$

信号$x(n)$与信道响应$h(n)$的卷积*是线性卷积，因此输出$y(n)$ 的长度会变长至N+L-1
理论上，接收信号要做N+L-1点的FFT才能保证频谱不失真，那什么情况下能做N点FFT，强行做N点FFT又有什么影响?

周期信号

做N点FFT就是默认将线性卷积变为N点的循环卷积，这就涉及到一个重要知识

循环卷积假设信号在长度 $M$ 的窗口内是周期性的。
我们知道，如果$M\ge N+L-1$，循环卷积输出与线性卷积一致,无失真。

但是如果$M＜N+L-1$呢？此时需要分情况讨论

如果$x(n)$是周期信号，$M=L$点循环卷积在一个周期内等价于线性卷积，无失真。（OFDM通过添加CP实现伪周期性，从而应用循环卷积）
如果$x(n)$是非周期信号，$M＜N+L-1$点循环卷积就会导致时间域混叠，出现失真

因此周期信号，以及添加了循环前缀CP的OFDM信号满足循环卷积的条件，可以直接做N点的FFT，并且频谱不失真。

非周期信号

经过刚刚的分析，我们知道非周期信号不满足循环卷积的条件，必须对N+L-1点的线性卷积进行FFT才能保证不失真。

如果强行做N点FFT，就需要从接收信号中丢弃L-1个样本，这会导致频谱出现怎样的失真？

假设取 $y_{\text{lin}}[n]$ 的前 $L$ 点，定义截断信号：
$$y_{\text{trunc}}[n]=\{\begin{array}{ll}{y}_{\text{lin}}[n],& 0\le n\le N-1\\ 0,& \text{otherwise}\end{array}$$

这等价于对 $y_{\text{lin}}[n]$ 施加矩形窗 $w[n]$（长度 $N$）：
$$y_{\text{trunc}}[n]=y_{\text{lin}}[n]\cdot w[n],w[n]=\{\begin{array}{ll}1,& 0\le n\le N-1\\ 0,& \text{otherwise}\end{array}$$

在频域中，窗函数 $w[n]$ 的 DTFT $W(f)$ 与 $Y_{\text{lin}}(f)$ 卷积：
$$Y_{\text{trunc}}(f)=Y_{\text{lin}}(f)\ast W(f)$$
$W(f)$ 是矩形窗的频谱（类似 sinc 函数），具有主瓣和旁瓣，导致频谱展宽和泄漏。

频谱具体来说会出现如下失真：

• 频谱展宽：截断相当于施加矩形窗，$Y_{\text{trunc}}(f)$ 的频谱被 $W(f)$ 的主瓣展宽，主瓣宽度约为 $2/(N{T}_s)$。这使得 $Y[k]$（$N$ 点 FFT 的结果）在每个频率点包含来自邻近频率的贡献，降低频率分辨率。
• 旁瓣泄漏：矩形窗的旁瓣导致频谱能量泄漏到其他频率分量，尤其在 $y_{\text{lin}}[n]$ 的尾部（$n=N,\dots ,N+L-2$）包含显著能量时，泄漏更明显。 幅度失真：由于丢失了尾部 $L-1$ 个样本，$Y[k]$ 的幅度可能偏离真实频谱 $Y_{\text{lin}}(f)$，特别是在低频和高频区域。
• 相位失真：截断可能改变 $y_{\text{lin}}[n]$ 的时间结构，导致 $Y[k]$ 的相位信息不准确，影响相位敏感的应用（如相干检测）。

频谱的失真从时域上来等效观察，相当于时间域混叠。

如果直接对 $x[n]$ 和 $h[n]$ 进行 $N$ 点循环卷积，等价于将尾部的L-1个样本折叠到开头。

结论

1. 如果信道响应h(n)长度为L=1，无论什么信号都可以直接做N点FFT
2. 如果信道响应h(n)长度L>1，周期信号可以做N点FFT，也可以做N+L-1点FFT，后者频谱分辨率更高。
3. 如果信道响应h(n)长度L>1，非周期信号可以做N+L-1点FFT保证不失真，也可以通过添加CP 将非周期信号的线性卷积转化为循环卷积，做N点FFT。但是如果直接做N点FFT，就会使得频谱展宽，旁瓣泄露。
4. 核心差异在于：非周期信号的线性卷积扩展了输出长度，而周期信号的周期性和 OFDM 的 CP 机制限制了输出长度为 $L$，从而简化 FFT 点数需求。