操作定律：性能分析与设备优化,-优快云博客

本文链接：https://blog.youkuaiyun.com/dcjszhr/article/details/133362196

操作定律

操作定律（1）

• 排队网络中性能指标的平均值

• 不对服务时间或到达间隔的分布做出假设

• 操作平均值是直接测量得出的

• 操作数量在有限的观察期间内直接测量得出

• 操作定律是操作数量之间的关系

操作定律（2）

• 考虑设备i（或服务中心i）的黑箱视图：

如果我们观察设备一段有限的时间T（观察期），我们可以测量：

工作到达的数量（Ai）
在此期间设备i的忙碌时间（Bi）
工作离开的数量（Ci）

操作定律（3）

• 可以得出更多的操作数量：

■ 到达率 $\lambda_i = \frac{A_i}{T}$

■ 吞吐量 $X_i = \frac{C_i}{T}$

■ 利用率 $U_i = \frac{B_i}{T}$

■ 其中 i=0（系统）且 i > 0（设备）

■ 每个工作访问队列i的平均服务时间， $S_i = \frac{B_i}{C_i}$

■ 在离开系统之前，工作访问设备i的平均次数 $V_i$

对于一个给定的任务，disk1和disk2被访问了不止一次。

任务遵循预定的路线：CPU，disk1，disk2，disk1，disk2，然后退出（离开系统）。

利用率定律 $(U_i=X_iS_i=\lambda_iS_i=XD_i)$

• $U_i = \frac{B_i}{T} \times \frac{C_i}{C_i} = \frac{C_i}{T} \times \frac{B_i}{C_i} = X_i S_i$

例子：数据包以每秒125个的速度离开一个网关，该网关处理每个数据包的平均时间为2毫秒。

$U_i = 125 * 0.002 = 0.25$

• 工作流平衡假设：设备i，在观察周期T中，工作到达的数量（Ai）等于工作完成的数量（Ci）。

■ 假设工作流平衡，则 $A_i = C_i \ or \ \frac{A_i}{T} = \frac{C_i}{T} \ or \ U_i = \lambda_i S_i$

• 利用率定律： $U_i = X_i S_i = \lambda_i S_i$

■ 利用率最大的设备是瓶颈设备。

强制流定律 $(X_i = X V_i)$

• 将系统吞吐量与各个设备的吞吐量相关联

• 每个设备满足工作流平衡，即 $A_i = C_i$

• 设 X 为系统吞吐量

■ 对于开放网络，单位时间离开系统的工作数量

■ 对于封闭网络，离开系统重新进入的工作数量

• 设 $C_0$ 为在 T 中离开系统的工作数量，那么 $X = \frac{C_0}{T}$

• 当在设备 i 处工作流平衡时， $V_i = \frac{C_i}{C_0}$ ，其中 $V_i$ 被称为访问比率

• 设备 i 的吞吐量为 $X_i = \frac{C_i}{T} \times \frac{C_0}{C_0} = X V_i$

访问比率或每个工作到设备 i 的访问次数

• 每个工作对系统中的第 i 个设备提出 $V_i$ 个请求。

• 如果工作流平衡，工作到达的数量等于工作完成的数量（ $C_0$ ）。

• 因此，访问第 i 个设备的工作数量 $C_i$ 是： $C_i = C_0 V_i \ or \ V_i = \frac{C_i}{C_0}$

• $V_i$ 因此是到第 i 个设备和外部链接（工作完成）的访问比率。

• 对于一个工作： $V_i = \frac{C_i}{1} =$ 每个工作到设备 i 的访问次数

• 例子：

■ $C_{{disk1}} = C_0 V_{{disk1}} \ or \ V_{\text{disk1}} = \frac{C_{\text{disk1}}}{C_0}$

■ 对于一个工作， $V_{\text{disk1}} = \frac{C_{\text{disk1}}}{1}$

■ 对于十个工作， $C_{{disk1}}=20$ ； $V_{\text{disk1}} = \frac{20}{10}=2$

强制流定律(续)

• 如果 $D_i$ 是一个工作在设备 i 的总服务需求，那么 $D_i = V_i S_i$

• 接下来，结合强制流定律和利用率定律，我们有 $U_i = X_i S_i = X V_i S_i = X D_i$

• $P_{ij}$ 表示一个工作在设备 i 完成服务后移动到设备 j 的概率， $P_{00} = 0$

• 在一个具有工作流平衡的系统中（假设系统中有 M 个设备） $C_j= \sum^M_{i=0}C_iP_{ij}$

• 两边同时除以 $C_0$ ，我们得到 $V_j= \sum^M_{i=0}V_iP_{ij}$

• 这组方程与 $V_0 = 1$ 一起被称为访问比率方程。

示例 1：操作定律

一个分时计算机系统的会计日志为用户程序生成了以下概况。每个程序需要 5 秒的 CPU 时间，并向磁盘 A 发出 80 个 I/O 请求，向磁盘 B 发出 100 个 I/O 请求。用户的平均思考时间是 18 秒。从设备规格中，确定磁盘 A 满足一个 I/O 请求需要 50 毫秒，磁盘 B 每个请求需要 30 毫秒。有 17 个活动终端时，观察到磁盘 A 的吞吐量为每秒 15.7 个 I/O 请求。确定系统吞吐量和设备利用率。

系统吞吐量，X=? 设备利用率： $U_{cpu},U_A,U_B=?$

(1)从强制流定律：

$X_A = X \cdot V_A \\ X = \frac{X_A}{V_A} = \frac{15.7 }{80} = 0.1963 \ \ job/second$

(2)

$U_{\text{CPU}} = X \cdot D_{\text{CPU}} = 0.1963 \cdot 5 = 98\%\\ U_A = X_A \cdot S_A = 15.7 \cdot 0.05 = 78.5\% \\ U_B = X_B \cdot S_B= X_B \cdot 0.03= XV_B \cdot 0.03 = 0.1963 \cdot 100 \cdot0.03=58.9 \%$

Little定律

• 假设工作流平衡

• 如果 $Q_i$ 是队列 i 的平均队列大小，而 $R_i$ 是队列 i 处的平均客户响应时间，那么： $Q_i = \lambda_i R_i = X_i R_i$

示例2 ：操作定律

如果队列长度为： $Q_{CPU}=8.88 ; \ Q_{A}=3.19; \ Q_B=1.4$

确定设备响应时间 $X_{\text{CPU}} = X V_{\text{CPU}} = 0.1963 \times 181 = 35.48$

$X_{\text{CPU}} = 35.53, \quad X_A = 15.7, \quad X_B = 19.6$

使用Little定律，设备响应时间为：

$R_{CPU}=\frac{Q_{CPU}}{X_{CPU}}=\frac{8.88}{35.53}=0.25s\\ R_{A}=\frac{Q_{A}}{X_{A}}=0.203s\\ R_{B}=\frac{Q_{B}}{X_{B}}=0.071s$

通用响应时间定律

• 只要系统的某一部分的工作流是平衡的，Little定律就可以应用到系统的任何部分。

• 因此，Q=XR，其中Q是系统中的平均数量，R是系统中的平均客户响应时间。

• 由于 $Q= Q_1+...+Q_M$ ; $XR = \sum^M_{i=1}X_iR_i$

• 两边同时除以X并使用强制流定律： $R=\sum^M_{i=1}V_iR_i$

交互响应时间定律

• 在一个交互系统中，用户生成一个请求并等待响应；在收到响应后，等待一段时间（思考时间）并生成下一个请求。

• 设R为系统响应时间，Z为平均思考时间。

• 因此，在时间周期T中，每个用户生成 T/(R+Z) 的请求。

• 对于N个用户（终端），

■ 完成的工作数量 = N∗T/(R+Z)

■ 系统吞吐量 X=(NT/(R+Z))/T = N/(R+Z) 或 R=N/X−Z

示例3：操作定律

X=0.1963，N=17 且 Z=18

$R = \frac{17}{0.1963} - 18 = 686s$

操作定律（总结）

• 利用率定律

$U_i = X_i S_i = \lambda_i S_i = X D_i \ \ where \ \ \ D_i = V_i S_i$

• 强制流定律

$X_i = X V_i$

• Little定律

$Q = XR \ (system) \ \ or \ \ Q_i = \lambda_i R_i = X_i R_i \ \ (device \ i)$

• 一般响应时间定律

$R=\sum^M_{i=1}V_iR_i$

• 交互响应时间定律

$R = \frac{N}{X} - Z$

性能界限

• 为什么要进行界限分析？

• 提供了对影响性能的主要因素的洞察，例如，识别和量化瓶颈的程度。

• 提供了一种初步的建模技术，用于在研究的早期阶段消除不足的替代方案。

• 渐近界限：确定上界和下界，例如，系统吞吐量和响应时间作为系统工作负载强度的函数。

• 平衡界限：当设备需求平衡时的性能，即，没有瓶颈。

渐近界限

• 例子：

■ 乐观（吞吐量）和悲观（响应时间）界限

■ 如何 - 考虑轻和重负载的极端条件

• 界限的有效性仅依赖于一个单一的假设：客户在中心的服务需求不依赖于系统中当前有多少其他客户，或者他们位于哪些服务中心。

• 从强制流定律可知，设备利用率与总服务需求成正比： $U_i \propto D_i$

■ 因此，具有最高总服务需求 $D_i$ 的设备具有最高的利用率，并且是瓶颈设备。

■ 如果设备 b 是瓶颈，那么 $D_b = D_{\text{max}}$ 是 $D_1, D_2, \ldots, D_m$ 中最高的。

• 渐近界限：

■ 系统吞吐量 $X(N) \leq \min \left\{ \frac{1}{D_{\text{max}}}, \frac{N}{D + Z} \right\}$ （上界）

■ 系统响应时间 $R(N) \geq \max \left\{ D, ND_{\text{max}} - Z \right\}$ （下界）

■ 其中，D 是除终端外所有设备上的总服务需求（所有服务需求的总和）

• 基于以下观察：

任何设备的利用率不能超过1。这对可获得的最大吞吐量设定了一个限制 - 上界。
带有N个用户的系统的响应时间不能少于只有一个用户的系统。这对最小响应时间设定了一个限制 - 下界。
使用交互响应时间公式。

界限推导：

• 对于瓶颈设备b我们有： $U_b = XD_{\text{max}}$ （利用率定律）

• 由于 $U_b \leq 1$ ，所以 $XD_{\text{max}} \leq 1$ ，因此 $X \leq \frac{1}{D_{\text{max}}}$ （1）

• 对于一个作业，所有队列的等待时间都是零， $R=\sum_{i=1}^MD_i=D$

• 对于多于一个用户 $R \geq D$ （2）

• 将交互响应时间定律与不等式（1）结合，我们得到 $R(N) \geq ND_{\text{max}} - Z$ （3）

• 结合（2）和（3）-界限， $R(N) \geq \max(D, ND_{\text{max}} - Z)$ （4）

• 将交互响应时间定律与不等式（2）结合，我们得到 $X(N) \leq \frac{N}{D + Z}$ （5）

• 结合（1）和（5）-界限， $X(N) \leq \min\left(\frac{1}{D_{\text{max}}}, \frac{N}{D + Z}\right)$ （6）

• 对于批量工作负载，Z=0。

渐近界限（续）：

• $D = ND_{\text{max}} - Z$ 或者 $N^* = \frac{D + Z}{D_{\text{max}}}$ （在拐点的用户数量） $> N^*$ （排队）

• 对于 $N < N^*$ ，当 N 增加时，响应时间不会显著增加，而吞吐量增加非常快。

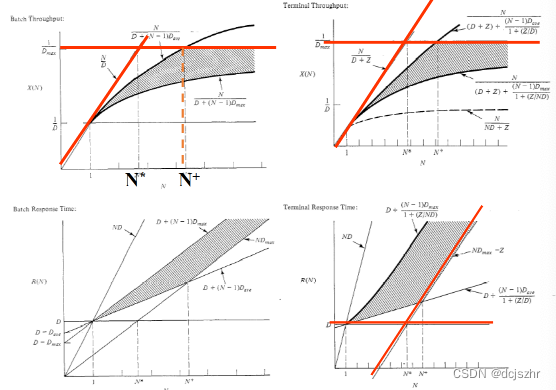
渐近界限（总结）

• 渐近界限：

■ 系统吞吐量（上界）： $X(N) \leq \min \left\{ \frac{1}{D_{\text{max}}}, \frac{N}{D + Z} \right\}$

■ 系统响应时间（下界）： $R(N) \geq \max \left\{ D, ND_{\text{max}} - Z \right\}$

■ 在拐点的用户数量： $N^* = \frac{D + Z}{D_{\text{max}}}$

• 平衡系统界限：

$\frac{N}{D + (N - 1)D_{\text{max}}} \leq X(N) \leq \min \left( \frac{1}{D_{\text{max}}}, \frac{N}{D + (N - 1)D_{\text{ave}}} \right) \\ \max(ND_{\text{max}}, D + (N - 1)D_{\text{ave}}) \leq R(N) \leq D + (N - 1)D_{\text{max}}$

示例4：渐近界限（1）

$D_{\text{CPU}} = 5, \quad D_A = 4, \quad D_B = 3, \quad Z = 18 \\ D = D_{\text{CPU}} + D_A + D_B = 12 \\ D_{\text{max}} = D_{\text{CPU}} = 5$

∴渐近界限是：

$X(N) \leq \min \left( \frac{N}{D+Z}, \frac{1}{D_{\text{max}}} \right) =\min ( \frac{N}{30}, \frac{1}{5}\}$

$R(N) \ge max \{D,ND_{max}-Z\}=max \{12,5N-18\}$

膝部出现在： $12= 5N - 18$ ; $N^*=6$

如果系统中有超过6个用户，系统中肯定会出现排队。

示例5：渐近界限（2）

如果响应时间必须保持在100秒以下，可以支持多少终端？

由于 $R(N) \geq \max(12, 5N - 18)$ ; $100 \geq 5N - 18$ ; $N \leq 23.6$

如果所需响应时间少于100秒，系统不能支持超过23个用户。

平衡系统界限

• 更紧密的界限（补充渐近界限）

• 平衡？ $D_1 = D_2 = D_3 \ldots = D_k$

• 批处理工作负载给定在服务中心的利用率： $U_k(N) = \frac{N}{N+K-1}$

■ 其中，N = 工作数量，K = 服务中心的数量，由利用率定律（ $U_i = X D_i$ ）： $X(N) = \frac{U_k}{D_k} = \frac{N}{N+K-1} \cdot \frac{1}{D_k}$ 其中， $D_k$ = 每个中心的服务需求。

• 设 $D_{\text{max}}, D_{\text{ave}}$ 和 $D_{\text{min}}$ 分别表示最大、平均和最小的服务需求。

• 我们使用两个平衡系统的吞吐量来界定系统吞吐量：

■ a. 每个服务中心的服务需求都是 $D_{\text{min}}$

■ b. 每个服务中心的服务需求都是 $D_{\text{max}}$

• 因此， $\frac{N}{N+K-1} \times \frac{1}{D_{\text{max}}} \leq X(N) \leq \frac{N}{N+K-1} \times \frac{1}{D_{\text{min}}}$ (7)

和响应时间： $(N+K-1) D_{\text{min}} \leq R(N) \leq (N+K-1) D_{\text{max}}$ (8)

• 平衡系统界限

$\frac{N}{D+(N-1)D_{\text{max}}} \leq X(N) \leq \min \left( \frac{1}{D_{\text{max}}}, \frac{N}{D+(N-1)D_{\text{ave}}} \right)$

$\max(ND_{\text{max}}, D + (N-1)D_{\text{ave}}) \leq R(N) \leq D + (N-1)D_{\text{max}}$

示例6: 瓶颈分析

在这个例子中，保险公司正在考虑升级其分布在二十个地理位置的 IBM 3790s 系统。公司正在考虑两个替代方案，IBM 8130s 和 8140s。经过与供应商的讨论，公司认为，与 3790s 相比，8130s 能够提高 1.5 到 2 倍的性能，而 8140s 则能够提高 2 到 3.5 倍的性能。