详解mnist的LeNet实现

mnist作为深度学习的入门程序，就像其他编程语言的Hello World,掌握了如何用DL解决mnist分类问题，是每一个深度学习爱好者的必经之路。网上关于MNIST的博客有很多，这里写下自己学习的感悟，有什么出错的地方，请指教。
深度学习有两把利器，卷积神经网络CNN与循环神经网络RNN，两个都是为了更好的提取特征。CNN主要用于处理图像上，因为图像有局部相关性。而RNN通常用于自然语言处理（NLP）中，因为语音信号和时序有关。在MNIST这个图像分类问题中，我们使用卷积神经网络。
卷积神经网络（CNN）
Why CNN?
对于传统的深层神经网络，随着隐含层以及神经元数目的增加，使得训练参数暴涨，不仅使得训练时间变长，还容易造成过拟合，解决办法就是使用卷积神经网络代替传统的神经网络。CNN如何达到这个目的？有以下三大法宝：
1. 稀疏连接
前面说传统全连接神经网络要学习的权重太多，导致训练时间太久，所以在卷积神经网络中，相邻两层采用局部连接的方式来寻找输入特征的局部相关性。局部连接的神经元个数称为感受野，局部连接个数越多，感受野越大，越接近全连接神经网络。

2. 共享权值
在卷积神经网络中，不同感受野之间的权重相同，这样进一步减少了要学习的参数数量。

3. 池化（pooling）
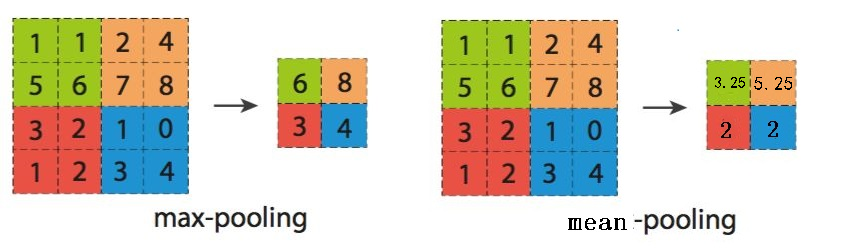
池化是将输入图像化为多个正方形区域，对于每一个小正方形，输出其中数据的最大值的池化方式被称为最大池化（max-pooling）,输出其中数据的平均值，被称为平均值池化（mean-pooling）。一般常用最大池化，池化操作相当于给图像打马赛克，效果如图。通过池化操作，进一步消除非最大值，降低计算量。


虽然花变模糊了，但依然可以分辨出来，计算量减小很多
下面介绍LeNet神经网络，LeNet是由大神Yann Lecun与1998年发表的论文提出来的，论文地址
http://www.dengfanxin.cn/wp-content/uploads/2016/03/1998Lecun.pdf
LeNe网络模型如下

这几层网络结构分别为
输入层INPUT、卷积层C1、池化层S2、卷积层C3、池化层S4、卷积层C5（全连接层）、全连接层F6、输出层OUTPUT。
卷积层
主要通过卷积核来进行图像的特征提取，过程如下图所示就是原始数据与3X3的卷积核
1 0 1
0 1 0
1 0 1
做矩阵乘法，然后以步长为1进行移动，得到卷积后的结果。LeNet中第一个卷积层使用5X5、深度为6、步长为1的卷积核，来对原始图像像素进行卷积操作。

池化层
又称为下采样层，主要是对卷积后的结果进行池化操作，以此降低网络的训练参数及模型的过拟合程度。

全连接层（F6）
计算输入向量和权重向量的点积，再加上一个偏置，随后将其传给激活函数。
输出层（OUTPUT）
LeNet中的输出层由欧式径向基（RBF）函数单元组成，每个类别对应一个径向基函数单元，每个输出RBF单元计算输入向量和该类别标记向量之间的欧式距离。距离越远，RBF输出越大。
LeNet的网络模型基本就这些，下面附代码再做详细介绍。（代码主要参考Python机器学习算法 ——赵志勇）

# -*- coding: utf-8 -*-
"""
Created on Mon Jan 29 12:49:13 2018
input输入层
卷积核为3×3的conv2d卷积层
2×2的Maxpooling池化层
卷积核为3×3的conv2d卷积层
2×2的Maxpooling池化层
卷积核为3×3的conv2d卷积层,在LeNet论文中，输入矩阵为5X5X16，卷积核为5X5，和全连接层没有区别
625的full-connect全连接层
625to10 output输出层
@author: dbsdz
"""

import tensorflow as tf
import numpy as np
import time
batch_size = 500
from tensorflow.examples.tutorials.mnist import input_data


def weight_variable(shape):
    '''
    权重初始化函数，输入维度，输出符合正太分布的变量。
    '''
    initial = tf.truncated_normal(shape, stddev=0.01)
    return tf.Variable(initial)

def bias_variable(shape):
    '''
    偏置项初始化函数，输入维度，输出初始值为0.0的偏置项
    '''
    initial = tf.constant(0.0, shape = shape)
    return tf.Variable(initial)

def conv2d(X, W):
    '''
    输入： X必须是四维张量，W为四维的卷积核，类型与X一致。
            strides，长度为四的一维整数类型数组，每一维度对应卷积核的中每一维的对应移动步数
            padding='SAME',仅适用于全尺寸操作，即输入数据与输出数据维度相同。
    输出：X与W做卷积运算后的结果
    '''
    return tf.nn.conv2d(X, W, strides=[1, 1, 1, 1], padding='SAME')
# max_pooling,窗口大小为2X2
def max_pool_2x2(X):
    '''
    输入： X是一个四维张量，维度为[batch, height, width, channels]
            ksize,长度不小于4的整型数组，每一维上的值对应于输入数据张量中每一维的窗口对应值
            strides，指定滑动窗口在输入数据在输入数据张量每一维上的步长。
    '''
    return tf.nn.max_pool(X, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
#构造卷积神经网络CNN类
class CNN():

    def __init__(self, input_data_trX, input_data_trY, input_data_vaX, \
                 input_data_vaY, input_data_teX, input_data_teY):
        self.w = None       #第一个卷积层的权重
        self.b = None       #第一个卷积层的偏置
        self.w2 = None      #第二个卷积层的权重
        self.b2 = None      #第二个卷积层的偏置
        self.w3 = None      #第三个卷积层的权重
        self.b3 = None      #第三个卷积层的偏置
        self.w4 = None      #全连接层中输入层到隐含层的权重
        self.b4 = None      #全连接层中输入层到隐含层的偏置
        self.w_o = None     #隐含层到输出层的权重
        self.b_o = None     #隐含层到输出层的偏置
        self.p_keep_conv = None     #卷积层中样本保持不变的比例
        self.p_keep_hidden = None   #全连接层中样本保持不变的比例
        self.trX = input_data_trX   #训练数据中的特征
        self.trY = input_data_trY   #训练数据中的标签
        self.vaX = input_data_vaX   #验证数据中的特征
        self.vaY = input_data_vaY   #验证数据中的标签
        self.teX = input_data_teX   #测试数据中的特征
        self.teY = input_data_teY   #测试数据中的标签
    def fit(self):
        '''
        调整输入数据placeholder的格式，输入X为一个四维矩阵
        第一维表示一个batch中样例的个数，初始为None
        第二维和第三维表示图片的尺寸，MNIST数据集中的图片为28X28
        第四维表示图片的深度，对于黑白图片，深度为1
        '''
        X = tf.placeholder(tf.float32, [None, 28, 28, 1])
        Y = tf.placeholder(tf.float32, [None, 10])

        #第一层卷积核大小为3X3，输入一张图，输出32个feature map，在LeNet模型中，卷积核为5X5，
        #但是对于28X28的图片来说，3X3的卷积核提取出的特征比5X5的要好，这样准确率也会提升。
        #权重W的数组第三个维度是图片的通道数，第四个维度是卷积核的个数，也就是深度
        #个数越多，网络越深，相应的计算复杂度也会提升，更加消耗计算资源。
        self.w = weight_variable([3, 3, 1, 32])
        self.b = bias_variable([32])
        #第二层卷积核大小为3X3，输入32个feature map,输出64个feature map
        self.w2 = weight_variable([3, 3, 32, 64])
        self.b2 = bias_variable([64])
        #第三个卷积核大小为3X3，输入64个feature map,输出128个feature map
        self.w3 = weight_variable([3, 3, 64, 128])
        self.b3 = bias_variable([128])
        # 全连接层FC 128 * 4 * 4 inputs, 625 outputs
        self.w4 = weight_variable([128 * 4 * 4, 625])
        self.b4 = bias_variable([625])
        # 全连接层FC 625 inputs, 10 outputs (labels)
        self.w_o = weight_variable([625, 10])
        self.b_o = bias_variable([10])
        self.p_keep_conv = tf.placeholder("float")      #卷积层的dropout概率
        self.p_keep_hidden = tf.placeholder("float")    #全连接层的dropout概率
        #第一个卷积层      
        l_c_l = tf.nn.relu(conv2d(X, self.w) + self.b)  #1_c_1  shape=(?,28,28,32)
        l_p_l = max_pool_2x2(l_c_l)                     #1_p_1 shape(?, 14, 14, 32)        
        #dropout:每个神经元有p_keep_conv的概率以1/p_keep_conv的比例进行归一化，
        #有（1-p_keep_conv)的概率置为0
        l1 = tf.nn.dropout(l_p_l, self.p_keep_conv)

        #第二个卷积层      
        l_c_2 = tf.nn.relu(conv2d(l1, self.w2) + self.b2)  #1_c_2 shape=(?, 14, 14, 64)        
        l_p_2 = max_pool_2x2(l_c_2)          #l_p_2 shape=(?, 7, 7, 64)
        l2 = tf.nn.dropout(l_p_2, self.p_keep_conv)

        #第三个卷积层
        l_c_3 = tf.nn.relu(conv2d(l2, self.w3) + self.b3)  #l_c_3 shape = (?, 7, 7,128)
        l_p_3 = max_pool_2x2(l_c_3)         #1_p_3 shape=(?, 4, 4, 128)

        #将所有的feature map合并成一个2048维向量
        l3 = tf.reshape(l_p_3, [-1, self.w4.get_shape().as_list()[0]])  #reshape to(?,2048)
        l3 = tf.nn.dropout(l3, self.p_keep_conv)

        #后面两层为全连接层
        l4 = tf.nn.relu(tf.matmul(l3, self.w4) + self.b4)
        l4 = tf.nn.dropout(l4, self.p_keep_hidden)

        pyx = tf.matmul(l4, self.w_o) + self.b_o
        #用交叉熵函数的平均值作为损失函数
        cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pyx, labels=Y)) 
        #RMSPro算法最小化目标函数
        train_op = tf.train.RMSPropOptimizer(0.001, 0.9).minimize(cost)     
        predict_op = tf.argmax(pyx, 1)      #返回每个样本的预测结果

        config = tf.ConfigProto(allow_soft_placement=True,log_device_placement=True)
        with tf.Session(config= config) as sess:
            tf.global_variables_initializer().run()         #初始化所有变量
            for i in range(10):                             #训练10次
                training_batch = zip(range(0, len(self.trX), batch_size),\
                                     range(batch_size, len(self.trX)+1, batch_size))
                for start, end in training_batch:           #分批次进行训练
                    sess.run(train_op, feed_dict={X: self.trX[start:end],\
                    Y:self.trY[start:end],self.p_keep_conv: 0.8, self.p_keep_hidden: 0.5})
                if i % 3 == 0:
                    corr = np.mean(np.argmax(self.vaY, axis=1) == sess.run(predict_op,\
                                   feed_dict={X: self.vaX, Y: self.vaY, self.p_keep_conv:1.0,\
                                              self.p_keep_hidden:1.0}))
                    print("Accuracy at step %s on validation set:%s" % (i, corr))

             #最终在测试集上的输出    
            corr_te = np.mean(np.argmax(self.teY, axis=1) == sess.run(predict_op,\
                                   feed_dict={X: self.teX, Y: self.teY, self.p_keep_conv:1.0,\
                                              self.p_keep_hidden:1.0}))

            print("Accuracy on test set : %s " % corr_te)             
#求测试集上的准确率时，上述代码在有GPU的电脑上运行时可能会报显存不足的错误，我尝试改成以下注释部分，
#又会出现警告，DeprecationWarning: elementwise == comparison failed; this will raise an error in the future.
#                               self.p_keep_conv:1.0, self.p_keep_hidden:1.0}))      
#结果显示为     Accuracy on test set : 0.0 
#如果路过的朋友知道如何解决，还请多多指教。

#            test_batch = zip(range(0, len(self.teX), batch_size),\
#                                     range(batch_size, len(self.teX)+1, batch_size))
#            for start, end in test_batch:
#                corr_te = np.mean(np.argmax(self.teY, axis=1) == sess.run(predict_op,\
#                              feed_dict={X: self.teX[start:end], Y: self.teY[start:end],
#                                          self.p_keep_conv:1.0, self.p_keep_hidden:1.0}))
#                print("Accuracy on test set : %s " % corr_te)    


if __name__=="__main__":
    # 1.导入数据集
    start = time.clock() #计算开始时间
    mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
    #mnist.train.images是一个55000*784维的矩阵，mnist.train.labels是一个55000*10维的矩阵
    trX, trY, vaX, vaY, teX, teY = mnist.train.images,mnist.train.labels,\
                                    mnist.validation.images,mnist.validation.labels,\
                                    mnist.test.images, mnist.test.labels
    trX = trX.reshape(-1, 28, 28, 1)        #将每张图片用一个28X28的矩阵表示（55000，28，28，1)
    vaX = vaX.reshape(-1, 28, 28, 1)
    teX = teX.reshape(-1, 28, 28, 1)
    #2 .训练CNN模型
    cnn = CNN(trX, trY, vaX, vaY, teX, teY)
    cnn.fit()
    end = time.clock() #计算程序结束时间

    print("running time is", (end-start)/60,"min")